Секретная Служба Его Величества Бубея Второго разоблачила заговор среди придворных. Теперь необходимо уволить всех явных заговорщиков и подозрительных придворных. Придворный считается «явным заговорщиком» - если существуют явные доказательства его причастности к заговору. Придворный считается «подозрительным», если он был назначен на свою должность кем-то из «явных заговорщиков» или других «подозрительных» придворных. Определите, сколько людей сохранит свои должности при дворе Его Величества.

Совсем недавно появилась в продаже новая компьютерная игра «Морской бой—3». Вася купил себе эту игру и теперь играет в нее в свободное от занятий время. Особенно ему нравится в одной из миссий управлять самолетом. Изначально самолет находится на палубе неподвижного авианосца и готов в любой момент к взлету. Задача игрока в этой миссии состоит в уничтожении \(N\) кораблей противника. После уничтожения всех кораблей самолет должен вернуться обратно на авианосец.

Для простоты будем считать плоской поверхность моря, где располагается авианосец. Введем прямоугольную декартову систему координат и разместим авианосец в начале координат. Каждый из кораблей в начальный момент игры находится в некоторой точке (\(x\), \(y\)), и сразу после начала игры движется равномерно и прямолинейно так, что его вектор скорости равен (\(V_x\), \(V_y\)).

Конструктивные особенности самолета таковы, что он может двигаться с любой скоростью, не превосходящей \(U\). Для того, чтобы сбросить бомбу, которая была специально придумана для этой игры, самолету необходимо находиться непосредственно над кораблем. Корабли считаются точками, т.е. размером кораблей можно пренебречь. Считается также, что самолет может мгновенно взлететь с палубы авианосца, и время падения бомбы на цель равно нулю.

Требуется написать программу, определяющую минимальное время, за которое игрок сможет уничтожить все корабли и возвратить самолет обратно на авианосец.

В недавно открытой раздевалке школы «Интеллектуал» решено поставить такие же шкафчики, как и в уже давно используемых раздевалках, но более новой модификации — состоящие из \(H*W\) ячеек. Напомним, что в каждую ячейку можно поставить ящичек, чтобы хранить в нём свои вещи. Однако новый директор школы запретил ученикам хранить свои вещи вне ящичков, поэтому тем, кому ящички не достались, приходится просить кого-то из владельцев соседних четырёх (или менее, если ячейка находится на границе) ячеек похранить свои вещи у себя. Если же ни у кого из соседей по ячейкам нет ящичков, этот ученик жалуется в администрацию.

Классному руководителю вдруг стало интересно, сколько же существует способов для каждого ученика определить, давать ли ему ящичек, чтобы никто не пожаловался в администрацию.

Количество учеников равно количеству ячеек.

К 2110 году город Флэтбург, являясь одним из крупнейших городов мира, не имеет обходной автомагистрали, что является существенным препятствием для его развития как крупнейшего транспортного центра мирового значения. В связи с этим ещё в 2065 году при разработке Генерального плана развития Флэтбурга была определена необходимость строительства кольцевой автомобильной дороги.

В Генеральном плане также были обозначены требования к этой дороге. Она должна соответствовать статусу кольцевой — иметь форму окружности. Кроме этого, четыре крупные достопримечательности Флэтбурга должны быть в одинаковой транспортной доступности от дороги. Это предполагается обеспечить тем, что они будут находиться на равном расстоянии от неё. Расстоянием от точки расположения достопримечательности до дороги называется наименьшее из расстояний от этой точки до некоторой точки, принадлежащей окружности автодороги.

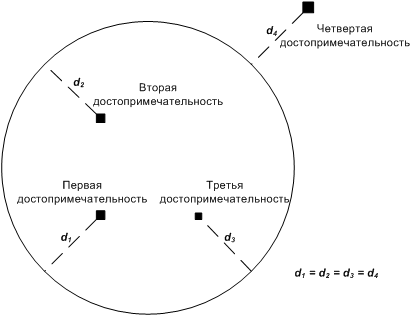
Требуется написать программу, которая вычислит число возможных планов постройки кольцевой автомобильной дороги с соблюдением указанных требований и найдёт такой план, для которого длина дороги будет минимальной. Гарантируется, что хотя бы один план постройки существует.

В наши дни предоставление поверхностей заборов и стен промышленных зданий рекламодателям — уже не оригинальный способ получить дополнительный заработок, а нечто само собой разумеющееся.

Небольшая компания «Домострой» также решила выйти на этот рынок и стала предлагать место для рекламы на своих блоках заборов. Блок представляет собой параллелепипед размером \(1\times1\times L\), на одной из сторон которого есть место для рекламы — пространство размера \(1\times L\), в которое можно вписать ровно \(L\) букв латинского алфавита.

К сожалению, иногда сделки у компании срывались, и заранее подготовленные блоки с рекламой отправлялись на склад. Со временем там скопилось приличное количество блоков различных типов (блоки разных типов отличаются друг от друга только надписью), поэтому было решено использовать их вторично.

Была предложена следующая идея: если поставить несколько блоков друг на друга и закрасить ненужные буквы, то, читая сверху вниз и слева направо, можно будет прочитать какой-нибудь другой текст, как показано на рисунке.

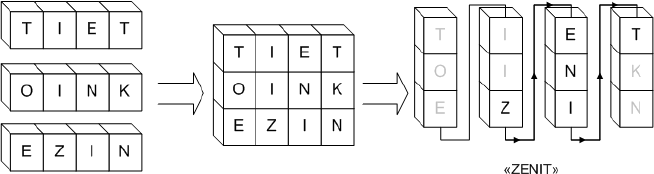
После того, как некоторое число \(K\) блоков, каждый из которых имеет длину \(L\), поставили друг на друга, получилась прямоугольная таблица размером \(K\times L\), в каждой клетке которой находится буква латинского алфавита. Каждый рекламный блок соответствует строке этой таблицы. Теперь содержимое этой таблицы выписывается по столбцам, начиная с самого левого. При этом в каждом столбце буквы выписываются сверху вниз. В случае, изображённом на рисунке, в результате этого процесса получилась бы строка «TOEIIZENITKN». Необходимо, чтобы рекламная надпись, требуемая заказчику, входила в получившуюся строку как подстрока «TOEIIZENITKN».

Требуется написать программу, которая будет определять, какое минимальное количество блоков надо использовать, чтобы получить рекламную надпись, необходимую заказчику. При этом можно считать, что на складе блоков каждого типа неограниченно много.