Перебор с отсечением(22 задач)
Простые задачи на перебор(43 задач)
Гамильтонов цикл(2 задач)
После своего первого контакта с землянами обитатели планеты Пандора решили всё-таки перенять часть земных технологий. В частности, они предприняли попытку приспособить к особенностям своей планеты систему железнодорожного сообщения.
Построенная пандорианцами железная дорога представляет собой прямой отрезок, проходящий в непосредственной близости от N красивейших водопадов. Паровозик, который планируется запустить по этой дороге, будет без остановок проезжать весь маршрут, преодолевая участки между водопадами за строго определённое время.
Так как жители Пандоры очень трепетно относятся к красотам своей природы, они не хотят упускать ни малейшей возможности полюбоваться водопадами, искрящимися в дневном свете. Грамотно составлять расписания пандорианцы ещё не научились, и теперь они обратились за помощью к вам, участникам олимпиады по программированию.
Помогите обитателям Пандоры определить, в какое время дня паровозик должен проехать рядом с первым водопадом, чтобы пассажиры смогли увидеть все водопады на пути в дневное время, при этом не обязательно в один и тот же день. Водопад виден лишь в момент проезда паровозика мимо него, но, как известно, пандорианские водопады настолько впечатляющие, что и за мгновение можно сполна насладиться любым из них.
В первой строке через пробел вводятся два натуральных числа: количество часов в одних сутках ( H ) и минут в одном часу ( M ) на Пандоре ( 1 ≤ H , M ≤ 500 ).
Следующая строка содержит четыре целых числа, описывающих время начала ( H s , M s ) и конца ( H f , M f ) светового дня ( 0 ≤ H s , H f < H ; 0 ≤ M s , M f < M ). При этом либо H s < H f , либо H s = H f и M s < M f (гарантируется, что день начинается раньше, чем заканчивается). Если паровозик проезжает мимо водопада ровно в H s часов M s минут или ровно в H f часов M f минут, то считается, что он проехал мимо водопада днём.
Третья строка содержит одно натуральное число N — количество водопадов, рядом с которыми проезжает паровозик ( 1 ≤ N ≤ 100 000 ).
В следующих N - 1 строках вводятся по 2 целых числа H i и M i , описывающих продолжительность временных интервалов для проезда между соседними водопадами: H 1 , M 1 — время в пути между первым и вторым водопадами, H 2 , M 2 — между вторым и третьим и так далее. Гарантируется, что время, затрачиваемое на дорогу между любыми двумя соседними водопадами, строго положительно, не превосходит одних пандорианских суток и записано корректно: 0 ≤ H i ≤ H , 0 ≤ M i < M .
Если составить подходящее расписание невозможно, то в качестве ответа выведите одно слово « Impossible » (без кавычек). Иначе выведите два числа H 0 и M 0 , разделённые пробелом, описывающие любое подходящее время проезда паровозика рядом с первым водопадом.
Тесты к этой задаче состоят из четырех групп.
Тестирование на тестах каждой группы производится только в случае прохождения всех тестов из всех предыдущих групп.
24 60 8 0 22 0 6 6 0 21 0 19 0 12 0 10 0
12 0
24 60 8 17 20 10 2 11 59
Impossible
Поблизости от столицы Флатландии одна компания решила построить коттеджный поселок. Строительная компания, которая занимается возведением коттеджей, решила раскрасить некоторые коттеджи в розовый цвет, а остальные - в голубой. Но они не могут решить какой коттедж раскрасить в какой цвет.
Директор компании утверждает, что раскраска симпатичная, если есть хотя бы один розовый коттедж, хотя бы один голубой коттедж, и можно провести такую прямую, что все розовые коттеджи окажутся с одной стороны от нее, я голубые - с другой стороны (при этом на самой прямой коттеджей быть не должно). На это главный дизайнер возразил, что есть несколько способов сделать симпатичную раскраску.
Помогите им определить, сколько существует различных симпатичных раскрасок.
Первая строка входного файла input.txt содержит число n - количество коттеджей (1 ≤ n ≤ 300) . Следующие n строк содержат координаты коттеджей, каждая строка содержит два целых числа x i и y i ( - 10 4 ≤ x i , y i ≤ 10 4 ) .
Выведите в файл output.txt одно число - количество симпатичных раскрасок коттеджного поселка.
Возможные раскраски приведены на следующем рисунке.
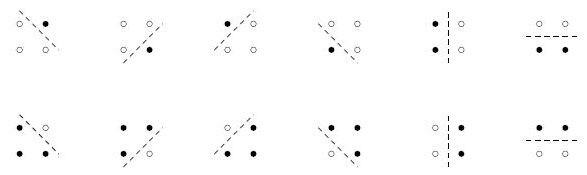
4 0 0 1 0 1 1 0 1
12
Девочка Катя любит разные игры со словами. Недавно она придумала новую игру. Увидев где-либо написанное слово, она пытается придумать предложение, содержащее это слово в себе. Буквы увиденного слова должны идти в предложении по порядку, но не обязательно подряд. Например, увидев слово "LTIBE", она придумывает предложение "LET IT BE". Разумеется, Катя ищет кратчайшее предложение.
Ваша задача помочь Кате, автоматизировав игру.
В первой строке содержится увиденное Катей слово. Слово состоит из заглавных латинских букв. Его длина не менее 1 символа и не более 500. Во второй строке входного файла записано целое число N (1 ≤ N ≤ 500) — количество слов в словарном запасе Кати. Далее в N строках записаны слова. Слова состоят из заглавных латинских букв, содержат не менее 1 и не более 50 букв. Слова в наборе могут совпадать. В искомом предложении слово может использоваться любое количество раз, главное, чтобы оно содержалось в списке.
Выведите искомое предложение. Слова в предложении разделяйте пробелами. Длиной предложения называется количество символов (включая пробелы) использующихся при его записи. Переведите в нижний регистр те символы, которые образуют заданное слово. Если решений несколько, выведите любое. Если решения не существует, выведите в выходной файл символ "*".
LTIBE 5 IT THE LET BEE BE
lEt iT be
Феоктист Всеволодович — преподаватель физкультуры старой закалки, глубоко убеждённый, что в начале каждого урока школьников необходимо построить по росту. Для этого он сначала просит школьников построиться самостоятельно, после чего последовательно меняет местами произвольную пару стоящих рядом учеников, пока шеренга не примет желанный вид.
Всего на урок пришло \(N\) детей, изначально построившихся таким образом, что рост стоящего на позиции \(i\) равен \(h_i\) (используется нумерация c \(1\)). Можно считать, что все числа \(h_i\) различны и лежат в диапазоне от 1 до \(N\). Шеренга считается упорядоченной, если на первой позиции стоит школьник ростом один, на второй позиции стоит школьник ростом два и так далее.
Феоктист Всеволодович получает большое удовольствие от процесса упорядочивания школьников, поэтому он всегда выбирает наиболее длинную последовательность обменов. С другой стороны, он не хочет чтобы ученики догадались о том, что он умышленно затягивает построение, поэтому никогда не делает заведомо бессмысленных обменов. А именно, преподаватель никогда не меняет местами школьников на позициях \(i\) и \(j\), если \(h_i < h_j\) . Очевидно, что данное ограничение делает процесс сортировки шеренги по росту конечным.
Староста Саша очень любит играть в волейбол и прекрасно понимает, что чем дольше преподаватель будет расставлять всех по местам, тем меньше времени останется для игры. Ученики уже построились некоторым образом, а Феоктист Всеволодович вышел поговорить по телефону, так что Саша может успеть поменять местами ровно двух школьников, необязательно стоящих рядом в шеренге. Разумеется, он хочет сделать это таким образом, чтобы преподаватель как можно быстрее закончил упорядочивать шеренгу (Саша давно уже раскусил, как именно действует Феоктист Всеволодович). С информатикой у старосты всегда были определённые проблемы, поэтому ему требуется ваша помощь.
В первой строке ввода содержится единственное число N — количество школьников на уроке (\(1 \le N \le 1 000 000\)).
Во второй строке записано \(N\) различных целых чисел \(h_i\) (\(1 \le h_i \le N\)). \(i\)-е число соответствует росту школьника стоящего на \(i\)-й позиции
Выведите два числа — номера позиций школьников, которым необходимо поменяться местами, чтобы минимизировать количество действий преподавателя. Если таких пар несколько, то выведите любую из них. Если никому меняться местами не нужно, выведите -1 -1
В первом примере из условия после Сашиной перестановки, получится последовательность {2, 1, 3, 5, 4}, и тренер сможет сделать всего два обмена, перед тем как последовательность станет упорядоченной (например, он может поменять местами 1-го и 2-го школьника, а затем 4-го и 5-го). Если Саша поменяет местами двух других школьников, тренер затем сможет сделать три или более обменов.
Тесты к этой задаче состоят из одиннадцати групп. Баллы за каждую группу тестов ставятся только при прохождении всех тестов группы и всех тестов предыдущих групп.

5 2 4 3 5 1
2 5
4 1 2 3 4
-1 -1
10 2 3 7 1 5 10 4 6 9 8
3 7
Андрей работает судьей на чемпионате по гипершашкам. В каждой игре в гипершашки участвует три игрока. По ходу игры каждый из игроков набирает некоторое положительное целое число баллов. Если после окончания игры первый игрок набрал \(a\) баллов, второй — \(b\), а третий \(c\), то говорят, что игра закончилась со счетом \(a:b:c\).
Андрей знает, что правила игры гипершашек устроены таким образом, что в результате игры баллы любых двух игроков различаются не более чем в \(k\) раз.
После матча Андрей показывает его результат, размещая три карточки с очками игроков на специальном табло. Для этого у него есть набор из n карточек, на которых написаны числа \(x_1, x_2, …, x_n\). Чтобы выяснить, насколько он готов к чемпионату, Андрей хочет понять, сколько различных вариантов счета он сможет показать на табло, используя имеющиеся карточки.
Требуется написать программу, которая по числу \(k\) и значениям чисел на карточках, которые имеются у Андрея, определяет количество различных вариантов счета, которые Андрей может показать на табло.
Первая строка входного файла содержит два целых числа: \(n\) и \(k (3 \le n \le 100 000, 1 \le k \le 10^9\) ).
Вторая строка входного файла содержит \(n\) целых чисел \(x_1, x_2, …, x_n (1 \le x_i \le 10^9 )\).
Выходной файл должен содержать одно целое число — искомое количество различных вариантов счета.
В приведенном примере Андрей сможет показать следующие варианты счета: 1:1:2, 1:2:1, 2:1:1, 1:2:2, 2:1:2, 2:2:1, 2:2:3, 2:3:2, 3:2:2. Другие тройки чисел, которые можно составить с использованием имеющихся карточек, не удовлетворяют заданному условию, что баллы любых двух игроков различаются не более чем в \(k\) = 2 раза.
В этой задаче четыре подзадачи. Баллы за подзадачу начисляются только в случае, если все тесты для данной подзадачи пройдены.
\(3 \le n \le 100 000, k = 1, 1 \le x_i \le 100 000\)
\(3 \le n \le 100, k \le 100, 1 \le x_i \le 100\)
\(3 \le n \le 100 000, k \le 10^9 \le x_i \le 10^9\), все \(x_i\) различны
\(3 \le n \le 100 000, k \le 10^9 \le x_i \le 10^9\)
5 2 1 1 2 2 3
9