Вводятся 4 числа: a, b, c и d.
Найдите все целые решения уравнения ax3 + bx2 + cx + d = 0 на отрезке [0,1000] и выведите их в порядке убывания. Если на данном отрезке нет ни одного решения, то ничего выводить не нужно.
Вводятся 5 чисел: a, b, c, d и e.
Найдите все целые решения уравнения ( ax3 + bx2 + cx + d ) / ( x - e ) = 0 на отрезке [0,1000] и выведите их количество.
2 4 9 1 5
0
В саду растут деревья. У каждого есть цена и длина. Чтобы построить забор какой-то длины L, нужно срубить деревьев с суммарной длиной L или больше. Нужно, срубив некоторые деревья, построить забор вокруг оставшихся. При этом нужно потратить как можно меньше денег. Если таких способов несколько, нужно выбрать тот, в котором деревьев рубится меньше. Если и таких несколько, выведите любой. Деревья считаются имеющими нулевой радиус.
Во входном файле записано число деревьев N (2 <= N <= 14), а затем каждое дерево описано четырьмя числами xi, yi, vi, li - координаты (целые от -10000 до 10000), цена и длина (от 0 до 10000).
В выходной файл выведите номера деревьев, которые необходимо срубить, а также излишек срубленного материала. Формат выходных данных - см. примеры выходных файлов.
5 0 0 1000 11 0 3 1000 11 3 0 1000 11 3 3 1000 11 1 1 100 12
Cut these trees: 5 Extra wood: 0.00
2 100 100 100 100 0 1 100 100
Cut these trees: 1 Extra wood: 100.00
Женя получил письмо от Леши со словесным описанием схемы метро в его городе. Метро содержит одну кольцевую линию. Каждая из остальных линий пересекается с кольцевой не более, чем в двух местах, причем в точках пересечения организованы пересадочные станции. В одном месте кольцевую линию могут пересекать сразу несколько линий, имеющих общую пересадочную станцию.
Кроме этих пересадочных станций каждая из линий имеет не более одной пересадочной станции для перехода на другие, отличные от кольцевой, линии. На такой станции также может быть организована пересадка сразу на несколько линий.
Для каждой пересадочной станции Леша описал, какие линии на ней пересекаются, и указал порядок расположения пересадочных станций на кольцевой линии. Он утверждает, что все линии расположены на одной глубине и других пересечений, помимо пересадочных узлов, не имеют. Чтобы проверить это утверждение, Женя стал по словесному описанию рисовать схему метро, но у него не получилось.
Помогите Жене написать программу, которая будет проверять, действительно ли может существовать схема метро, соответствующая полученному описанию.
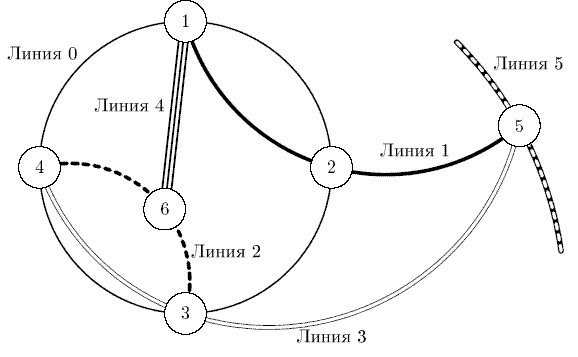
На рисунке приведена возможная схема метро, соответствующая второму примеру.
В первой строке вводится число k – количество линий метро в городе ( 1
k10). Все линии пронумерованы от 0 до k - 1, кольцевая линия имеет номер 0. Во второй строке записано число n – количество пересадочных станций. Каждая из следующих n строк описывает линии, пересекающиеся на соответствующей пересадочной станции, причем сначала следуют описания пересадочных станций, расположенных на кольцевой линии, в порядке их расположения на ней. Описание каждого узла начинается с количества пересекающихся в нем линий, затем следуют номера линий.
Выведите слово YES, если по описанию можно построить схему метро, и NO в противном случае.
4 6 2 0 1 2 0 2 2 0 3 2 0 1 2 0 2 2 0 3
NO
6 6 3 0 1 4 2 0 1 3 0 2 3 3 0 2 3 3 1 3 5 2 2 4
YES
Петя нарисовал на бумаге n кружков и соединил некоторые пары кружков линиями. После этого он раскрасил каждый кружок в один из трех цветов – красный, синий или зеленый.
Теперь Петя хочет изменить их раскраску. А именно – он хочет перекрасить каждый кружок в некоторый другой цвет так, чтобы никакие два кружка одного цвета не были соединены линией. При этом он хочет обязательно перекрасить каждый кружок, а перекрашивать кружок в тот же цвет, в который он был раскрашен исходно, не разрешается.
Помогите Пете решить, в какие цвета следует перекрасить кружки, чтобы выполнялось указанное условие.
В первой строке вводятся два целых числа n и m – количество кружков и количество линий, которые нарисовал Петя, соответственно ( 1n1 000, 0m20 000).
Следующая строка содержит n символов из множества {'R', 'G', 'B'} – i-й из этих символов означает цвет, в который раскрашен i-й кружок ('R' – красный, 'G' – зеленый, 'B' – синий).
Далее в m строках задается по два целых числа – пары кружков, соединенных отрезками.
Выведите одну строку, состоящую из n символов из множества {'R', 'G', 'B'} – цвета кружков после перекраски. Если решений несколько, выведите любое.
Если решения не существует, выведите слово "Impossible''.
4 5 RRRG 1 3 1 4 3 4 2 4 2 3
GGBR
4 5 RGRR 1 3 1 4 3 4 2 4 2 3
Impossible