Натуральные числа записаны в (бесконечную) таблицу, как показано на рисунке.

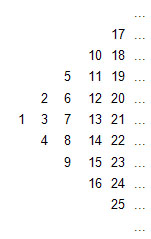
Требуется по заданному числу вывести всех его соседей (числа, записанные в клетках сверху, справа, слева и снизу, если таковые имеются)

Возьмем произвольное слово и проделаем с ним следующую операцию: поменяем местами его первую согласную букву с последней согласной буквой, вторую согласную букву с предпоследней согласной буквой и т.д. Если после этой операции мы вновь получим исходное слово, то будем называть такое слово негласным палиндромом. Например, слова sos, rare, rotor, gong, karaoke являются негласными палиндромами.

Вам требуется написать программу, которая по данному слову определяет, является ли оно негласным палиндромом.

Требуется определить, является ли данный год високосным. (Напомним, что год является високосным, если его номер кратен 4, но не кратен 100, а также если он кратен 400.)

В каждую крайнюю клетку квадратной доски поставили по фишке. Могло ли оказаться, что выставлено ровно \(k\) фишек? (Например, если доска \(2 \times 2\), то выставлено \(4\) фишки, а если \(6 \times 6\) - то \(20\)).

Решить в целых числах уравнение ax + b = 0.