Строки(121 задач)
Целые числа(112 задач)
Битовые операции(28 задач)
Логический тип(3 задач)
Структуры(18 задач)
Вещественные числа(33 задач)
Множества(16 задач)
Словари(21 задач)
Даны три строки, состоящие из строчных латинских букв. С этими строками можно производить следующие операции: либо заменить один символ строки на два таких же символа (например, заменить символ «a» на «aa»), либо, наоборот, заменить два подряд идущих одинаковых символа на один такой же символ.
Необходимо при помощи этих операций сделать все три строки равными какой-то другой общей строке S либо определить, что это сделать невозможно. При этом нужно минимизировать общее количество операций.
Программа получает на вход три строки, состоящие из строчных букв латинского алфавита. Длина каждой строки не превышает 100 символов.
Если при помощи указанных операций возможно сделать все три строки равными, выведите такую строку S , что суммарное число операций, необходимых для преобразования всех трёх данных строк к строке S , будет минимальным. Если этого сделать нельзя, программа должна вывести одно слово IMPOSSIBLE (заглавными буквами).
Решение, которое выводит правильный ответ только на тестах из условия и тех тестах, на которых ответом является слово IMPOSSIBLE, будет оцениваться в 0 баллов.
aaaza aazzaa azzza
aazza
xy xxyy yx
IMPOSSIBLE
В некотором королевстве есть \(N\) провинций. Король пожелал объединить все их под своей самодержавной властью. Естественно, чтобы никто не догадался об этих планах, он будет это делать поэтапно, а именно: раз в год он будет объединять какие-то две провинции в одну. Чтобы жителям обеих провинций не было обидно, новому территориальному образованию будет присвоено новое название, которое будет отличаться от обоих старых названий. Естественно, это потребует выпуска новых паспортов для жителей обеих провинций.
Очевидно, что если в первой провинции \(p_i\) жителей, а во второй – \(p_j\) жителей, то для них надо выпустить \(p_i + p_j\) новых паспортов.
На следующий год король объединяет еще какие-то две провинции. И так далее, до тех пор пока вся территория королевства не будет объединена в одну большую «провинцию». Определите, какое наименьшее количество новых паспортов придется выпустить, если король будет объединять провинции оптимально с этой точки зрения.
В первой строке вводится число \(N\) (натуральное, не превышает \(10^5\)) – количество провинций. Затем вводится \(N\) чисел – количество жителей каждой провинции (натуральное, не превосходит \(10^9\)). Гарантируется, что изначально в королевстве хотя бы две провинции.
Выведите единственное число – количество новых паспортов, которые придется выпустить.
2 2 6
8
3 6 2 4
18
Вася придумал свой собственный алфавит, в котором \(N\) символов. Теперь он хочет составить c с помощью этого алфавита все слова, состоящие ровно из \(K\) букв, причём ни одно слово не может начинаться с первой буквы алфавита и не может заканчиваться на последнюю букву алфавита. Помогите Васе определить, сколько он сможет составить таких слов.
Входная строка содержит два числа, разделённых пробелом: число символов в алфавите \(N\) и длину слов \(K\) (\(0\) < \(N, K\) <= \(10\)).
Программа должна вывести единственное число - количество слов длиной \(K\) в алфавите мощностью \(N\), таких что ни одно слово не начинается с первой буквы алфавита и не заканчивается на последнюю букву алфавита.
4 1
2
Английский фермер тщательно следит за своим газоном, в котором в каждой точке с целыми координатами растет один пучок травы. Как-то фермер воспользовался газонокосилкой и постриг траву на некотором прямоугольном участке газона. Стороны этого участка параллельны осям координат, а две противоположные вершины расположены в точках \((x_1, y_1)\) и \((x_2, y_2)\). Следует отметить, что пучки травы, находящиеся на границе этого прямоугольника, также были пострижены.
Для полива газона фермер установил в точке с координатами \((x_3, y_3)\) дождевальную установку, радиус действия которой равен \(r\). Таким образом, установка начала поливать все пучки, расстояние от которых до точки \((x_3, y_3)\) не превышало \(r\).
Фермера заинтересовал следующий вопрос: сколько пучков травы оказалось и пострижено, и полито в этот день? Требуется написать программу, которая позволит дать ответ на вопрос фермера.
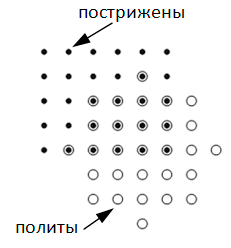
Первая входная строка содержит четыре целых числа: \(x_1, y_1, x_2, y_2 (−100 000 \le x_1 < x_2 \le 100 000; −100 000 \le y_1 < y_2 \le 100 000)\). Во второй входной строке записаны три целых числа: \(x_3, y_3, r (−100 000 \le x_3, y_3 \le 100 000; 1 \le r \le 100 000)\).
Необходимо вывести одно целое число – число пучков травы, которые были и пострижены, и политы.
Все координаты не превосходят 1000. Решение оценивается в 30 баллов.
Радиус и стороны прямоугольника не превосходят 10000. Решение оценивается в 30 баллов.
Дополнительные ограничения отсутствуют. Решение оценивается в 40 баллов.
0 0 5 4 4 0 3
14
-100 -100 100 100 0 0 50
7845
0 0 10 10 100 100 5
0
Как известно, в шахматах горизонтальные строки обозначаются цифрами от 1 до 8, считая от расположения белых фигур, стоящих внизу доски, а вертикальные столбцы – буквами латинского алфавита: A, B, C, D, E, F, G, H.
На шахматной доске в клетке с заданными координатами находиться конь. Для клетки А1 после первого хода возможно перемещение коня на клетку С2 или В3.
Требуется написать программу, которая определяет координаты всех клеток, куда можно пойти конём первым ходом.
В единственной входной строке записано обозначение исходной позиции коня на шахматной доске.
В единственной строке должны быть записаны через пробел обозначения всех клеток, в которые может переместиться конь после первого хода. Клетки выводятся в следующем порядке: вначале клетки первого ряда слева – направо, далее клетки второго ряда и т.д.
A1
C2 B3