--->
102 задач
<---
Источники
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
128 megabytes
Для заданного натурального N найти последнюю ненулевую цифру числа N!.
Входные данные
Входной файл содержит число N (0 ≤ N ≤ 1 000 000).
Выходные данные
Выходной файл должен содержать одну цифру — последнюю ненулевую.
Примеры
Входные данные
8
Выходные данные
2
Входные данные
10
Выходные данные
8
#111986
Темы:
[Цикл for]
Источники:
[
Личные олимпиады,
Всероссийская олимпиада школьников,
Муниципальный этап,
Московская область,
Очный этап,
2013,
7-9 классы,
Олимпийский огонь
]
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes
В одном известном всем городе скоро стартуют Зимние Олимпийские игры. В связи с этим организаторы игр решили провести эстафету Олимпийского огня — самую продолжительную и масштабную в истории Олимпийских игр. Эстафета состоит из \(N\) этапов, каждый длиной \(a_i\) километров (\(1 \le i \le N\)). У организаторов имеется большое количество олимпийских факелов, каждый из которых может непрерывно гореть на протяжении \(K\) километров забега. По правилам эстафеты каждый факел используется только один раз. В начале каждого этапа участникам эстафеты выдаётся некоторое число факелов, такое, чтобы олимпийский огонь удалось донести до конца этапа. По окончании этапа все использованные (полностью или частично) факелы передаются в дар своим факелоносцам.
Напишите программу, которая по известной схеме эстафеты олимпийского огня, определяет необходимое суммарное количество факелов для проведения эстафеты.
Входные данные
В первой строке заданы два натуральных числа \(N\) и \(K\) (\(N \le 100, K \le 10^6\) ).
Во второй строке заданы \(N\) натуральных чисел \(a_i (a_i \le 10^6 )\).
Выходные данные
В первой строке выведите одно натуральное число \(F\) — количество факелов, которое понадобится организаторам для проведения эстафеты олимпийского огня.
Примечания
В данной задаче баллы за каждый тест начисляются независимо от прохождения остальных тестов и суммируются.
Примеры
Входные данные
4 3 3 5 4 1
Выходные данные
6
Входные данные
10 1 1 2 3 4 5 6 7 8 9 10
Выходные данные
55
#111987
Темы:
[Цикл for]
Источники:
[
Личные олимпиады,
Всероссийская олимпиада школьников,
Муниципальный этап,
Московская область,
Очный этап,
2013,
7-9 классы,
Шахматные клетки
]
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes
Недавно Петя услышал на шахматном кружке о мегашахматах.
Поле для мегашахмат — это разделённый на клетки прямоугольник, в котором каждый горизонтальный ряд клеток имеет свою высоту, а каждый вертикальный столбец — свою ширину. Всего на поле n рядов и m столбцов клеток, высота i-го ряда составляет ai сантиметров, а ширина j-го столбца — bj сантиметров. Столбцы нумеруются слева направо, а строки — снизу вверх. Клетки покрашены в чёрный и белый цвета в шахматном порядке, левая нижняя клетка поля черная. Это значит, что соседи каждой клетки по вертикали и горизонтали отличаются от нее по цвету.
Пете стало очень интересно, какую площадь в квадратных сантиметрах занимают чёрные и белые клетки. Напишите программу, которая вычислит искомые площади.
Входные данные
В первой строке вводятся два целых числа n и m — количества рядов и столбцов клеток на поле для мегашахмат (1 ≤ n, m ≤ 105).
Во второй строке вводится n целых чисел ai — высоты рядов клеток в сантиметрах (1 ≤ ai ≤ 100).
В третьей строке вводится m целых чисел bj — ширины столбцов клеток в сантиметрах (1 ≤ bj ≤ 100).
Выходные данные
Выведите два числа в одной строке: площадь всех чёрных клеток и площадь всех белых клеток в квадратных сантиметрах на поле.
Примеры тестов
Входные данные
8 8
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
Выходные данные
32 32
Входные данные
2 3
3 2
3 2 1
Выходные данные
16 14
Примечание
Второй тест из условия соответствует рисунку.
Тесты к этой задаче состоят из трех групп. Если решение не проходит какую-либо группу тестов, следующие группы не проверяются.
- Тесты 1 – 2. Тесты из условия, оцениваются в ноль баллов.
- Тесты 3 – 20. В тестах этой группы 1 ≤ n, m ≤ 103, 1 ≤ ai, bi ≤ 10. Эта группа оценивается в 40 баллов, баллы ставятся только при прохождении всех тестов группы.
- Тесты 21 – 32. В тестах этой группы дополнительные ограничения отсутствуют. Прохождение тестов из этой группы оценивается из 60 баллов, баллы начисляются за каждый тест независимо от прохождения остальных тестов и суммируются.
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes
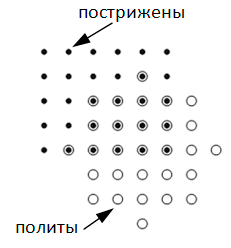
Английский фермер тщательно следит за своим газоном, в котором в каждой точке с целыми координатами растет один пучок травы. Как-то фермер воспользовался газонокосилкой и постриг траву на некотором прямоугольном участке газона. Стороны этого участка параллельны осям координат, а две противоположные вершины расположены в точках \((x_1, y_1)\) и \((x_2, y_2)\). Следует отметить, что пучки травы, находящиеся на границе этого прямоугольника, также были пострижены.
Для полива газона фермер установил в точке с координатами \((x_3, y_3)\) дождевальную установку, радиус действия которой равен \(r\). Таким образом, установка начала поливать все пучки, расстояние от которых до точки \((x_3, y_3)\) не превышало \(r\).
Фермера заинтересовал следующий вопрос: сколько пучков травы оказалось и пострижено, и полито в этот день? Требуется написать программу, которая позволит дать ответ на вопрос фермера.
Входные данные
Первая входная строка содержит четыре целых числа: \(x_1, y_1, x_2, y_2 (−100 000 \le x_1 < x_2 \le 100 000; −100 000 \le y_1 < y_2 \le 100 000)\). Во второй входной строке записаны три целых числа: \(x_3, y_3, r (−100 000 \le x_3, y_3 \le 100 000; 1 \le r \le 100 000)\).
Выходные данные
Необходимо вывести одно целое число – число пучков травы, которые были и пострижены, и политы.
Подзадача 1
Все координаты не превосходят 1000. Решение оценивается в 30 баллов.
Подзадача 2
Радиус и стороны прямоугольника не превосходят 10000. Решение оценивается в 30 баллов.
Подзадача 3
Дополнительные ограничения отсутствуют. Решение оценивается в 40 баллов.
Примеры
Входные данные
0 0 5 4 4 0 3
Выходные данные
14
Входные данные
-100 -100 100 100 0 0 50
Выходные данные
7845
Входные данные
0 0 10 10 100 100 5
Выходные данные
0
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes
Как известно, в шахматах горизонтальные строки обозначаются цифрами от 1 до 8, считая от расположения белых фигур, стоящих внизу доски, а вертикальные столбцы – буквами латинского алфавита: A, B, C, D, E, F, G, H.
На шахматной доске в клетке с заданными координатами находиться конь. Для клетки А1 после первого хода возможно перемещение коня на клетку С2 или В3.
Требуется написать программу, которая определяет координаты всех клеток, куда можно пойти конём первым ходом.
Входные данные
В единственной входной строке записано обозначение исходной позиции коня на шахматной доске.
Выходные данные
В единственной строке должны быть записаны через пробел обозначения всех клеток, в которые может переместиться конь после первого хода. Клетки выводятся в следующем порядке: вначале клетки первого ряда слева – направо, далее клетки второго ряда и т.д.
Примеры
Входные данные
A1
Выходные данные
C2 B3
Выбрано
:
|