Вася записывает в клетки квадратной таблицы NxN натуральные числа по порядку, сначала заполняя первую строку слева направо, затем вторую и т.д. (см. рисунок слева). Петя заполняет такую же таблицу, расставляя числа сначала в первый столбец сверху вниз, затем во второй столбец и т.д.

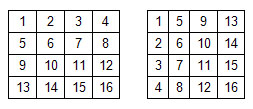
При этом оказалось, что некоторые числа и Вася, и Петя записали в одну и ту же клетку (например, число 6 записано во вторую строку второго столбца обеих таблиц).

Вам требуется написать программу, выводящую  все числа, которые в обеих таблицах записаны в одних и тех же клетках.

Требуется сравнить два 100-значных числа.

Сколько понадобится парт, чтобы рассадить \(A\) школьников, если за одну парту можно посадить одного или двух человек? За каждой партой должен сидеть хотя бы один человек. Укажите все варианты.

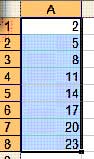Если в Microsoft Excel выделить две соседние клетки с числами, а потом “потянуть” за правый нижний уголок мышью, то следующие клетки заполнятся числами, образуя арифметическую прогрессию.