--->
112 задач
<---
Источники
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes
Назовем число палиндромом, если оно не меняется при перестановке его цифр в обратном порядке. Напишите программу, которая по заданному числу K выводит количество натуральных палиндромов, не превосходящих K.
Входные данные
Задано единственное число K (\(1 \leq K \leq 100 000\)).
Выходные данные
Необходимо вывести количество натуральных палиндромов, не превосходящих K.
Примеры
Входные данные
1
Выходные данные
1
Входные данные
100
Выходные данные
18
#235
Темы:
[Целые числа]
[Условный оператор (if)]
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes
Решите в целых числах уравнение:
\(\sqrt{ax+b} = c\),
a, b, c – данные целые числа: найдите все решения или сообщите, что решений в целых числах нет.
Входные данные
Вводятся три числа a, b и c, разделенные пробелами.
Выходные данные
Программа должна вывести все решения уравнения в порядке возрастания, либо NO SOLUTION (заглавными буквами), если решений нет. Если решений бесконечно много, вывести MANY SOLUTIONS.
Примеры
Входные данные
1 0 0
Выходные данные
0
Входные данные
1 2 -3
Выходные данные
NO SOLUTION
#236
Темы:
[Целые числа]
[Условный оператор (if)]
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes
Натуральные числа записаны в (бесконечную) таблицу, как показано на рисунке.
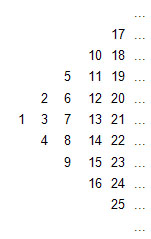
Требуется по заданному числу вывести всех его соседей (числа, записанные в клетках сверху, справа, слева и снизу, если таковые имеются)
Входные данные
Вводится одно натуральное число, не превосходящее \(10^9\).
Выходные данные
Программа должна вывести все числа, записанные в соседних клетках с данным, в порядке возрастания. Числа должны разделяться пробелом.
Примеры
Входные данные
1
Выходные данные
3
Входные данные
7
Выходные данные
3 6 8 13
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes
Требуется определить, является ли данный год високосным. (Напомним, что год является високосным, если его номер кратен 4, но не кратен 100, а также если он кратен 400.)
Входные данные
Вводится единственное число - номер года (целое, положительное, не превышает 30000).
Выходные данные
Требуется вывести слово YES, если год является високосным и NO - в противном случае.
Примеры
Входные данные
2007
Выходные данные
NO
Входные данные
2000
Выходные данные
YES
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes
В каждую крайнюю клетку квадратной доски поставили по фишке. Могло ли оказаться, что выставлено ровно \(k\) фишек? (Например, если доска \(2 \times 2\), то выставлено \(4\) фишки, а если \(6 \times 6\) - то \(20\)).
Входные данные
Вводится одно натуральное число \(k\), не превосходящее \(30\,000\)
Выходные данные
Программа должна вывести слово YES, если существует такой размер доски, на который будет выставлено ровно (не больше, и не меньше) \(k\) фишек, в противном случае - вывести слово NO.
Примеры
Входные данные
20
Выходные данные
YES
Входные данные
13
Выходные данные
NO
Выбрано
:
|