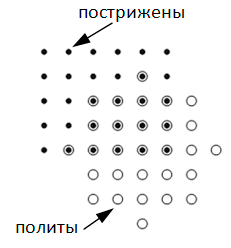
Английский фермер тщательно следит за своим газоном, в котором в каждой точке с целыми координатами растет один пучок травы. Как-то фермер воспользовался газонокосилкой и постриг траву на некотором прямоугольном участке газона. Стороны этого участка параллельны осям координат, а две противоположные вершины расположены в точках \((x_1, y_1)\) и \((x_2, y_2)\). Следует отметить, что пучки травы, находящиеся на границе этого прямоугольника, также были пострижены.

Для полива газона фермер установил в точке с координатами \((x_3, y_3)\) дождевальную установку, радиус действия которой равен \(r\). Таким образом, установка начала поливать все пучки, расстояние от которых до точки \((x_3, y_3)\) не превышало \(r\).

Фермера заинтересовал следующий вопрос: сколько пучков травы оказалось и пострижено, и полито в этот день? Требуется написать программу, которая позволит дать ответ на вопрос фермера.

Как известно, в шахматах горизонтальные строки обозначаются цифрами от 1 до 8, считая от расположения белых фигур, стоящих внизу доски, а вертикальные столбцы – буквами латинского алфавита: A, B, C, D, E, F, G, H.

На шахматной доске в клетке с заданными координатами находиться конь. Для клетки А1 после первого хода возможно перемещение коня на клетку С2 или В3.

Требуется написать программу, которая определяет координаты всех клеток, куда можно пойти конём первым ходом.

Как известно, в шахматах горизонтальные строки обозначаются цифрами от 1 до 8, считая от расположения белых фигур, стоящих внизу доски, а вертикальные столбцы – буквами латинского алфавита: A, B, C, D, E, F, G, H.

На шахматной доске в клетке с заданными координатами находиться конь. Сначала делается первый ход конём, а затем – второй ход. Например, для клетки А1 после первого хода возможно перемещение коня на клетку С2 или В3, а после второго хода – на клетки А1, Е1, А3, Е3, В4, D4.

Требуется написать программу, которая определяет координаты всех клеток, куда можно прийти конём за два хода.

В конструкторском бюро проектируют планетоход для исследования поверхности планеты Марс. Исследования должны проводиться на прямоугольной области планеты без препятствий внутри неё. Эта область разделена на единичные квадраты и имеет размеры \(M \times N\), где \(M\) – высота прямоугольника, а \(N\) – его ширина.

Планируется, что планетоход должен работать по следующей программе. Вначале он садится в северо-западном углу заданной области в направлении на восток. После этого планетоход начинает обход и исследование выбранной области, двигаясь по спирали по часовой стрелке. При этом спираль постепенно «закручивается» вовнутрь, захватывая постепенно все клетки прямоугольника. Исследование заканчивается, когда пройдены все клетки (после очередного поворота планетохода).

Требуется написать программу, которая для заданных \(M\) и \(N\) (\(1 \le M, N \le 32767\)) определяет количество поворотов, которые должен выполнить планетоход в процессе исследования области.

Числа в позиционной троично-симметричной системе счисления записываются с использованием трех символов: +, –, 0. Например, такими числами являются, например,

"+ + 0 – 0", "– – 0 +", "– – –".

Эти числа переводятся в десятичную систему как:

   а) + + 0 – 0 = 1*\(3^4\) + 1*\(3^3\) + 0*\(3^2\) – 1*\(3^1\) + 0*\(3^0\)

   б) – – 0 + = – 1*\(3^3\) – 1*\(3^2\) + 0*\(3^1\) + 1*\(3^0\)

   в) – – – = – 1*\(3^2\) – 1*\(3^1\) – 1*\(3^0\)

Над числами в позиционной троично-симметричной системе счисления можно выполнять два действия: сложение (+) и вычитание (–). Требуется написать программу, которая вычисляет сумму или разность чисел в троично-симметричной системе счисления. Таблица Пифагора для сложения цифр в троично-симметричной системе счисления имеет вид: