--->
164 задач
<---
Источники
#1108
Темы:
[Условный оператор (if)]
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
256 megabytes
Те, кто часто путешествуют самолетами, любят просить место у прохода. Ведь если сидеть у прохода, можно встать и прогуляться, не тревожа своих соседей.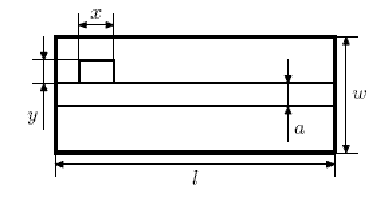
Компания «Аэротрам» готовит к производству новый самолет «T-239-n». Перед инженерами встала задача спланировать организацию салона, чтобы как можно больше мест было у прохода. Будем использовать следующую упрощенную математическую модель салона самолета. В горизонтальном сечении салон представляет собой прямоугольник длиной l и шириной w сантиметров. Кресло представляет собой прямоугольник размером x на y сантиметров и должно быть расположено в салоне так, чтобы его сторона длиной x была параллельна стороне салона длиной l. Проход представляет собой полосу шириной a, параллельную стороне салона длиной l. Проход идет вдоль всего салона.
В салоне требуется разместить n кресел. Помогите инженерам компании выяснить, как организовать салон, чтобы максимальное количество кресел было расположено у прохода. В салоне необходимо сделать хотя бы один проход. Кресло считается расположенным у прохода, если оно имеет хотя бы одну общую сторону с проходом.
Входные данные
Входной файл содержит шесть целых чисел: n, l, w, x, y и a (1 ≤ n ≤ 10000, 1 ≤ l,w,x,y,a ≤ 104).
Выходные данные
Если разместить n кресел в салоне так, чтобы был хотя бы один проход, невозможно, выведите в выходной файл единственное число −1 . Иначе выведите максимальное количество кресел, которое можно разместить у прохода.
Комментарий к примерам тестов.
В первом примере оптимально расположить кресла, например, следующим образом:
Примеры
Входные данные
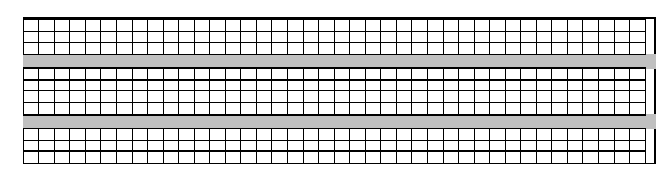
400 3250 750 80 60 70
Выходные данные
160
Входные данные
450 3250 750 80 60 70
Выходные данные
-1
#1178
Темы:
[Целые числа]
[Условный оператор (if)]
Источники:
[
Личные олимпиады,
Всероссийская олимпиада школьников,
Муниципальный этап,
Москва,
2008,
Задача A
]
Витя подключен к интернет по следующему тарифному плану. Ежемесячная абонентская плата составляет A рублей, и в эту абонентскую плату включено B мегабайт трафика. Неизрасходованные мегабайты в конце месяца «сгорают». Если трафик превышает B мегабайт, то каждый мегабайт трафика сверх предоплаченных стоит C рублей.
Известно, что за прошлый месяц Витя израсходовал D мегабайт трафика. Определите, во сколько обошелся ему доступ в интернет в прошлом месяце (считая в том числе и абонентскую плату)?
Входные данные
Вводятся четыре натуральных числа A, B, C, D. Все числа не превышают 100.
Выходные данные
Выведите одно число — сумму (в рублях), которую Витя должен заплатить за интернет.
Примеры
Входные данные
100 10 12 15
Выходные данные
160
Входные данные
100 10 12 1
Выходные данные
100
#1180
Темы:
[Условный оператор (if)]
Источники:
[
Личные олимпиады,
Всероссийская олимпиада школьников,
Муниципальный этап,
Москва,
2008,
Задача C
]
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes
В новой программе OpenCalculator появилась новая возможность – можно настроить, какие кнопки отображаются, а какие – нет. Если кнопка не отображается на экране, то ввести соответствующую цифру с клавиатуры или копированием из другой программы нельзя. Петя настроил калькулятор так, что он отображает только кнопки с цифрами x, y, z. Напишите программу, определяющую, сможет ли Петя ввести число N, а если нет, то какое минимальное количество кнопок надо дополнительно отобразить на экране для его ввода.
Входные данные
Сначала вводятся три различных числа из диапазона от 0 до 9: x, y и z (числа разделяются пробелами). Далее вводится целое неотрицательное число N, которое Петя хочет ввести в калькулятор. Число N не превышает 10000.
Выходные данные
Выведите, какое минимальное количество кнопок должно быть добавлено для того, чтобы можно было ввести число N (если число может быть введено с помощью уже имеющихся кнопок, выведите 0)
1. Число может быть введено имеющимися кнопками.
2. Нужно добавить кнопку 0.
3. Нужно добавить кнопки 1 и 2.
Примеры
Входные данные
1 2 3 1123
Выходные данные
0
Входные данные
1 2 3 1001
Выходные данные
1
Входные данные
5 7 3 123
Выходные данные
2
#1183
Темы:
[Условный оператор (if)]
Источники:
[
Командные олимпиады,
Московская командная олимпиада,
9-11 классы,
2007,
Лига А,
Задача A
]
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes
Напишите программу, которая по изображению поля для игры в «Крестики-нолики» определит, могла ли такая ситуация возникнуть в результате игры с соблюдением всех правил.
Напомним, что игра в «Крестики-нолики» ведется на поле 33. Два игрока ходят по очереди. Первый ставит крестик, а второй – нолик. Ставить крестик и нолик разрешается в любую еще не занятую клетку поля. Когда один из игроков поставит три своих знака в одной горизонтали, вертикали или диагонали, или когда все клетки поля окажутся заняты, игра заканчивается.
Входные данные
Вводится три строки по три числа в каждой, описывающих игровое поле. Число 0 обозначает пустую клетку, 1 – крестик, 2 – нолик. Числа в строке разделяются пробелами.
Выходные данные
Требуется вывести слово YES, если указанная ситуация могла возникнуть в ходе игры, и NO в противном случае.
Примеры
Входные данные
1 1 1 1 1 1 1 1 1
Выходные данные
NO
Входные данные
2 1 1 1 1 2 2 2 1
Выходные данные
YES
Входные данные
1 1 1 2 0 2 0 0 0
Выходные данные
YES
Входные данные
0 0 0 0 1 0 0 0 0
Выходные данные
YES
Входные данные
1 1 1 2 2 2 0 0 0
Выходные данные
NO
#1221
Темы:
[Условный оператор (if)]
Источники:
[
Личные олимпиады,
Всероссийская олимпиада школьников,
Региональный этап,
Московская областная олимпиада,
2007,
Задача A
]
На поле, состоящем из M*N белых квадратных клеток единичного размера, некоторые клетки покрасили в чёрный цвет, в результате чего образовалось одна или несколько закрашенных фигур. Фигура называется связной, если из любой ее клетки можно
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
добраться до любой другой, ходя только по клеткам фигуры и перемещаясь каждый раз в одну из 4‑х соседних по стороне клеток. Несвязные фигуры считаются различными. Например, на данном рисунке приведены 3 фигуры. Периметр фигуры — это сумма длин ее внешних и внутренних (при наличии) сторон. Периметр фигур, изображенных на рисунке: 28, 6 и 4. Суммарный периметр фигур равен 38.
Требуется написать программу, которая находит суммарный периметр фигур, получившихся на клетчатом поле.
Входные данные
Первая строка входных данных содержит два целых числа M и N
(0 < M , N ≤ 100) — количество строк и столбцов, из которых состоит клетчатое поле. Во второй строке находится одно число K (0 ≤ K ≤ M*N) – количество клеток, закрашенных в черный цвет.
В последующих K строках содержатся координаты закрашенных клеток в формате:
<номер строки><пробел><номер столбца>.
Выходные данные
Выведите одно число — суммарный периметр всех фигур.
Примеры
Входные данные
5 5 13 1 1 1 2 1 3 2 2 2 4 3 2 3 3 3 4 4 2 4 4 5 3 5 4 5 5
Выходные данные
28
Выбрано
:
|