На плоскости задан квадрат координатами двух своих противоположных вершин. Найти координаты остальных двух вершин квадрата. Результат вывести с точностью до 0,01.
В первой строке вводятся x1 и y1 — координаты одной из вершин квадрата через пробел, во второй строке вводятся x2 и y2 — координаты противоположной вершины квадрата через пробел. Все числа по модулю не превышают 100.
В первой строке вывести с точностью до 0,01 координаты третьей вершины квадрата x3 и y3 через пробел. Во второй строке вывести с точностью до 0,01 координаты четвертой вершины квадрата x4 и y4 через пробел.
7 3 2 4
5.00000 6.00000 4.00000 1.00000
Новый мэр крупного города Флатбурга Иван Котянин начал свою работу с решения проблем с пробками в городе. Как и в любом крупном городе, во Флатбурге есть кольцевая автодорога. Во Флатбурге она представляет собой монотонный многоугольник. Монотонным называется многоугольник, с которым каждая прямая, проходящая строго с севера на юг, имеет не более двух общих точек.
После совещания с правительством города было принято решение построить новую магистраль — скоростной диаметр, который вел бы строго с севера на юг и соединял две точки кольцевой автодороги.
Помимо борьбы с пробками решено было обновить рекорд по протяженности самой длинной магистрали, проложенной с севера на юг. Для того чтобы обновить рекорд необходимо построить магистраль длиной хотя бы \(d\) километров, а поскольку лишних денег в бюджете Флатбурга не так уж и много, решено было построить дорогу длиной ровно \(d\).
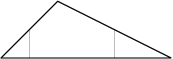
Министр транспорта Флатбурга решил предоставить мэру все варианты строительства новой дороги. Для начала он решил подсчитать, сколько существует способов построить магистраль. Помогите министру.
Первая строка входного файла содержит два целых числа \(n\) — количество вершин у многоугольника, задающего кольцевую автодорогу (\(3 \le n \le 100000\)), и \(d\) — длину новой магистрали (\(1 \le d \le 10^8\)).
Далее следует описание расположения вершин — каждая из следующих \(n\) строк содержит координаты \(x\) и \(y\) (\(-10^8 \le x, y \le 10^8\)) соответствующей вершины. Вершины заданы в порядке их обхода против часовой стрелки.
Направлению с севера на юг соответствуют прямые, задаваемые уравнением \(x = c\) для некоторого \(c\). Заданный многоугольник является монотонным.
В выходной файл выведите количество способов построить дополнительную
магистраль длиной ровно \(d\). Если способов постройки бесконечно много,
выведите в выходной файл «Infinity».
Напишите функцию, вычисляющую длину отрезка по координатам его концов. С помощью этой функции напишите программу, вычисляющую периметр треугольника по координатам трех его вершин.
На вход программе подается \(6\) целых чисел — координат \(x_1,\, y_1,\, x_2,\, y_2,\, x_3,\, y_3\) вершин треугольника. Все числа по модулю не превосходят \(30\,000\).
Выведите значение периметра этого треугольника с точностью до \(6\) знаков после десятичной точки.
0 0 1 0 0 1
3.4142135624
Дан угол AOB (O - вершина угла, A и B - точки на сторонах) и точка P. Определите, принадлежит ли точка P углу AOB (включая его стороны: лучи OA и OB).
Программа получает на вход координаты точек A, O, B, P. Все координаты - целые, не превосходят 100 по модулю. Точки A, O, B не лежат на одной прямой.
Программа должна вывести слово YES или NO.
0 1 0 0 1 0 1 1
YES
Даны два луча: AB и CD (A и C - вершины лучей, B и D лежат на лучах). Проверьте, пересекаются ли они.
Программа получает на вход координаты точек A, B, C, D. Все координаты - целые, не превосходят 100 по модулю.
Программа должна вывести слово YES или NO.
0 1 1 2 1 -1 1 0
YES