В городе, являющемся одним из ведущих Российских образовательных центров, решили построить пивную. Естественно, что ректоры находящихся в городе ВУЗов потребовали, чтобы пивная была максимально удалена от каждого из ВУЗов. Помогите директору будущей пивной выбрать оптимальное место для строительства. Граница города представляет собой выпуклый многоугольник. Положение ВУЗов задается координатами точек внутри этого многоугольника. Пивную нужно построить так, чтобы расстояние от нее до ближайшего вуза было максимально. Пивную можно строить как внутри города, так и на его границе.
В первой строке потока ввода задается число \(3 \le N \le 10\) – количество вершин многоугольника, являющегося границей города. В следующей строке – \(2*N\) вещественных чисел по модулю не превосходящих 1000, являющихся координатами вершин многоугольника, перечисленными в порядке обхода границы города против часовой стрелки. Никакие две вершины многоугольника не совпадают, никакие три не лежат на одной прямой. В третьей строке потока ввода находится число \(1 \le M \le 100\) – количество ВУЗов в городе. В следующей строке – \(2 * M\) вещественных чисел по модулю не превосходящих 1000, являющихся координатами каждого из ВУЗов(никакие два ВУЗа не расположены в одной точке).
В первую строку выходного потока вывести минимальное расстояние от планируемого места строительства пивной до ближайшего к ней ВУЗа. Во второй строке вывести через пробел координаты места, оптимального для строительства пивной. Результаты выводить с двумя цифрами после точки.
Все вещественные числа задаются не более чем с двумя значащими цифрами после точки.
3 0 0 4 1 0 3 1 1 1
3.00 4.00 1.00
Флатландский валун имеет форму многоугольника (не обязатеьно выпуклого). Для простоты будем рассматривать только многоугольники, у которых любые 3 вершины не лежат на одной прямой. Такие валуны получаются из разных видов камней, необязательно однородной плотности. Тем не менее, вы знаете расположение его центра тяжести.
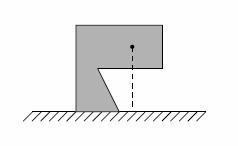Сейчас мы положили на горизонтальную прямую две вершины камня (назовём их базовыми), и отпустили. В случае, если центр тяжести находится над отрезком, соединяющим базовые вершины, или над базовыми вершинами, то валун будет стоять. Иначе сила тяжести заставит его катится в определённом направлении.
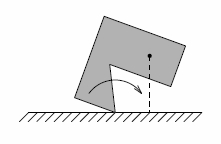
Валун будет перемещаться на одной из базовых вершин, пока он не коснётся горизонтальной прямой другой вершиной. Будем называть этот процесс поворотом. Теперь одна из базовых вершин поменялась, и возможно центр тяжести теперь находится над отрезком, соединяющим базовые вершины. В этом случае валун остановится.
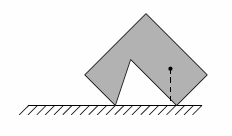
Иначе он продолжит вращаться, пока в конце концов не остановится, так как во Флатляндии вечный двигатель невозможен. Движение валуна происходит в вязкой среде, то есть инерция отсутствует, и валун остановится, как только сила тяжести позволит ему. Зная координаты вершин валуна и его центра тяжести, вычислите количество поворотов, которые совершит валун перед остановкой.
Входной файл содержит целое число N (3 ≤ N ≤ 100) . В следующих N + 1 строках находятся пары целых чисел. Первые N пар описывают координаты вершин валуна, перечисленные в порядке обхода по или против часовой стрелки (линия, на которой стоит валун, описывается уравнением y = 0 ; гравитация действует параллельно Oy в стороны отрицательных y ). Последняя пара чисел описывает центр тяжести. Все координаты — целые числа, не превосходящие по абсолютному значению 30 000 , все y -координаты — неотрицательные. Никакие 3 вершины не лежат на одной прямой. Центр тяжести находится внутри валуна.
Выведите одно число — количество поворотов
Рассмотрим 3D модель системы координат OXYZ . Ось OX направлена направо, ось OY наверх, ось OZ от нас. В пространстве находятся прямоугольные окна. Плоскость каждого окна параллельна плоскости OXY , т.е. его стороны параллельны осям OX и OY . Все окна находятся на разной глубине (различные координаты z > 0).
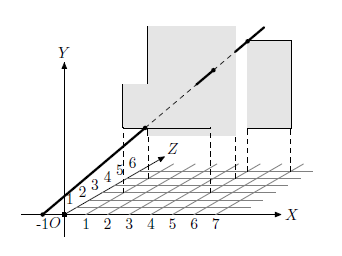
Гангстер с ружьем двигается вдоль оси OX ( y = 0, z = 0 ). Он может выстрелить пулей по прямой линии. Его цель одним выстрелом пробить все окна. Просто касания окна по ребру достаточно, чтобы оно разбилось. Ваша задача определить как совершить такой выстрел.
Первая строка содержит одно число n ( 2 ≤ n ≤ 100 ) - число окон в пространстве. Следующие n строк описывают окна. Каждая строка содержит 5 целых чисел x 1 i , y 1 i , x 2 i , y 2 i , z i ( 1 ≤ x 1 i , y 1 i , x 2 i , y 2 i , z i ≤ 1000 ). Здесь ( x 1 i , y 1 i , z i ) - координаты нижнего левого угла, а ( x 2 i , y 2 i , z i ) - координаты верхнего правого угла. Все окна имеют ненулевую площадь. Окна отсортированы по координате z .
Выведите единственное слово "UNSOLVABLE", если гангстер не может достичь своей цели.
Иначе выведите слово "SOLUTION". На следующей строке выведите x координату точки из которой должен выстрелить гангстер. В следующих n строках выведите x , y , z - координаты точек в которых пуля пробьет i -ое окно. Все координаты должны быть выведены с точностью 6 знаков после запятой.
3 1 3 5 5 3 1 2 5 7 5 5 2 7 6 6
SOLUTION -5.0000000000 1.0000000000 3.0000000000 3.0000000000 5.0000000000 5.0000000000 5.0000000000 7.0000000000 6.0000000000 6.0000000000
3 2 1 5 4 1 3 5 6 8 2 4 3 8 6 4
UNSOLVABLE
В одном очень большом городе устраивают необычные скачки. От обычных скачек они отличаются тем, что проходят не на ипподроме, а на специально заготовленной трассе. Она представляет из себя бесконечную прямую на плоскости.
Трасса очень длинная, поэтому соревнования могут затягиваться не на один день и проходить не только днем, но и ночью. Организаторы глубоко задумались о том, как они будут освещать трассу, ведь освещать бесконечно длинную трассу не так уж и просто. Для этого они закупили N прожекторов, которые будут установлены в некоторых точках города. Известно что прожекторы освещают землю, образуя круги.
Так получилось, что компания, которая устанавливала оборудование, перепутала места установки, поэтому некоторые прожекторы могут вообще не освещать трассу. Теперь соревнование может потерпеть неудачу, организаторы очень обеспокоены тем, что зрители не увидят самые интересные моменты соревнований из-за ошибки мастеров. Помогите организаторам выяснить, какова длина освещенной части трассы.
Первая строка входного файла содержит четыре числа x 1 , y 1 , x 2 , y 2 — координаты двух точек на прямой. Во второй — строке число N ( 1 ≤ N ≤ 100000 ) — количество прожекторов. В каждой их следующих N строк заданы 3 числа x , y и R , координаты и радиус кругов, образованных прожекторами.
Все координаты и радиусы — целые числа, не превышающие по модулю 10 5 .
В выходной файл выведите ответ на задачу, с точностью до 10 - 4 .
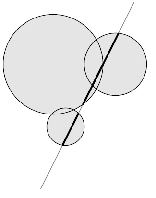
0 0 1 1 1 5 5 1
2.000000000000001
1 1 2 3 3 5 5 5 -5 5 8 -3 -5 3
18.446020156281286
Завтра состоится футбольный матч между двумя знаменитыми командами: Газмясом и Нефтьрыбом. Матч будет проходить на поле длины L и ширины W . Матч будет судить профессиональный футбольный судья в четвертом поколении Вениамин Хлебников.
Быть судьей — ответственное и не всегда безопасное занятие. Поэтому Вениамин решил проработать некоторые игровые эпизоды, которые возникнут в завтрашней игре.
Рассмотрим ситуацию, когда игрок A делает пас игроку B — то есть, передает ему мяч по отрезку, соединяющему точки, в которых находятся игроки. С одной стороны, судья должен хорошо видеть то, что происходит во время паса; с другой стороны, согласно требованиям безопасности, судья не может находиться слишком близко к мячу. Поэтому во время паса судья должен находиться на расстоянии, не меньшем, чем r , и не большем, чем R , от возможного положения мяча. При этом считается, что все то время, в течение которого движется мяч, судья стоит на одном месте. Разумеется, судья должен все время матча находиться на поле.
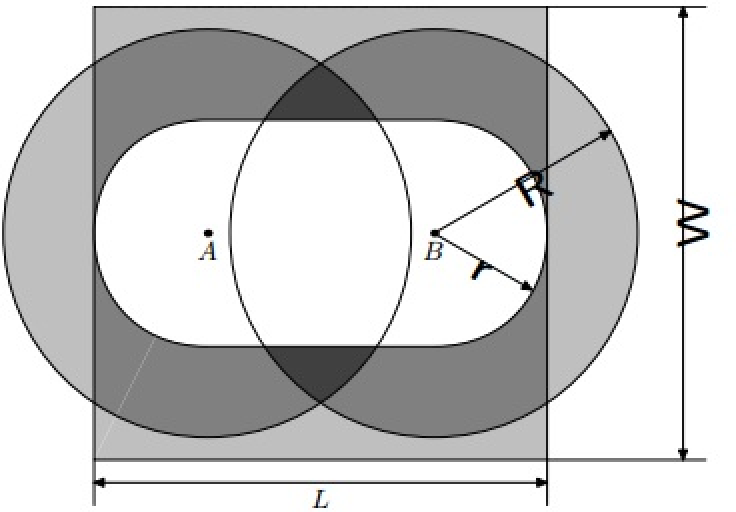
Так как эти условия достаточно сложны, то даже опытному судье иногда бывает трудно определить, где он должен находиться в момент паса. По этой причине Вениамин хочет перед матчем потренироваться находить те области, где он может находиться, при различных начальных условиях. Для того чтобы сравнить свой ответ с правильным, ему необходима программа, которая по заданным размерам поля, координатам игроков и числам r и R находит площадь тех областей поля, в которых может находиться судья. Помогите ему!
В первой строке входного файла даны два целых положительных числа L и W ( 1 ≤ L , W ≤ 100 ) — длина и ширина поля.
Во второй строке даны целые числа X A , Y A , X B , Y B — координаты игроков A и B соответственно. Так как игроки находятся на поле, то 0 ≤ X A , X B ≤ L , 0 ≤ Y A , Y B ≤ W .
В третьей строке даны целые числа
r
и
R
(
0 <
r
<
R
< 100
). Известно, что
R
≤
D
, где
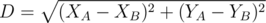— расстояние между игроками
A
и
B
.
В выходной файл выведите ответ на задачу. Ответ принимается, если он отличается от корректного не более, чем на 10 - 6 .
20 20 5 10 15 10 5 9
13.956675119742911