Вы наверняка слышали легенду о Короле Артуре и Рыцарях Круглого Стола. Практически все версии этой истории указывают на то, что круглость Круглого Стола тесно связана с верой Артура в равенство среди рыцарей. Это ложь! На самом деле выбор Артура касательно формы стола вызван его детской травмой.
В реальности Артур был принужден убирать и мыть квадратные столы с юного возраста после того как на них играли в бирюльки. После соревнований по этой игре обычно на столе остается множество палочек, не касающихся друг друга. В духе соревнования, организаторы установили свод строгих правил для уборщиков. Точнее, палочки со стола должны быть убраны одна за другой путем их сдвига к ближайшему к уборщику краю стола. Они не должны вращаться и касаться других палочек в процессе перемещения.
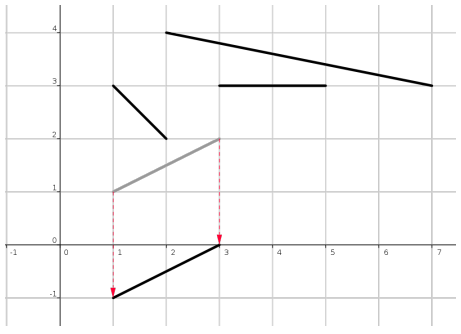
В этой задаче представим стол на координатной плоскости как квадрат с противоположными вершинами в точках (0, 0) и (10000, 10000), где палочкам соответствуют прямые отрезки, лежащие внутри квадрата. Предположим, что Артур сидит у края стола, прилежащего к оси X. Тогда уборка палочек со стола сводится к передвижению их к оси X, покуда они не упадут со стола. Ваша задача - определить порядок уборки палочек со стола, который соответствует условиям из предыдущего абзаца.
Первая строка содержит единственное целое число N ( 1 ≤ N ≤ 5000 ) - количество палочек на столе. Каждая из следующих N строк содержит 4 целых числа x 1 , y 1 , x 2 , y 2 ( 0 ≤ x 1 , y 1 , x 2 , y 2 ≤ 10000 ), обозначающих крайние точки палочек.
В единственной строке выведите N целых чисел - номера палочек в том порядке, в котором они должны быть убраны со стола. Если существует несколько решений, выведите любое из них.
4 1 3 2 2 1 1 3 2 2 4 7 3 3 3 5 3
2 4 1 3
4 0 0 1 1 1 2 0 3 2 2 3 3 4 0 3 1
4 3 1 2
3 4 6 5 5 2 1 15 1 3 2 8 7
2 3 1
Дима архитектор. А ещё Дима фотограф. Он часто носится по свету и фотографирует местные Биг Бены и прочие крутые сооружения.
На этот раз Дима приехал в Берляндию, знаменитую своим метрополитеном. Он состоит из n линий, каждая из которых представлена прямой на карте города. На пересечении каждых двух линий метрополитена расположены станции, наземные павильоны которых признаны национальными памятниками архитектуры. Как только Дима увидел их с экрана своего смартфона, он мгновенно загорелся желанием их сфотографировать.
Специально для этой цели он решил воспользоваться маршрутным вертолётом, с которого планирует осуществлять съёмку. Вертолёты компании летают по t маршрутам. Каждый маршрут представляет собой прямую линию. Дима может сделать фотографию, находясь в любой точке маршрута, однако, чем меньше расстояние до станции, тем больше деталей будет видно на снимке, и он соберёт больше лайков в социальных сетях. Вот тут Диме нужна ваша помощь.
Вам даны n прямых, задающих линии метро, и t прямых, задающих доступные вертолётные маршруты. Дима просит для каждого маршрута найти расстояние до ближайшей к нему станции.
Гарантируется, что никакие две линии метрополитена не совпадают и что любые две линии пересекаются, а также, что любые два маршрута пересекаются и что любой маршрут пересекается с любой линией.
В первой строке входного файла находятся два числа n и t ( 2 ≤ n ≤ 100 000 , 1 ≤ t ≤ 20 ) — количество линий метро и количество возможных маршрутов, соответственно.
В следующих n строках содержатся по три целых числа a i , b i и c i ( | a i |, | b i | ≤ 10 000 , a i 2 + b i 2 > 0 , | c i | ≤ 10 8 ), описывающие линии метро. Каждая линия представляет собой прямую a i · x + b i · y + c i = 0 .
Затем следуют t строк с описанием возможных вертолётных маршрутов, каждая из них содержит три целых числа u i , v i , w i ( | u i |, | v i | ≤ 10 000 , u i 2 + v i 2 > 0 , | w i | ≤ 10 8 ). Аналогично, каждый маршрут представляет собой прямую u i · x + v i · y + w i = 0 .
Для каждого маршрута выведите единственное вещественное число — расстояние между
i
-м вертолётным маршрутом и наиболее близкой к нему станцией. Ваш ответ будет считаться правильным, если его абсолютная или относительная погрешность относительно ответа жюри не будет превосходить
10
- 9
, то есть,
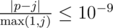, где
p
— ответ участника, а
j
— ответ жюри.
Тесты по данной задаче состоят из пяти групп. Баллы за каждую группу ставятся только при прохождении всех тестов группы и всех тестов предыдущих групп кроме, возможно, тестов из условия.
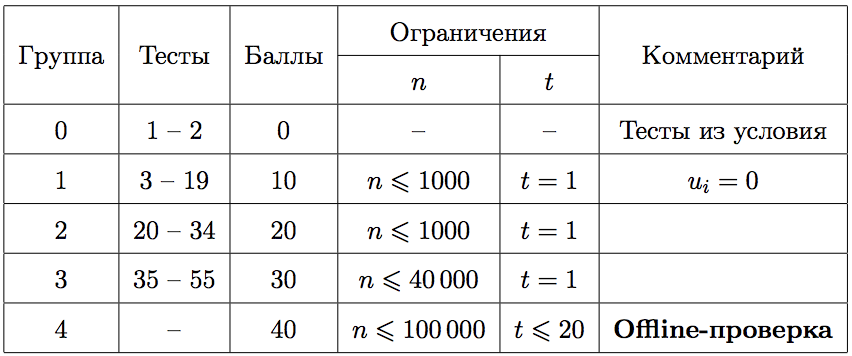
Изображения к тестами из условия приведены ниже.
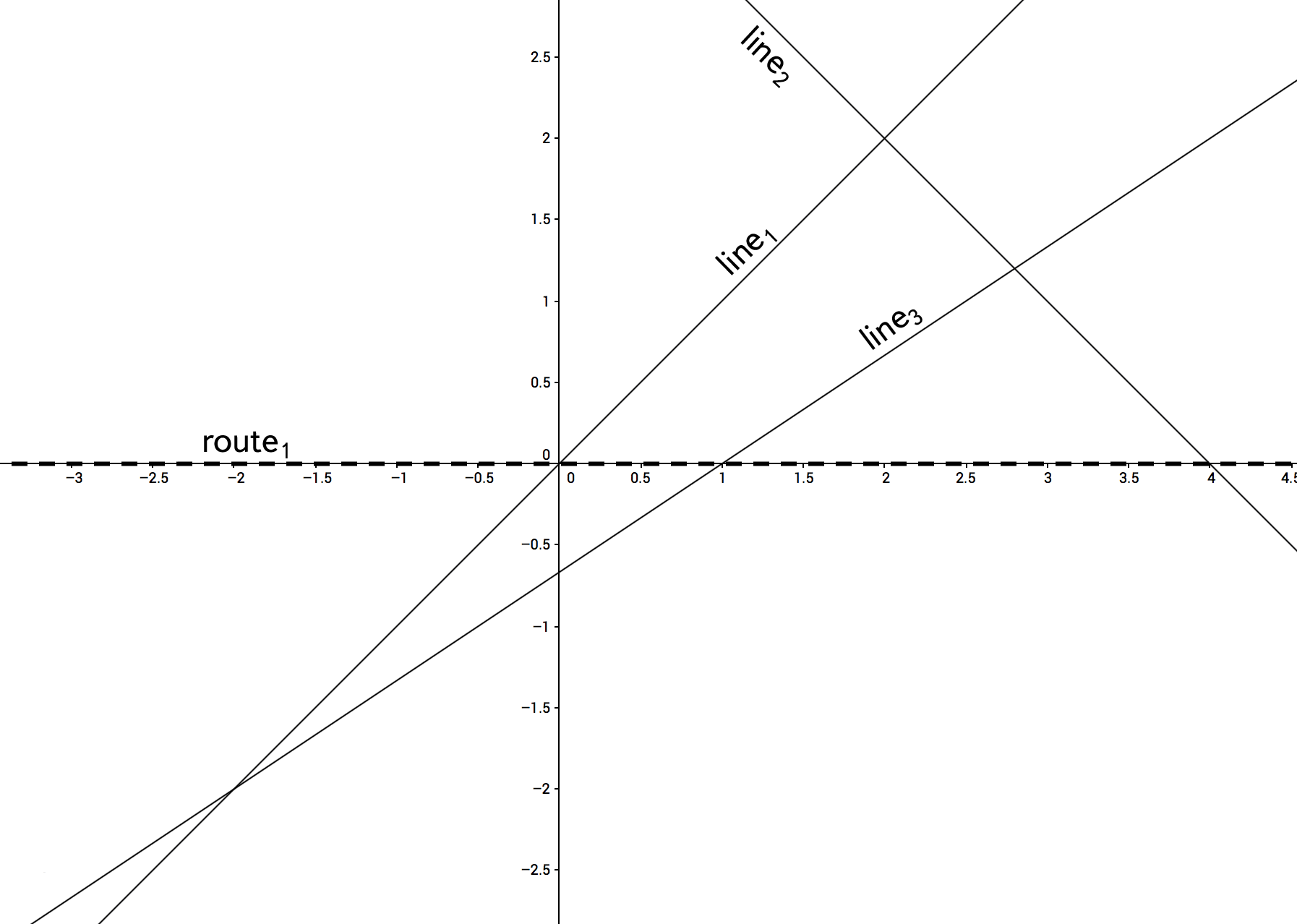
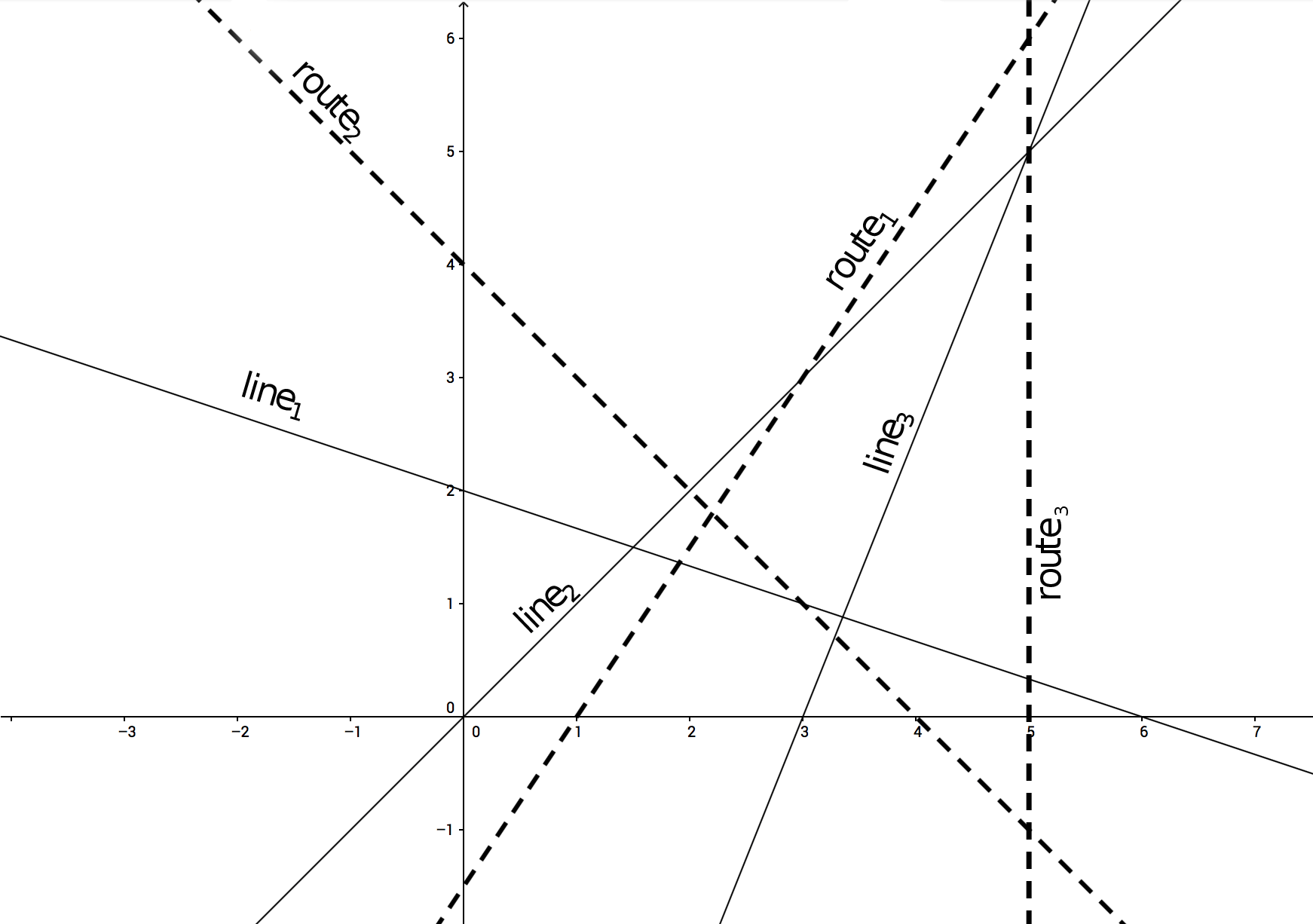
3 1 1 -1 0 1 1 -4 4 -6 -4 0 1 0
1.20000000000000000000
3 3 1 3 -6 -1 1 0 -5 2 15 3 -2 -3 -1 -1 4 1 0 -5
0.41602514716892186000 0.16637806616154061000 0.00000000000000000000
Хранители в опасности, и Доктор Манхэттен со своим другом Дэниелом Драйбергом должны срочно их предупредить. Всего в команде хранителей n человек, i -й из которых находится в точке плоскости с координатами ( x i , y i ) .
Как всем известно, доктор Манхэттен вычисляет расстояние между двумя хранителями
i
и
j
по формуле
|
x
i
-
x
j
| + |
y
i
-
y
j
|
. Дэниел, как обычный человек, считает, что расстояние равно
.
Сейчас успех операции зависит от того, сколько существует пар ( i , j ) ( 1 ≤ i < j ≤ n ), таких что расстояние между хранителем i и хранителем j , вычисленное Доктором Манхэттеном, равняется расстоянию между ними, вычисленному Дэниелом. Вычислить эту величину попросили именно вас.
В первой строке входных данных записано число n ( 1 ≤ n ≤ 200 000 ) — количество хранителей.
В каждой из следующих n строк записаны два целых числа x i и y i ( | x i |, | y i | ≤ 10 9 ).
Выведите количество пар хранителей, таких что расстояние между ними, вычисленное доктором Манхэттеном, равно расстоянию, вычисленному Дэниелом.
Тесты к этой задаче состоят из трёх групп. Баллы за каждую группу ставятся только при прохождении всех тестов группы и всех тестов предыдущих групп.
В первом примере расстояние между хранителем
1
и хранителем
2
равняется
|1 - 7| + |1 - 5| = 10
в понимании Доктора Манхэттена и
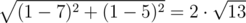в понимании Дэниела. Для пар
(1, 1)
,
(1, 5)
и
(7, 5)
,
(1, 5)
расстояния, вычисленные Доктором Манхэттеном и Дэниелом, совпадают.
3 1 1 7 5 1 5
2
6 0 0 0 1 0 2 -1 1 0 1 1 1
11
Вы знаете, в чём разница между отелем и мотелем? Верно, разница в количестве мух, которые там живут. Норман – владелец одного из самых популярных мотелей в Америке,но его мать хочет, чтобы он стал отелем. Именно поэтому Норман купил мухобойку ( мухобойка – инструмент для отпугивания или прихлопывания мух. Может представлять собой как пластиковое или резиновое изделие на длинной ручке, так и пучок волос или листьев). Мухобойка представляет из себя многоугольник из \(\)\(K\)\(\) рёбер.
Желая угодить своей матери, Норман встал у окна, на котором сидели \(\)\(N\)\(\) мух. Так как норманн – пацифист, он не может причинить вред другому живому существу, в том числе, мухе. Именно поэтому ему интересно количество способов ударить по окну мухобойкой, не задев ни одной мухи.
Окно представляет из собой прямоугольник с левой нижней вершиной в точке \(\)\((0, 0)\)\(\) и правой верхней – в точке \(\)\((X_p, Y_p)\)\(\). После того как Норман ударит по окну все вершины многоугольника должны лежать в точках с целыми координатами, а мухобойка должна полностью лежать внутри прямоугольника окна. Норману интересно, сколькими способами он может ударить по окну, не убив ни единой мухи.
Первая строка содержит три числа \(\)\(X_p, Y_p, N\)\(\) (\(\)\(1 \leq X_p, Y_p \leq 500\)\(\), \(\)\(0 \leq N \leq X_p\cdot Y_p\)\(\)) — координаты верхней правой точки окна и количество мух на окне соответственно.
Следующие \(\)\(N\)\(\) строк содержат по \(\)\(2\)\(\) целых числа \(\)\(x_i, y_i\)\(\), задавая координаты мух на окне (\(\)\(0 < x < X_p\)\(\), \(\)\(0 < y_i < Y_p\)\(\)).
В следующей строке вводится одно число \(\)\(K\)\(\) (\(\)\(3 \leq K \leq 10\,000\)\(\)) — количество вершин многоугольника мухобойки. Следующие \(\)\(K\)\(\) строк содержат по два числа \(\)\(x_j, y_j\)\(\) (\(\)\(-10^9 \leq x_j, y_j \leq 10^9\)\(\)), задавая \(\)\(j\)\(\)-ю вершину многоугольника. Вершины многоугольника заданы в порядке обхода по или против часовой стрелке.
Выведите искомое число способов ударить по окну, не задев ни одной мухи.
Решение, правильно работающее на тестах, в которых \(\)\(1 \leq X_p, Y_p \leq 100\)\(\) будет оцениваться в \(\)\(62\)\(\) балла.
Пояснение к третьему примеру:
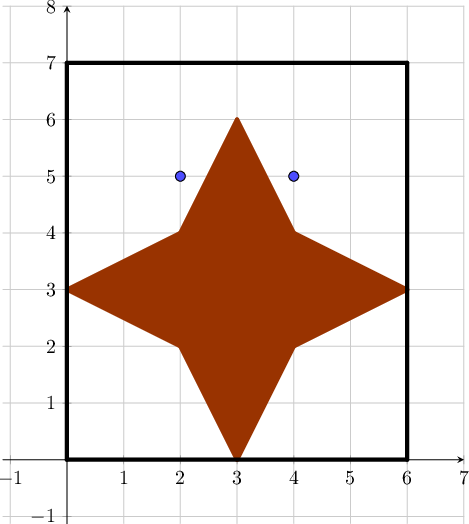
4 5 2 1 3 3 4 4 0 0 2 0 2 2 0 2
4
5 5 3 1 4 1 3 2 2 3 4 7 6 3 7 6
3
6 7 2 2 5 4 5 8 1 4 3 3 4 1 5 3 7 4 5 5 4 7 3 5
1
Организаторы CEOI 2011 собираются устроить вечеринку с кучей воздушных шариков. Всего будет \(n\) шариков (они все имеют форму идеального шара), и они будут лежать на одной линии на полу.
Шарики ещё не надуты, и каждый из них изначально имеет нулевой радиус. Ещё, \(i\)-й шар прикреплён к полу в позиции \(x_i\). Они будут надуваться последовательно, слева направо. Когда какой-то шарик надувается, его радиус непрерывно увеличивается, пока не достигнет верхней границы своего размера, \(r_i\), либо же не каснётся одного из уже надутых.
Картинка 1: Шары из примера, после надувания.
Организваторы хотели бы оценить, сколько воздуха понадобится для надувания. Найдите, пожалуйста, итоговый радиус каждого шара.
В первой строке входных данных содержится целое число \(n\) (\(1\le n\le 200 000\)) – количество шаров.
Следующие \(n\) описывают шары. \(i\)-я из них содержит два целых числа \(x_i\) и \(r_i\) (\(0\le x_i\le 10^9\)), \(1\le r_i\le 10^9\)). Последовательность \(x_i\) строго возрастает.
Выведите \(n\) строк, в \(i\)-й строке должно быть единственное целое число – радиус \(i\)-го шара после надувания. Ваш ответ будет считаться верным, если он отличается от правильного не больше, чем на 0.001 в каждом числе.
1. (40 баллов) \(n\le 2000\).
2. (60 баллов) \(n\le 200000\).
3 0 9 8 1 13 7
9.000 1.000 4.694