--->
118 задач
<---
Источники
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes
Мальчику Васе очень нравится известная игра "Сапер" ("Minesweeper").
В "Сапер" играет один человек. Игра идет на клетчатом поле (далее будем называть его картой) NxM (N строк, M столбцов). В K клетках поля стоят мины, в остальных клетках записано либо число от 1 до 8 - количество мин в соседних клетках, либо ничего не написано, если в соседних клетках мин нет. Клетки являются соседними, если они имеют хотя бы одну общую точку, в одной клетке не может стоять более одной мины. Изначально все клетки поля закрыты. Игрок за один ход может открыть какую-нибудь клетку. Если в открытой им клетке оказывается мина - он проигрывает, иначе игроку показывается число, которое стоит в этой клетке, и игра продолжается. Цель игры — открыть все клетки, в которых нет мин.
У Васи на компьютере есть эта игра, но ему кажется, что все карты, которые в ней есть, некрасивые и неинтересные. Поэтому он решил нарисовать свои. Однако фантазия у него богатая, а времени мало, и он хочет успеть нарисовать как можно больше карт. Поэтому он просто выбирает N, M и K и расставляет мины на поле, после чего все остальные клетки могут быть однозначно определены. Однако на определение остальных клеток он не хочет тратить свое драгоценное время. Помогите ему!
По заданным N, M, K и координатам мин восстановите полную карту.
Входные данные
В первой строке входного файла содержатся числа N, M и K (1 ≤ N, M, K ≤ 10). Далее идут K строк, в каждой из которых содержится по два числа, задающих координаты мин. Первое число в каждой строке задает номер строки клетки, где находится мина, второе число - номер столбца. Левая верхняя клетка поля имеет координаты (1,1), правая нижняя - координаты (N, M).
Выходные данные
Выходной файл должен содержать N строк по M символов, разделенных пробелами - соответствующие строки карты. j-й символ i-й строки должен содержать символ ‘*‘ (звездочка) если в клетке (i, j) стоит мина, цифру от 1 до 8, если в этой клетке стоит соответствующее число, либо ‘.‘ (точка), если клетка (i, j) пустая и у нее нет мин-соседей.
Примеры
Входные данные
4 4 2 2 2 2 3
Выходные данные
1 2 2 1 1 * * 1 1 2 2 1 . . . .
#3711
ограничение по времени на тест
6.0 second;
ограничение по памяти на тест
256 megabytes
В прямоугольной таблице клетки раскрашены в белый и черный цвета. Найти в ней прямоугольную область белого цвета, состоящую из наибольшего количества ячеек.
Входные данные
Во входном файле записана сначала высота \((N)\), а затем ширина \((M)\) таблицы \(((1 \le N \le 5000)\), \((1 \le M \le 5000))\), а затем записано \((N)\) строк по \((M )\) чисел в каждой строке, где \(0\) означает, что соответствующая клетка таблицы выкрашена в белый цвет, а \(1\) – что в черный.
Выходные данные
В выходной файл вывести одно число — количество клеток, содержащихся в наибольшем по площади белом прямоугольнике.
Примеры
Входные данные
5 6 1 0 0 0 1 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0
Выходные данные
9
#3890
Темы:
[Двумерные массивы]
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
256 megabytes
Фирма, в которой работает ваш друг, решила установить на конечной остановке своих маршруток
большую абстрактную скульптуру со своим логотипом. Скульптура будет представлять собой
прямоугольную сетку из \(N\) строк и \(M\) столбцов, в некоторых узлах которой будут располагаться разноцветные шары.
Для обеспечения жёсткости конструкции шары, расположенные в узлах, соседних по вертикали,
горизонтали или диагонали, необходимо соединить металлическими стержнями. Более строго, два шара
должны быть соединены стержнем, если разность номеров строк, в которых расположены эти шары, не
превосходит по модулю единицы, и разность номеров столбцов тоже не превосходит по модулю единицы.
Напишите программу, которая по заданному расположению шаров позволит определить, как будет выглядеть скульптура после установки стержней.
Входные данные
В первой строке входного файла находятся два натуральных числа \(N\) и \(M\) — размеры конструкции (\(1\leq
N,M\leq 100\)). Далее следуют \(N\) строк по \(M\) символов в каждой. Каждый символ — это или
“#” (решетка), обозначающий, что в соответствующем узле будет находиться шарик, или “.” (точка),
обозначающий, что соответствующий узел будет пустой.
Выходные данные
Выведите в выходной файл \(2N-1\) строку по \(2M-1\) символов в каждой,
изображающие как сами шары, так и соединяющие их стержни. А именно,
в нечётных позициях нечётных строк выведите символ “#”
или “.”, в зависимости от того, заполнен этот узел шариком или нет,
а в остальных позициях выведите один из символов “ ” (пробел),
“-” (минус), “|” (вертикальная
палочка, ASCII #124),
“/” (дробь, ASCII #47), “\” (обратный слеш, ASCII #92) или “X”
(латинская заглавная буква X, ASCII #88), отражающий конфигурацию стержней в соответствующем месте структуры.
Если какая-то строка выходного файла должна заканчиваться на пробелы, их можно не выводить.
Примечание
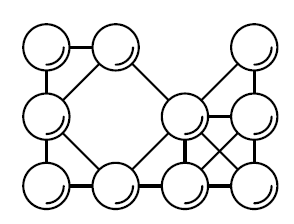
Первый пример соответствует рисунку.
Примеры
Входные данные
3 4 ##.# #.## ####
Выходные данные
#-# . # |/ \ /| # . #-# |\ /|X| #-#-#-#
Входные данные
3 4 .#.. #.#. .#..
Выходные данные
. # . . / \ # . # . \ / . # . .
#3893
Темы:
[Двумерные массивы]
[Задачи на моделирование]
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
256 megabytes
... но нужен ли на самом деле кому-нибудь 6\(1\over7\)-пунктовый шрифт, который на три четверти — шрифт Baskerville, и на четверть — Helvetica?
Дональд Э. Кнут. Идея Мета-фонта1
Маленькая девочка Оля добралась до полки, на которой стоят флаконы с мамиными любимыми духами, и начала заниматься своим любимым занятием — переливанием жидкостей из одного флакона в другой. Когда наконец мама застала её за этим занятием, прекрасная коллекция духов была уже безнадёжно утрачена.
К счастью, Оля — аккуратная девочка, поэтому все свои действия она записывала на бумажку. Помогите ей успокоить маму: определите, каков состав духов в первом (мамином любимом) флаконе, чтобы мама смогла придумать этой смеси новое название и рассказывать всем, какие прекрасные духи она смогла сделать вместе с дочерью.
Считайте, что Оля не пролила ни одной капли, а также что она тщательно встряхивала флаконы после каждого переливания. Учтите, что в маминых флаконах порой не видно, есть ли там жидкость, и потому Оля иногда могла пытаться переливать духи из пустого флакона (в результате, естественно, ничего не переливалось). Вы можете также считать, что после каждого переливания в каждом флаконе каждый тип духов либо полностью отсутствует, либо содержится в объеме не меньшем чем \(10^{-10}\).
Входные данные
На первой строке входного файла находятся два числа \(N\) и \(M\) — количество флаконов и число типов маминых любимых духов соответственно (\(2 \leq N \leq 100\); \(1 \leq M \leq 100\)). Далее следуют \(N\) строк, на \(i\)-ой из которых находятся два числа — тип \(L_i\) и объем \(V_i\) духов, находившихся изначально в \(i\)-ом флаконе (\(1\leq L_i \leq M\); \(0 \leq V_i \leq 1000\)). Возможно, что в нескольких флаконах находились духи одного и того же типа; возможно, что какого-то типа вообще не было на полке.
Далее во входном файле следует строка с числом \(K\) — количеством совершённых переливаний (\(1 \leq K \leq 1000\)). За ней следуют \(K\) строк, на \(k\)-ой из которых находятся три числа \(S_k\), \(T_k\) и \(A_k\) — номера флаконов, откуда и куда переливала Оля при \(k\)-ом переливании, и количество перелитой жидкости (в процентах от количества жидкости в \(S_k\)-ом флаконе перед переливанием). Гарантируется, что \(1\leq S_k,T_k\leq N\), что \(S_k\neq T_k\), и что \(0\leq A_k\leq 100\). Все числа во входном файле целые.
Выходные данные
В выходной файл выведите \(M\) чисел — процентное содержание всех видов духов (от первого до \(M\)-ого) в первом флаконе после последнего переливания. Выводите результат с точностью не меньше двух знаков после запятой. Гарантируется, что после последнего переливания первый флакон оказался непустым.
Примечание
1... but does anybody really need a 6\(1\over7\)-point font that is one fourth of the way between Baskerville and Helvetica? — Donald E. Knuth, The Concept of a Meta-Font
Примеры
Входные данные
3 2 1 100 2 200 1 500 2 3 2 20 2 1 50
Выходные данные
60.00 40.00
ограничение по времени на тест
-1.0 second;
ограничение по памяти на тест
64 megabytes
В этой задаче нужно придумать генератор — однострочное выражение на языке Python, результатом вычисления которого будет двумерный массив (список вложенных списков), заполненный по некоторому правилу.
Например, пусть нужно задать следующий массив (для удобства добавлены дополнительные пробелы между элементами):
0 0 0 0 0 0 0 1 2 3 4 5 0 2 4 6 8 10 0 3 6 9 12 15 0 4 8 12 16 20В этом массиве n = 5 строк, m = 6 столбцов, и элемент в строке i и столбце j вычисляется по формуле: A[i][j] = i * j.
Ответом на это задание будет следующее выражение-генератор:
[[ i * j for j in range(m)] for i in range(n)] Вам нужно создать текстовый файл, записать в его первой строчке заданное выражение (только одно выражение в квадратных скобках, например, достаточно просто скопировать текст, записанный выше) и сдать на проверку данный файл. Не нужно писать инструкции вроде A = [...] или print(...)).
В выражении должны использоваться переменные n и m, означающие число строк и столбцов в массиве. Считывать эти переменные с клавиатуры не нужно, они уже будут автоматически определены на момент запуска вашего решения.
Если в задании сказано, что массив — квадратный, то число строк и столбцов в нем равно n, а значение m не определено и использовать его нельзя.
Проверка будет осуществляться при помощи интерпретатора языка Python версии 3, в частности, это означает, что в генераторах нужно использовать функции range, а не xrange.
Заполните массив целыми числами по образцу в виде таблицы умножения.
Пример для \(n = 5, m = 6\)
0 0 0 0 0 0 0 1 2 3 4 5 0 2 4 6 8 10 0 3 6 9 12 15 0 4 8 12 16 20
Выбрано
:
|