--->
55 задач
<---
Источники
#1307
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes
Для транспортирования материалов из цеха А в цех В используется конвейер. Материалы упаковываются в одинаковые контейнеры и размещаются на ленте один за одним в порядке изготовления в цехе А. Каждый контейнер имеет степень срочности обработки в цехе В. Для упорядочивания контейнеров по степени срочности используют накопитель, который находится в конце конвейера перед входом в цех В. Накопитель работает пошагово, на каждом шаге возможны следующие действия:
накопитель перемещает первый контейнер из ленты в цех В;
накопитель перемещает первый контейнер из строки в склад (в складе каждый следующий контейнер помещается на предыдущий);
накопитель перемещает верхний контейнер из склада в цех В.
Напишите программу, которая по последовательности контейнеров определит, можно ли упорядочить их по степени срочности пользуясь описанным накопителем.
Входные данные
Входной файл в первой строке содержит количество тестов N. Далее следует N строк, каждый из которых описывает отдельный тест и содержит целое число K (1 ≤ K ≤ 10000) — количество контейнеров в последовательности и K действительных чисел — степеней срочности контейнеров в порядке их поступления из цеха А (меньшим числам соответствует большая степень срочности).
Выходные данные
Каждая строка выходного файла должна содержать ответ для одного теста. Необходимо вывести 1, если необходимое упорядочивание возможно, или 0 в противном случае.
Примеры
Входные данные
2 2 2.9 2.1 3 5.6 9.0 2.0
Выходные данные
1 0
#1312
Темы:
[Быстрая сортировка]
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes
Дана последовательность, состоящая из 2N натуральных чисел. Известно, что все числа этой последовательности можно разбить на пары таким образом, что сумма чисел во всех парах будет одинаковой. Например, числа последовательности 99, 23, 77, 1 можно разбить на пары 1+99=77+23.
Напишите программу, которая по такой последовательности определяет, можно ли эту последовательность разбить на пары таким образом, чтобы произведение чисел во всех парах было одинаковым.
Входные данные
Файл содержит данные нескольких тестов. Первая строка содержит натуральное число - количество тестов в файле. Первая строка каждого теста содержит число 2N — количество чисел в последовательности. В каждой из последующих 2N строчек содержится целое число от 1 до 109 — элементы последовательности (1≤N≤ 50000)
Выходные данные
Файл должен содержать ответ на каждый из тестов в отдельной строке. Ответом на тест является символ 1, если входную последовательность можно разбить на пары, произведения в которых были бы одинаковыми, и 0 в противном случае.
Примеры
Входные данные
2 4 99 23 77 1 2 1 10101
Выходные данные
0 1
#1338
Темы:
[Быстрая сортировка]
[Сканирующая прямая]
Источники:
[
Личные олимпиады,
Всероссийская олимпиада школьников,
Заключительный этап,
2009,
Задача B
]
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
256 megabytes
Над ареной огромного спортивного комплекса Независимого Главного Университета (НГУ) решили построить перекрытие. Перекрытие будет построено по клеевой технологии и состоять из склеенных друг с другом блоков. Блок представляет собой легкий прямоугольный параллелепипед. Два блока можно склеить, если они соприкасаются перекрывающимися частями боковых граней ненулевой площади.
НГУ представил план комплекса, имеющий вид прямоугольника размером W на L. При этом один из углов прямоугольника находится в начале системы координат, а другой имеет координаты (W, L). Стены комплекса параллельны осям координат.
Подрядчики известили НГУ, что они готовы к определенному сроку изготовить блоки и установить их. Для каждого блока фиксировано место его возможного монтажа, совпадающее по размерам с этим блоком. Места выбраны так, что ребра блоков параллельны осям координат. Места монтажа блоков не пересекаются.
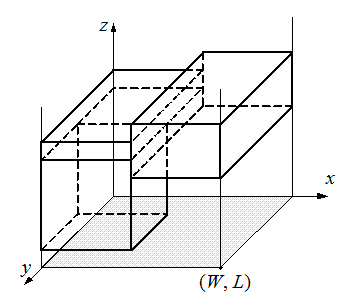
По техническим условиям перекрытие должно состоять из такого набора склеенных блоков, который содержит сплошной горизонтальный слой ненулевой толщины. Торопясь ввести комплекс в эксплуатацию, НГУ решил построить перекрытие из минимально возможного числа блоков.
Требуется написать программу, которая позволяет выбрать минимальное число блоков, которые, будучи установленными на указанных подрядчиками местах, образуют перекрытие, либо определить, что этого сделать невозможно. Высота, на которой образуется перекрытие, не имеет значения.
Входные данные
В первой строке входного файла указаны три целых числа: N — количество возможных блоков (1 ≤ N ≤ 105) и размеры комплекса W и L (1 ≤ W, L ≤ 104). Каждая из последующих N строк описывает место монтажа одного блока, определяемое координатами противоположных углов: (x1, y1, z1) и (x2, y2, z2), при этом 0 ≤ x1 < x2 ≤ W, 0 ≤ y1 < y2 ≤ L, 0 ≤ z1 < z2 ≤ 109. Все числа во входном файле целые и разделяются пробелами или переводами строк.
Гарантируется, что места установки блоков не пересекаются друг с другом.
Выходные данные
Первая строка выходного файла должна содержать либо слово «YES», если перекрытие возможно построить, иначе — слово «NO». В первом случае вторая строка выходного файла должна содержать минимальное число блоков, образующих перекрытие, а последующие строки — номера этих блоков, в соответствии с порядком, в котором они перечислены во входном файле.
Если возможно несколько минимальных наборов блоков, выведите любой из них.
Примечания
Решения, корректно работающие в случае, когда все числа во входном файле не превышают 100, будут оцениваться из 40 баллов.
Примеры
Входные данные
1 10 10 0 0 0 10 10 10
Выходные данные
YES 1 1
Входные данные
2 10 10 0 0 0 10 5 5 0 5 5 10 10 10
Выходные данные
NO
#1341
Источники:
[
Личные олимпиады,
Всероссийская олимпиада школьников,
Заключительный этап,
2009,
Задача E
]
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
256 megabytes
Около прямолинейного забора, состоящего из N одинаковых бетонных плит, проводится конкурс граффити, в котором участвуют M граффити-художников. Художники должны разрисовать все плиты своими произведениями за наименьшее возможное время.
Плиты пронумерованы числами от 1 до N, граффити-художники имеют номера от 1 до M. Первоначально i-й граффити-художник находится около плиты с заданным номером pi. Каждому художнику требуется b минут на разрисовывание любой плиты. Каждую плиту должен разрисовать ровно один граффити-художник.
В начале работы, а также после разрисовывания любой плиты граффити-художник может перейти к любой неразрисованной плите. Время перемещения граффити-художника от любой плиты к соседней с ней одинаково и равно a минут. Таким образом, чтобы перейти от плиты с номером i к плите с номером j художнику требуется a×|i – j| минут.
Требуется написать программу, которая поможет участникам конкурса разрисовать все плиты за минимальное возможное время.
Входные данные
В первой строке входного файла указаны числа N — количество плит в заборе и M — количество граффити-художников (1 ≤ N, M ≤ 100000). Во второй строке заданы два целых числа: a — количество минут, которое требуется для перехода от любой плиты к соседней, и b — количество минут, которое требуется граффити-художнику на разрисовывание одной плиты (1 ≤ a, b ≤ 106). В третьей строке заданы M чисел p1, p2, …, pM — начальные положения граффити-художников (1 ≤ pi ≤ N).
Выходные данные
В первую строку выходного файла выведите минимальное количество минут, требуемых художникам для выполнения работы.
В последующих M строках выведите описание действий художников. В i-й из этих строк должно содержаться описание действий i-го художника: количество плит, которые должен разрисовать этот художник, и номера этих плит в очередности их разрисовывания. Если оптимальных решений несколько, можно вывести любое из них.
Примечание
Решения, корректно работающие при M ≤ 2, будут оцениваться из 40 баллов.
Примеры
Входные данные
10 2 19 56 9 2
Выходные данные
375 5 10 9 8 7 6 5 1 2 3 4 5
#1344
Темы:
[Быстрая сортировка]
[Элементарная геометрия]
ограничение по времени на тест
0.1 second;
ограничение по памяти на тест
64 megabytes
На плоскости задано такое множество из N многоугольников, что выполняются следующие условия:
- никакие два многоугольника не имеют общих точек;
- для каждого i –го многоугольника существует Pi многоугольников, внутри которых он находится, и N-1-Pi многоугольников, которые находятся внутри его, 0 ≤Pi≤N-1.
Напишите программу, которая для каждого многоугольника выдает количество многоугольников, внутри которых он находится.
Входные данные
Первая строка входного файла содержит целое число N — количество многоугольников, 3≤N≤100000. Следующие N строк файла описывают N многоугольников. (i+1)–ая строка файла описывает i–ый многоугольник. Первое целое число Ci — количество вершин многоугольника, 3≤Ci≤20. Последующие Ci пар чисел — координаты вершин многоугольника в порядке его обхода. Координаты вершин — целые числа, принадлежащие диапазону от -2 000 000 000 до 2 000 000 000.
Выходные данные
Единственная строка выходного файла должна содержать N чисел: i–ое число строки должно быть Pi — количество многоугольников, внутри которых находится i–ый многоугольник.
Примеры
Входные данные
3 3 -2 1 8 9 12 1 3 7 5 6 3 7 4 4 4 3 7 7 9 3 1 2
Выходные данные
0 2 1
Выбрано
:
|