--->
90 задач
<---
Источники
#111491
Источники:
[
Личные олимпиады,
Всероссийская олимпиада школьников,
Региональный этап,
2013,
1 день,
Задача D
]
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
512 megabytes
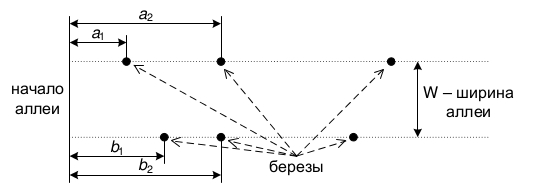
На краю деревни растет старая березовая аллея. Аллея имеет форму прямой полосы шириной \(W\) метров. Вдоль левой стороны аллеи растет \(N\) берез, а вдоль правой — \(M\) берез, при этом \(i\)-я береза с левой стороны аллеи находится на расстоянии \(a_i\) метров от начала аллеи, а \(j\)-я береза с правой стороны — на расстоянии \(b_j\) метров от начала аллеи.
Отдыхая в деревне прошедшим летом, один юный информатик обнаружил, что кору берез стали грызть зайцы. Чтобы защитить деревья от зайцев, мальчик решил окружить березы красной лентой (зайцы не любят красный цвет и не станут заходить на огражденную лентой территорию. К сожалению, в его распоряжении оказалась только лента длиной \(L\) метров, которую, к тому же, нельзя было разрезать. Единственное, что можно было делать в этом случае — окружить этой лентой как можно больше берез. При этом, чтобы сохранить аллею, необходимо окружить на каждой стороне аллеи хотя бы одну березу.
Требуется написать программу, которая по заданной длине ленты, ширине аллеи и положению берез на ней определяет максимальное число берез, которое можно окружить этой лентой. Считается, что березы представляются точками, толщиной берез и шириной ленты следует пренебречь.
Входные данные
Первая строка входного файла содержит два разделенных пробелом целых числа: длину ленты \(L\) и ширину аллеи \(W\) (\(1 \leq L \leq 2 \times 10^5\), \(1 \leq W \leq 10^4\)).
Вторая и третья строки описывают березы вдоль левой стороны аллеи. Вторая строка содержит число \(N\) — количество берез (\(1 \leq N \leq 2000\)), а третья строка содержит \(N\) различных целых чисел \(a_1\), \(a_2\), …, \(a_N\) (\(0 \leq a_i \leq 10^5\)), заданных по возрастанию.
Четвертая и пятая строки описывают березы вдоль правой стороны аллеи. Четвертая строка содержит число \(M\) — количество берез (\(1 \leq M \leq 2000\)), а пятая строка содержит \(M\) различных целых чисел \(b_1\), \(b_2\), …, \(b_M\) (\(0 \leq b_i ≤ 10^5\)), заданных по возрастанию.
Выходные данные
Выходной файл должен содержать одно целое число: максимальное количество берез, которое можно оградить заданной лентой.
Гарантируется, что если максимальное число берез, которое можно оградить лентой длины L, равно X, то нет способа оградить (X + 1) березу лентой длины (L + \(10^{-5}\)).
Система оценивания
Правильные решения для тестов, в которых 1 ≤ N + M ≤ 50, будут оцениваться из 30 баллов.
Правильные решения для тестов, в которых 1 ≤ N + M ≤ 500, будут оцениваться из 60 баллов.
Примеры
Входные данные
18 4 3 0 3 6 4 0 3 6 10
Выходные данные
5
Входные данные
5 3 1 0 1 0
Выходные данные
0
| Ограничение по времени, сек | 0.75 |
| Ограничение по памяти, мегабайт | 256 |
Министерство обороны Флатландии планирует построить новый военный полигон. Полигон должен иметь форму круга.
Поскольку генералы в министерстве волнуются о секретности проводимых на полигоне испытаний, он должен быть надежно защищен. Флатландия защищена сверху несколькими специальными силовыми щитами, каждый из них имеет форму прямоугольника со сторонами, параллельными осям координат. Генералы хотят выбрать такое место для полигона, где он был бы полностью защищен хотя бы двумя конкретными силовыми щитами (недостаточно, чтобы каждая точка просто была защищена хотя бы двумя щитами, должно быть два щита, каждый из которых защищает полигон полностью).
Конечно, генералы хотят построить полигон максимального возможного размера. Помогите им выбрать такое место для полигона, чтобы он имел максимальный возможный радиус.
Входные данные
Первая строка входного файла содержит число \(N\) — количество силовых щитов. Каждая из следующих N строк описывает силовой щит (\(1 \leq N \leq 200000\)). Описание представляет собой четверку координат: \(x_{min}\), \(y_{min}\), \(x_{max}\), \(y_{max}\). Все координаты целые и не превышают 100000 по абсолютной величине.
Выходные данные
Выведите три вещественных числа — координаты центра полигона и его радиус. Все числа следует выводить ровно с одним знаком после десятичной точки.
Если построить полигон невозможно, выведите “Impossible” на первой строке выходного файла.
Примеры тестов
Входные данные
4 0 0 2 3 1 -1 4 1 1 1 4 4 2 0 5 5
Выходные данные
3.0 2.0 1.0
Входные данные
1 0 0 1 1
Выходные данные
Impossible
Входные данные
2 0 0 3 3 0 0 3 3
Выходные данные
1.5 1.5 1.5
Решения, работающие при \(1 \leq N \leq 5 000\), будут набирать не менее 50 баллов
#111636
Источники:
[
Личные олимпиады,
Всероссийская олимпиада школьников,
Заключительный этап,
2013,
1 день,
Задача D
]
История Татаро-монгольского ханства богата на правителей. Каждый из N правителей принадлежал к одной из двух династий, причём власть часто переходила от одной династии к другой. Каждое восхождение правителя на престол отмечалось праздником, проводимым 26 марта. В летописях зафиксированы годы проведения этих праздников, причем известно, что правители первой династии устраивали для народа праздник кумыса, а второй — праздник мёда.
На конференции по истории Татаро-монгольского ханства каждый из S учёных предложил свою версию толкования летописи. А именно, i-й историк утверждал, что от каждого праздника кумыса до следующего праздника кумыса проходило не менее KLi лет, но не более KRi лет, в то время как от каждого праздника мёда до следующего праздника мёда проходило не менее MLi лет, но не более MRi лет.
Каждой предложенной версии может соответствовать несколько распределений правителей по династиям. Ученые договорились считать показателем сомнительности распределения число переходов власти к представителю той же самой династии.
Требуется написать программу, которая найдёт распределение, соответствующее хотя бы одной из версий и имеющее наименьший показатель сомнительности, а также версию, которой оно соответствует.
Входные данные
В первой строке входного файла записано число N (2 ≤ N ≤ 200 000) — количество праздников в летописи. Следующая строка содержит целые числа X1, X2, ..., XN (1 ≤ X1 ≤ X2 ≤ ... ≤ XN ≤ 109) — годы проведения праздников.
В третьей строке записано число учёных S (1 ≤ S ≤ 50). В каждой из последующих S строк записаны четыре натуральных числа KLi, KRi, MLi, MRi (1 ≤ KLi ≤ KRi ≤ 109), (1 ≤ MLi ≤ MRi ≤ 109).
Выходные данные
Первая строка выходного файла должна содержать числа P и Q, где P — номер учёного, версии которого соответствует распределение с наименьшим показателем сомнительности, а Q — показатель сомнительности этого распределения.
Вторая строка должна состоять из N цифр 1 и 2, записанных без пробелов, означающих приход к власти представителя первой или второй династии соответственно. Если существует несколько решений с наименьшим показателем сомнительности Q, выведите любое из них.
В случае, если ни в одной из версий учёных не существует способа распределения периодов правления между династиями так, чтобы не нарушались ограничения на промежутки времени между праздниками, выходной файл должен содержать единственное число 0.
Примечание
Данная задача содержит шесть подзадач. Для оценки каждой подзадачи используется своя группа тестов. Баллы за подзадачу начисляются только в том случае, если все тесты из этой группы пройдены.
- Тесты из условия. Подзадача оценивается в 0 баллов.
- 2 ≤ N ≤ 15, 1 ≤ S ≤ 10. Подзадача оценивается в 20 баллов.
- 2 ≤ N ≤ 2000, 1 ≤ S ≤ 50, N × S ≤ 2000. Подзадача оценивается в 20 баллов.
- 2 ≤ N ≤ 10 000, 1 ≤ S ≤ 50, N × S ≤ 10 000. Подзадача оценивается в 20 баллов.
- 2 ≤ N ≤ 200 000, 1 ≤ S ≤ 50, N × S ≤ 200 000. Подзадача оценивается в 20 баллов.
- 2 ≤ N ≤ 200 000, 1 ≤ S ≤ 50. Подзадача оценивается в 20 баллов.
Примеры
Входные данные
3 1 2 3 1 1 1 1 1
Выходные данные
1 1 211
Входные данные
4 1 6 9 13 2 1 2 2 3 6 7 3 3
Выходные данные
0
Входные данные
5 3 6 8 9 10 2 2 3 1 1 1 4 1 10
Выходные данные
2 0 21212
#111744
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
256 megabytes
Вася работает подмастерьем в известной студии. Недавно ему поручили помогать молодому, но подающему большие надежды художественному декоратору заборов и изгородей Витезславу Смолокурову. Миссия эта очень ответственная, и от ее выполнения зависит Васино будущее.
Стиль Смолокурова очень необычен, а его работы пользуются большим спросом. Процесс работы разделен на два этапа. На первом этапе Вася делает заготовку — длинный забор, который состоит из набора цветных вертикальных планок. На втором этапе Витезслав приступает к работе.
Для того, чтобы придать забору более спокойный и гармоничный вид, он несколько раз производит следующую операцию: выбирает некоторый цвет и отрезок, после чего перекрашивает этот отрезок забора в выбранный цвет. По своей творческой натуре, Смолокуров может в корне менять концепцию узора по нескольку раз за час, поэтому иногда он перекрашивает одну и ту же планку несколько раз. Кроме того, Витезслав не хочет, чтобы какой-то узор повторялся слишком часто. Для того, чтобы избежать этого, он иногда проверяет, не совпадает ли один отрезок забора с другим.
Несложно догадаться, что и перекрашивание, и проверки осуществляет Вася. Работа эта не самая простая, поэтому Вася просит ему помочь хотя бы с проверками на совпадение.
Входные данные
Первая строка входного файла содержит одно целое число n — количество планок в заборе (1 ≤ n ≤ 100 000). Вторая строка содержит n целых чисел, разделенных пробелами — цвета соответствующих планок.
Третья строка входного файла содержит одно целое число m — количество сравнений и перекрашиваний (1 ≤ m ≤ 100 000). Следующие m строк содержат описания заданий, который Вася получает от Витезслава: четыре целых числа q, l, r и k.
В случае перекрашивания q = 0. Эта запись означает перекрашивание всех планок с l по r включительно в цвет k (1 ≤ l ≤ r ≤ n). В запросе на сравнение q = 1. Эта запись означает сравнение кусков забора длины k начиная с позиций l и r соответственно (1 ≤ l, r ≤ n - k + 1, k > 0).
Все числа во входном файле положительные и не превышают 100 000.
Выходные данные
Выведите одну строку: для каждого запроса на сравнение выведите ‘+’ в случае совпадения соответствующих кусков забора и ‘-’ в противном случае.
Примеры
Входные данные
7 1 2 1 3 1 2 1 3 0 4 5 2 1 3 1 2 1 3 1 3
Выходные данные
+-
Входные данные
2 1 2 5 1 1 2 1 0 2 2 1 1 1 2 1 0 1 2 3 1 1 1 2
Выходные данные
-++
#111777
ограничение по времени на тест
0.5 second;
ограничение по памяти на тест
64 megabytes
Задана последовательность из n чисел a1, a2, ..., an. Подпоследовательностью длины k этой последовательности называется набор индексов i1, i2, ..., ik, удовлетворяющий неравенствам 1 ≤ i1 < i2 < ... < ik ≤ n. Подпоследовательность называется возрастающей, если выполняются неравенства ai1 < ai2 < ... < aik.
Необходимо найти число возрастающих подпоследовательностей наибольшей длины заданной последовательности a1, ... ,an. Так как это число может быть достаточно большим, необходимо найти остаток от его деления на 109 + 7.
Входные данные
Первая строка входного файла содержит целое число n (1 ≤ n ≤ 105). Вторая строка входного файла содержит n целых чисел: a1, a2, ... ,an. Все ai не превосходят 109 по абсолютной величине.
Выходные данные
В выходной файл выведите ответ на задачу.
Примеры
Входные данные
5 1 2 3 4 5
Выходные данные
1
Входные данные
6 1 1 2 2 3 3
Выходные данные
8
Выбрано
:
|