--->
30 задач
<---
Источники
#1759
Темы:
[Эвристические методы]
Источники:
[
Командные олимпиады,
Командные чемпионаты школьников Санкт-Петербурга по программированию,
2003,
Задача H
]
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes
Найдите квадрат числа, десятичная запись которого состоит из \(n\) единиц.
Входные данные
Входной файл содержит единственное число \(n\) (1 ≤ \(n\) ≤ \(10^5\)).
Выходные данные
Выведите искомый квадрат.
Примеры
Входные данные
2
Выходные данные
121
Входные данные
9
Выходные данные
12345678987654321
#1924
Темы:
[Динамическое программирование: два параметра]
[Условный оператор (if)]
[Эвристические методы]
Источники:
[
Личные олимпиады,
Всероссийская олимпиада школьников,
Региональный этап,
2010,
1 день,
Задача C
]
ограничение по времени на тест
4.0 second;
ограничение по памяти на тест
64 megabytes
Недавно на уроке информатики ученики одного из классов изучили булевы функции. Напомним, что булева функция \(f\) сопоставляет значениям двух булевых аргументов, каждый из которых может быть равен 0 или 1, третье булево значение, называемое результатом. Для учеников, которые выразили желание более подробно изучать эту тему, учительница информатики на дополнительном уроке ввела в рассмотрение понятие цепного вычисления булевой функции \(f\).
Если задана булева функция \(f\) и набор из \(N\) булевых значений \(a_1,a_2,\ldots,a_N\), то результат цепного вычисления этой булевой функции определяется следующим образом:
* если \(N=1\), то он равен \(a_1\);
* если \(N>1\), то он равен результату цепного вычисления булевой функции \(f\) для набора из \((N-1)\) булевого значения \(f(a_1,a_2),a_3,\ldots,a_N\), который получается путём замены первых двух булевых значений в наборе из \(N\) булевых значений на единственное булево значение — результат вычисления функции \(f\) от \(a_1\) и \(a_2\).
Например, если изначально задано три булевых значения: \(a_1=0\), \(a_2=1\), \(a_3=0\), а функция \(f\) — ИЛИ (OR), то после первого шага получается два булевых значения — (0 OR 1) и 0, то есть 1 и 0. После второго (и последнего) шага получается результат цепного вычисления, равный 1, так как 1 OR 0 = 1.
В конце дополнительного урока учительница информатики написала на доске булеву функцию \(f\) и попросила одного из учеников выбрать такие \(N\) булевых значений \(a_i\), чтобы результат цепного вычисления этой функции был равен единице. Более того, она попросила найти такой набор булевых значений, в котором число единиц было бы как можно бо́льшим.
Требуется написать программу, которая решала бы поставленную учительницей задачу.
Входные данные
Первая строка входного файла содержит одно натуральное число \(N\) (\(2\le N\le100\,000\)).
Вторая строка входного файла содержит описание булевой функции в виде четырёх чисел, каждое из которых — ноль или единица. Первое из них есть результат вычисления функции в случае, если оба аргумента — нули, второе — результат в случае, если первый аргумент — ноль, второй — единица, третье — результат в случае, если первый аргумент — единица, второй — ноль, а четвёртый — в случае, если оба аргумента — единицы.
Выходные данные
В выходной файл необходимо вывести строку из \(N\) символов, определяющих искомый набор булевых \(a_i\) с максимально возможным числом единиц. Если ответов несколько, требуется вывести любой из них. Если такого набора не существует, выведите в выходной файл фразу «No solution».
Пояснения к примерам
В первом примере процесс вычисления цепного значения булевой функции \(f\) происходит следующим образом: \(1011\to111\to01\to1\)
Во втором примере вычисление цепного значения булевой функции \(f\) происходит следующим образом: \(11111\to0111\to111\to01\to1\)
В третьем примере получить цепное значение булевой функции \(f\), равное 1, невозможно.
Примеры
Входные данные
4 0110
Выходные данные
1011
Входные данные
5 0100
Выходные данные
11111
Входные данные
6 0000
Выходные данные
No solution
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes
<з>Дан прямоугольник \(m \times n\), клетки которого раскрашены в три цвета. Можно выбрать квадрат \(2 \times 2\) и, если в нем какой-то цвет преобладает,
перекрасить весь этот квадрат \(2 \times 2\) в этот цвет.
Если в нем по две клетки двух цветов, то все его клетки можно
перекрасить в третий цвет. Требуется такими операциями
перекрасить весь прямоугольник в один цвет.
перекрасить весь этот квадрат \(2 \times 2\) в этот цвет.
Если в нем по две клетки двух цветов, то все его клетки можно
перекрасить в третий цвет. Требуется такими операциями
перекрасить весь прямоугольник в один цвет.
Входные данные
Числа \(m\), \(n\) (\(3 \le m, n \le 100\)) и раскрашенный прямоугольник.
Прямоугольник задается набором из \(m\) строк, в каждой из которых
\(n\) символов \(R\), \(G\) или
\(B\).
Выходные данные
Последовательность перекрашиваемых квадратов (не более \(10mn\) операций),
по одному перекрашиванию в строке. Каждое перекрашивание задается
парой чисел - номером строки и столбца левого верхнего квадрата в перекрашиваемом прямоугольнике.
Input
4 4
RBRR
GRGG
RRGB
GRRG
RBRR
GRGG
RRGB
GRRG
Output
1 1
1 2
1 3
3 1
2 2
2 3
3 3
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes
В этой задаче не будет идти речь о Бердяндии, о дорогах или авиарейсах. Здесь не будет надоевших монет. Речь пойдет о простой квадратной матрице.
В квадратную матрицу A порядка n были вписаны числа от 1 до n2, каждое по одному разу. Затем для каждого числа была записана пара чисел topi,j и lefti,j, где topi,j это количество чисел в столбце j стоящих выше числа Ai,j и одновременно больших него, а lefti,j это количество чисел в строке i стоящих левее числа Ai,j и одновременно больших него.
Вам заданы матрица top и left. Ваша задача состоит в нахождении возможной матрицы A, соответствующей входным данным.
Входные данные
В первой строке входного файла записано целое число n (1 ≤ n ≤ 600), где n это порядок искомой матрицы. Далее во входном файле записана пара матриц top и left, в виде n строк по n чисел в каждой строке. Матрицы разделены пустой строкой.
Выходные данные
В выходной файл выведите матрицу A в формате, аналогичном входным данным. Если решений несколько, то выведите любое. Если решения не существует, выведите единственное число 0.
Примеры
Входные данные
3 0 0 0 0 0 0 0 0 2 0 0 0 0 1 0 0 1 2
Выходные данные
1 2 6 5 3 7 9 8 4
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
256 megabytes
Юная любительница ювелирных изделий Октябрина к празднику 4-го ноября хочет подарить своей лучшей подруге Тракторине ожерелье из n черных и розовых жемчужин.
Чтобы ожерелье не было скучным, Октябрина хочет расположить жемчужины таким образом, чтобы как его ни повернуть, левая половина ожерелья не была симметрична правой. Более формально – у него не должно быть оси симметрии.
Ось симметрии делит ожерелье на непрерывные части, содержащие одинаковое число жемчужин. При этом, если ось проходит через какую-то жемчужину, то она относится к обеим частям, если же ось проходит между двух жемчужин, то эти жемчужины находятся в разных частях. Таким образом, следующие ожерелья имеют ось симметрии:
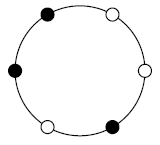
Ваша задача – помочь Октябрине найти необходимую расстановку жемчужин.
Входные данные
Первая и единственная строка входного файла содержит единственное число n
(2 ≤ n ≤ 1000) – требуемое количество жемчужин в ожерелье.
Выходные данные
Если искомой расстановки не существует, выведите в выходной файл единственное число –1,
иначе выведите n целых чисел – расстановку жемчужин. Розовой жемчужине соответствует число
0, черной – число 1.
Примечание.
Расстановка жемчужин в первом примере:
Примеры
Входные данные
6
Выходные данные
0 0 1 0 1 1
Входные данные
3
Выходные данные
-1
Выбрано
:
|