--->
30 задач
<---
Источники
Андрей популярный писатель-фантаст, он проводит мастер-классы для своих читателей. Наиболее популярным из них является Alien Communication Masterclass (ACM), на котором он учит как поступать в случае встречи с пришельцем или нахождении инопланетного артефакта.
Одна из лекций посвящена извлечению информации из инопланетных записей. Исследования Андрея базируется на математических формулах пришельцев, которые могут дать некоторые знания об организмах пришельцев (например, мы используем десятичную систему счисления потому что у нас 10 пальцев на верхних конечностях).
Предположим для простоты, что пришельцы используют те же самые цифры, что и мы и таким же образом трактуют сложение, вычитание, умножение, скобки и равенство.
Для своей лекции Андрей хочет найти пример равенства, которое выполняется в системах счисления с основаниями a1, a2, .., aN, но не выполняется в системах счисления с основаниями b1, b2, …, bM. Найдите для него пример такой формулы.
Входные данные
Первая строка входного файла содержит два целых числа N и M (1 ≤ N, M ≤ 8).
Вторая строка содержит N чисел a1, a2, .., aN
Третья строка содержит M чисел b1, b2, …, bM
Все числа ai и bi различны и лежат в пределах от 2 до 10.
Выходные данные
Вывод должен представлять собой корректное математическое равенство, которое выполняется в системах счисления с основаниями a1, a2, .., aN и не выполняется в системах с основаниями b1, b2, …, bM.
Равенство может содержать цифры от 0 до 9, знак плюс +, минус и унарный минус –, знак умножения *, скобки ( и ) и знак равенства =. Знак равенства должен быть ровно один.
Все пробельные символы будут проигнорированы при проверке. Количество непробельных символов не должно превышать 10000.
Примеры тестов
Входные данные
1 2
2
3 9
Выходные данные
(10 - 1) * (10 - 1) + 1 = 10
Входные данные
2 2
9 10
2 3
Выходные данные
2 + 2 = 4
Город Нью-Йорк практически парализован гигантским количеством пробок. Мэр Джулио Джулиани предложил новую схему движения по городским улицам. Все улицы по этому плану должны стать односторонними.
Город расположен на прямоугольном острове размером M на N квадратных футов. (M футов с юга на север и N футов с запада на восток. Город разделен на кварталы улицами, идущими с запада на восток и авеню, идущими с юга на север. Длина каждого из кварталов составляет 200 футов (строго говоря, это расстояние между двумя параллельными улицами, окружающими квартал). Улицы нумеруются с юга на север начиная с единицы. Авеню нумеруются с запада на восток также с единицы.
Одностороннее движение организовано так, как показано на рисунке.
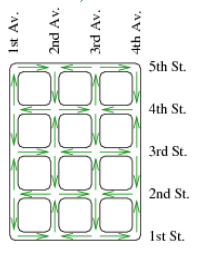
Мэр хочет проехать от одного перекрестка до другого. Определите минимальное расстояние между этими перекрестками. Для простоты можно игнорировать расстояние пройденное на перекрестках, т.е. расстояние пройденное вдоль квартала составляет ровно 200 футов.
Входные данные
Входной файл состоит из 4 строк
Первая строка содержит число M (400 ≤ M ≤ 1000000). Следующая строка содержит число N (400 ≤ N ≤ 1000000). Оба числа делятся на длину квартала. Следующие две строки описывают начальный и конечный перекресток. Каждое описание перекрестка задается так:
m Av., n St.
Например,
1st Av., 5th St.
Выходные данные
Выведите минимальное расстояние между перекрестками.
Примеры
Входные данные
800 600 1st Av., 1st St. 2nd Av., 3rd St.
Выходные данные
1000
#2975
Темы:
[Эвристические методы]
[Условный оператор (if)]
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
256 megabytes
На днях Алиса делала уборку в своей комнате и нашла дневник, который вела в начальной школе. Там она с удивлением обнаружила запись о том насколько ее поразило то, что \(2 + 2 = 2 \cdot 2\). Невероятно, умножение и сложение дают один и тот же результат!
Эта запись натолкнула Алису на следующую задачу: пусть целые заданы числа \(a\) и \(b\). Сколько различных значений в наборе чисел
| \(a + b\), | \(\;a - b\), | \(\;a \cdot b\), | \(\;a / b\), | \(\;a^b\), |
| \(b + a\), | \(\;b - a\), | \(\;b \cdot a\), | \(\;b / a\), | \(\;b^a\). |
Деление происходит без округления, результат деления может не быть целым числом. Если какое-либо выражение из этого набора некорректно, то Алиса его не рассматривает. Некорректными считаются деление на ноль и возведение нуля в неположительную степень.
Входные данные
Первая строка входного файла содержит целые числа \(a\) и \(b\), разделенные пробелом (\(|a|, |b| \le 10^9\)).
Выходные данные
Выведите в выходной файл количество различных чисел в приведенном наборе.
#3590
Источники:
[
Командные олимпиады,
Московская командная олимпиада,
9-11 классы,
2011,
Лига Б,
Задача C
]
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes
Игра «Палиндромика» набирает все большую популярность в казино Рулеттенбурга. Правила «Палиндромики» довольно просты: в начале игры на листок записывается строка и игроки поочередно стирают первый или последний символ. Побеждает игрок, перед ходом которого строка представляет собой палиндром. Палиндромом называется строка, которая читается одинаково как слева направо, так и справа налево.
Алексей Иванович — азартный игрок, однако вместо участия в игре предпочитает делать ставки. Ему удалось узнать, какая строка будет предложена для игры. Алексею Ивановичу предсказать исход игры при оптимальных действиях обоих игроков не под силу. За помощью он обратился к вам.
Входные данные
В единственной строке входного файла содержится строка, предложенная игрокам. Строка состоит из маленьких латинских букв. Длина строки не превышает 250 символов.
Выходные данные
Выведите номер игрока, который победит в игре (число 1 или 2) при оптимальной игре каждого из игроков.
Примеры
Входные данные
3 uho
Выходные данные
1
Входные данные
6 ababab
Выходные данные
2
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
256 megabytes
У Элли есть \(N\) овец на пастбище. У неё также есть \(K\) гончих собак, которые охраняют овец от волков. Опасность для каждой овцы можно вычислить как расстояние до ближайшей собаки - чем оно меньше, тем лучше. Опасность для стада можно вычислить как сумму этих расстояний для каждой овцы. Мы считаем пастбище плоской поверхностью, а овец - точками на плоскости.
Элли задаётся вопросом, как расположить своих собак (которые также являются точками на плоскости), чтобы сумма минимальных расстояний от каждой овцы до ближайшей собаки была как можно меньше. Другими словами, вам даны \(N\) точек, и вам следует разместить \(K\) новых точек таким образом, чтобы сумма минимальных расстояний от каждой из заданных точек до ближайшей новой была как можно меньше. Напишите программу для решения этой задачи.
Входные данные
В первой строке стандартного ввода даны натуральные числа \(N\) и \(K\) - количество овец и количество собак соответственно. В каждой из следующих \(N\) строк даны два целых числа \(X_i\) и \(Y_i\) - координаты \(i\)-й овцы.
Выходные данные
Выведите \(K\) пар вещественных чисел - координаты собак, разделенные пробелом, с точностью до шестой цифры после десятичной точки. Допускается размещение собаки в той же точке, где и овца.
Система оценки
За каждый тест вашему решению будут начисляться баллы, равные \(round(min(1, (authorScore / yourScore))^4 * testScore)\), где \(authorScore\) - это результат, найденный решением жюри, \(yourScore\) - результат вашего решения, и \(testScore\) - максимальная оценка для данного теста.
Примеры
Входные данные
7 2 1 2 1 4 2 5 3 2 4 4 5 6 6 5
Выходные данные
1.750000 3.250000 5.000000 5.000000
Выбрано
:
|