Назовём строкой последовательность из маленьких букв латинского алфавита. Строкой, например, является пустая последовательность, слово «aabaf» или бесконечная последовательность букв «a».
i-ый суффикс Si строки S — это строка S, из которой вырезаны первые i букв; так, для строки S = aabaf суффиксы будут такими:
- S0 = aabaf
- S1 = abaf
- S2 = baf
- S3 = af
- S4 = f
- S5 = S6 = S7 = ... = «»
Суффиксы определены для всех i \(\ge\) 0.
Циклическое расширение S * конечной строки S — это строка, полученная приписыванием её к самой себе бесконечное количество раз. Так,
- S * = S * 0 = aabafaabafaabafaa...
- S * 1 = abafabafabafabaf...
- S * 2 = bafbafbafbafbafb...
- S * 3 = afafafafafafafaf...
- S * 4 = ffffffffffffffff...
- S * 5 = S * 6 = S * 7 = ... = ""
По заданной строке S выясните, сколько её суффиксов Si имеют такоей же циклическое расширениe, как и строка S, то есть количество таких i, что S * = S * i.
В первой и единственной строке входного файла задана строка S, состоящая из не менее, чем одной, и не более, чем 100000 маленьких латинских букв 'a'-'z'.
Выведите в первую строку выходного файла одно число — количество суффиксов строки S, имеющих такое же циклическое расширение, как и она сама.
aa
2
ab
1
qqqq
4
xyzzyxy
1
Дана строка S. Назовем ее подстрокой строку с i-го по j-й символ (i ≤ j). Ваша задача — посчитать количество различных подстрок данной строки.
Во входном файле находится одна строка S, состоящая не более, чем из 200000 символов. Все символы в строке — маленькие латинские буквы.
В выходной файл выведите единственное число — количество различных подстрок заданной строки. Гарантируется, что в данных тестах ответ не более 1018.
aaba
8
Привидение Петя любит играть со своими кубиками. Он любит выкладывать их в ряд и разглядывать свое творение. Однако недавно друзья решили подшутить над Петей и поставили в его игровой комнате зеркало. Ведь всем известно, что привидения не отражаются в зеркале! А кубики отражаются. Теперь Петя видит перед собой N цветных кубиков, но не знает, какие из этих кубиков настоящие, а какие — всего лишь отражение в зеркале. Помогите Пете! Выясните, сколько кубиков может быть у Пети. Петя видит отражение всех кубиков в зеркале и часть кубиков, которая находится перед ним. Часть кубиков может быть позади Пети, их он не видит.
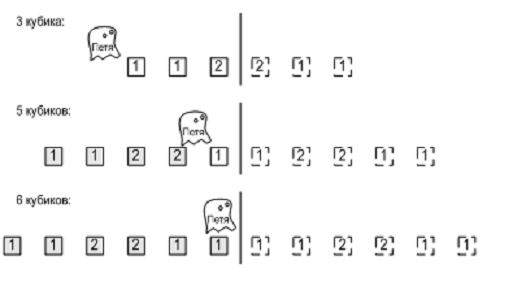
Первая строка входного файла содержит число N ( 1 ≤ N ≤ 1000000 ) и количество различных цветов, в которые могут быть раскрашены кубики — M ( 1 ≤ M ≤ 1000000 ). Следующая строка содержит N целых чисел от 1 до M — цвета кубиков.
Выведите в выходной файл все такие K , что у Пети может быть K кубиков
6 2 1 1 2 2 1 1
3 5 6
Известно, что в солнечной системе есть 8 планет и один планетоид. Мало кто знает, что ещё есть секретная планета, населенная медведями. Именно туда ассоциация Savez отправляет бравого генерала Хенрика для изучения медведей. Выяснилось, что медведи умеют телепортироваться. Расчётливый генерал Хедрик решил завербовать их в свою армию.
У одного медведя есть N строк (обозначим i -ю из них x i ). Исследования показывают, что количество раз, которое может телепортироваться медведь равно длине наибольшей подпоследовательности этих строк, удовлетворяющей такому правилу: строки x i и x j ( i < j ) могут принадлежать одной такой последовательности, если x i является и префиксом, и суффиксом x j .
Помогите уставшему от долгого полёта генералу Хендрику определить, сколько телепортаций сможет сделать данный медведь.
В первой строке содержится одно целое число N – количество строк, которые есть у медведя. В последующих N строках содержатся сами эти строки. Входной файл содержит не более двух миллионов символов.
Выведите одно число – ответ на вопрос любопытного генерала Хендрика.
В первом примере наибольшая последовательность A -> AA -> AAA В третьем примере наибольшая последовательность A -> A -> A или B -> B -> B
5 A B AA BBB AAA
3
5 A ABA BBB ABABA AAAAAB
3
6 A B A B A B
3
Недавно произошла утечка информации из мега-популярной социальной сети. Среди конфиденциальной информации, попавшей в сеть, оказались и пароли всех пользователей.
Михаил, школьник, увлекающийся компьютерной безопасностью, нашёл произошедший инцидент очень интересным. Экспериментируя с социальной сетью, он нашёл ещё одну брешь в её системе безопасности! Войти в аккаунт можно, если ввести строку, содержащую настоящий пароль от аккаунта как подстроку. Например, если пользователь, чей пароль « abc » введёт « abc », « abcd » или « imaabcnema », у него успешно получиться авторизоваться в системе, но у него не получится если он введёт « axbc ».
Миша хочет узнать, сколько существует упорядоченных пар пользователей таких, что если первый пользователь введёт пароль, то он сможет войти в аккаунт второго пользователя.
В первой строчке вводится одно целое число N — число пользователей ( 1 ≤ N ≤ 20 000 ). В следующих N строках вводятся пароли пользователей, по одному в строке. Пароль содержит от 1 до 10 маленьких букв латинского алфавита.
Выведите единственное число — количество пар, которое интересует Мишу.
Решение, правильно работающее при 1 ≤ N ≤ 2 000 , будет оцениваться в 40 баллов.
Во втором примере первый пользователь может войти в аккаунт второго и третьего пользователя, а второй пользователь — в аккаунт первого и третьего пользователя.
3 aaa aa abb
1
3 x x xy
4
5 mir mirta ta ir t
6