Король Байтазар считает, что Байтотия — земля, полная красивых достопримечательностей — должна привлечь множество туристов, которые должны потратить много денег, которые в конечном счете должны найти свой путь в королевскую казну. Но реальность далека от мечты. Поэтому король поручил своему советнику изучить этот вопрос. Советник выяснило, что иностранцы держаться подальше от Байтотии из-за ее плохой дорожной сети. В Байтотии \(n\) городов соединенных \(m\) двусторонними дорогами. Не гарантируется, что от каждого города можно добраться от любого другого города. Советник отметил, что нынешний дорожная сеть не позволяет делать длительные путешествия. А именно, где бы вы не начали поездку, невозможно посетить более 10 городов не прохождения через какой-то город два раза. Из-за ограниченных средств в казне, новые дороги построить нельзя. Вместо этого, Байтазар решил создать сеть туристическо-информационных пунктов (ТИП), которые будут рекламировать короткие путешествия. Для каждого города должен быть ТИП либо в нем, либо в одном из городов, непосредственно связанных с ним дорогой. Кроме того, известна стоимость строительства ТИПа в каждом из городов. Помогите королю найти самый дешевый спосою построить ТИПы, так, чтобы это условие удовлетворялось.
Первая строка стандартного ввода содержит два целых числа \(n\) и \(m\) (\(2 \le n \le 20000, 0 \le m \le 25000\)), которые задают количество городов и дорог в Байтотии соответственно. Города нумеруются от \(1\) до \(n\). Вторая строка содержит целые числа \(c_i\) (\(0 \le ci \le 10000\)) — стоимости строительства ТИПов в городах. Затем идет описание дорожной сети. i-я строка содержит два целых числа \(a_i, b_i\), которые указывают, что города \(a_i\) и \(b_i\) связаны дорогой. Существует не более одной дороги между любой парой городов.
Выведите одно целое число — общую стоимость строительства всех ТИПов.
Подзадача 1 (22 балла): \(1 \le n, m \le 20\)
Подзадача 2 (78 баллов): Без дополнительных ограничений. Оценивается потестово. (6 баллов за тест)
6 6 3 8 5 6 2 2 1 2 2 3 1 3 3 4 4 5 4 6
7
Центр Гдынии расположен на острове посередине реки Кацза. Каждое утро тысячи машин едут из жилых районов на западном берегу в индустриальные на восточном.
Остров можно представить в виде прямоугольника \(A\times B\) со сторонами, параллельными осям координат, углами \((0, 0)\) и \((A, B)\).
На острове есть \(n\) перекрёстков, пронумерованных натуральными числами от \(1\) до \(n\). Перекрёсток номер \(i\) имеет координаты \((x_i, y_i)\). Если координаты какого-то перекрёстка имеют вид \((0, y)\), то он находится на западном берегу, если \((A, y)\) - на восточном. Перекрёстки соединены дорогами, каждая - отрезок на плоскости, они не пересекаются (кроме концов). Дороги бывают односторонними и двусторонними. Нет никаких мостов и туннелей! Некоторые дороги могут идти по краям прямоугольника.
Поскольку плотность траффика растёт, мэр города нанял Вас (кого же ещё) проверить, достаточно ли текущей сети дорог. Он попросил написать программу, которая по карте города определит для каждого перекрёстка на западном берегу, сколько из него достижимых на восточном.
В первой строке входных данных дано четыре целых числа \(n\), \(m\), \(A\) и \(B\) (\(1\leq n\leq 300 000\), \(0\leq m\leq 900 000\), \(1\leq A\leq 10^9\), \(1\leq B\leq 10^9\). Это количества перекрёстков, дорог и размеры города, соответственно.
В каждой из следующих \(n\) строк есть два целых числа \(x_i\), \(y_i\) (\(0\leq x_i\leq A\), \(0\leq y_i\leq B\)), описывающих координаты перекрёстка номер \(i\). Перекрёстки не совпадают.
Следующие \(m\) строк описывают дороги, каждая одну. Это описание состоит из трёх чисел: \(c_i\) - номер перекрёстка, откуда (\(1\leq c_i\leq n\)), \(d_i\) - куда (\(1\leq d_i\leq n\)), \(k_i\in\{1, 2\}\) - тип дороги (сколькосторонняя). Разные дороги соединяют разные неупорядоченные пары перекрёстков.
Есть хотя бы один перекрёсткок на западном берегу, из которого можно добраться хотя бы в один на восточном по дорогам.
Выведите для каждого перекрёстка на западном берегу в своей строчке количество достижимых из него перекрёстков на восточном берегу.
Выводите в порядке уменьшения \(y\)-координаты.
1. (30 баллов) \(n, m\leq 6 000\).
2. (70 баллов) \(n\leq 300 000\), \(m\leq 900 000\).
5 3 1 3 0 0 0 1 0 2 1 0 1 1 1 4 1 1 5 2 3 5 2
2 0 2
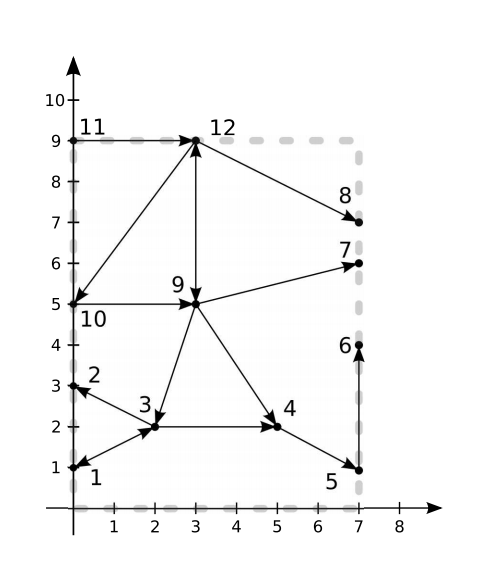
12 13 7 9 0 1 0 3 2 2 5 2 7 1 7 4 7 6 7 7 3 5 0 5 0 9 3 9 1 3 2 3 2 1 3 4 1 4 5 1 5 6 1 9 3 1 9 4 1 9 7 1 9 12 2 10 9 1 11 12 1 12 8 1 12 10 1
4 4 0 2
Фермер Джон спрятал ключи от трактора в сейфе. Коровы пытаются взломать этот сейф. Сейф защищён сложной парольной системой.
Она организована как подвешенное за вершину 0 дерево из \(n\) (\(1 \le n \le 20000\)) вершин, каждая из которых требует цифру от \(0\) до \(9\). Вершины пронумерованы от \(0\) до \(n - 1\).
Единственная информация, которой владеют коровы – что определённые последовательности длины \(5\) не появляютя на путях в этом дереве начиная с каких-то стартовых позиций при движении вверх по дереву.
По заданным \(m\) (\(0 \le m \le 50000\)) последовательностям длины \(5\), вместе с их стартовой позицией в дереве помогите коровам вычислить сколько паролей будет не подходить.
Вы должны выводить свой ответ по модулю \(1234567\).
Первая строка ввода содержит два разделённых пробелом целых числа, \(n\) и \(m\) (\(1 \le n \le 20000, 0 \le m \le 50000\)) - количество вершин в дереве и количество запрещённых последовательностей соответственно.
В последующих \(i\) строках находится описание дерева. Строка \(i + 1\) содержит одно целое число \(p[i]\), означающее родителя вершины \(i\) в дереве (\(0 \le p[i] \lt i\)).
В последующих \(m\) строках находится описание запрещённых последовательностей. Строка \(n + i\) содержит два целых числа \(v_i\) и \(s_i\), разделенные пробелом - стартовую вершину последовательности, и строку из \(5\) цифр, которая не встретится в шифре начиная с вершины \(v_i\) если двигаться вверх по дереву (\(0 \le v_i \lt n\)) соответственно.
Гарантируется, что корень дерева находится не менее чем в 4 шагах от \(v_i\).
Выведите единственное целое число – количество неподходящих конфигураций цифр по модулю \(1234567\).
Подзадача 1 (10 баллов): \(1 \le n \le 15, 0 \le m \le 15\)
Подзадача 2 (15 баллов): \(1 \le n \le 1000, 0 \le m \le 2000\)
Подзадача 3 (20 баллов): \(1 \le n \le 1000, 0 \le m \le 50000\)
Подзадача 4 (55 баллов): \(1 \le n \le 20000, 0 \le m \le 50000\)
6 2 0 1 2 3 3 4 01234 5 91234
19
Мислав и Мирко разработали новую игру под названием повороты.
Сначала Мирко выбирает последовательность чисел длины \(n\) и число \(k\) и разбивает последовательность на секции, каждая из которых содержит \(k\) чисел (\(n\) делится на \(k\)). Первая секция содержит первые \(k\) позиций в последовательности, вторая секция содержит последующие \(k\) позиций в последовательности и так далее.
После этого Мирко начинает применять различные операции на данной последовательности. Есть два типа операций:
1. Совершить циклический сдвиг элементов последовательности чисел в каждой секции на \(x\) влево или вправо.
2. Совершить циклический сдвиг элементов последовательности чисел целиком на \(x\) влево или вправо.
Заметим, что операция типа 2 может изменить то, к какой секции принадлежит какое число.
После применения всех операций, Мирко сообщает Миславу получившуюся последовательность и применённые операции. Задача Мислава заключается в том, чтобы восстановить исходную последовательность. Он попросил вас о помощи.
Первая строка ввода содержит три целых числа \(n\), \(k\), \(q\) (\(1 \le n \le 100000; 1 \le k \le 100000; 1 \le q \le 100000\)) - длину последовательности, длину каждой секции и количество применённых операций соответственно.
Последующие \(q\) строк содержат описание выполненных операций. Каждая из последующих \(q\) строк содержит два целых числа \(a\) (\(1 \le a \le 2\)) - тип операции, и \(x\) (\(-100000 \le x \le 100000\)) - число позиций, на которое был произведен циклический сдвиг. Если число \(x\) отрицательно, надо производить циклический сдвиг на \(|x|\) элементов влево, иначе - на \(|x|\) элементов вправо.
Последняя строка содержит \(n\) целых чисел, \(i\)-е из которых - это число, которое будет стоять на \(i\)-й позиции после выполнения операций из условия.
В единственной строке выведите \(n\) чисел - исходную последовательность.
Подзадача 1 (15 баллов): (\(n \le 100\))
Подзадача 2 (20 баллов): (\(k \le 100\))
Подзадача 3 (65 баллов): без дополнительных ограничений
4 2 2 2 2 1 1 3 2 1 0
0 1 2 3
8 4 4 1 3 1 15 1 -5 2 -1 6 10 14 19 2 16 17 1
6 10 14 1 2 16 17 19
9 3 5 1 1 2 -8 2 9 1 1 2 -4 3 1 8 7 4 5 2 6 9
5 3 6 9 7 1 8 2 4
Недавно в Байтландии изобрели Битовый Поляризационный Магнит. Если его применить, каждая дорога в Байтландии станет односторонней. Это будет очень плохо, ведь в Байтландии дороги образуют дерево — от каждого города до каждого ровно один путь. В зависимости от того, в какую сторону окажется ориентирована каждая дорога, различные города станут недостижимы друг из друга. Теперь ученые решили выяснить, насколько плохо будет жить в Байтландии, если применить БПМ. Определите минимальное и максимальное количество пар городов, что из первого по прежнему можно будет добраться до другого после применения магнита.
Первая строка содержит число \(n\) — число городов в Байтландии (\(1 \le n \le 250000\)). Следующая \(n - 1\) строка описывают дороги, каждая дорога описывается двумя различными числами от \(1\) до \(n\) — номерами городов, которые он соединяет. От каждого города можно добраться до любого другого.
Выведите два числа: минимальное и максимальное число искомых пар городов.
Подзадача 1 (10 баллов): \(1 \le n \le 15\)
Подзадача 2 (15 баллов): \(1 \le n \le 100\)
Подзадача 3 (15 баллов): \(1 \le n \le 3000\)
Подзадача 4 (10 баллов): \(1 \le n \le 10000\)
Подзадача 5 (35 баллов): \(1 \le n \le 60000\)
Подзадача 6 (15 баллов): Без дополнительных ограничений
4 1 2 1 3 1 4
3 5
8 1 2 2 3 3 4 4 5 5 6 6 7 7 8
7 28