Домик черепахи расположен в начале прямой узкой грядки, на которой должны прорасти одуванчики – ее любимое лакомство. И вот черепахе приснился вещий сон. Из него она узнала, что наконец-то после полуночи начнут расти одуванчики. Ей даже приснилось, в какой момент времени, и в какой точке грядки вырастет каждый одуванчик. Ровно в полночь черепаха выползла из домика, чтобы съесть все одуванчики и до следующей полуночи вернуться домой.
Черепаха может ползти со скоростью, не превосходящей величины vmax. Одуванчик она съедает, остановившись на время d. Если одуванчик начать есть, но не доесть до конца, то он засыхает, поэтому его надо съедать за один прием. Одуванчики прорастают тем позже, чем дальше они расположены от начала грядки. В одной точке не могут прорастать несколько одуванчиков, а также несколько одуванчиков не могут прорастать в один момент времени.
Требуется определить, в какой момент времени черепаха сможет вернуться домой, съев все одуванчики и затратив на путешествие наименьшее время.
В 1-й строке входного файла находятся 2 целых числа, разделенные пробелом: vmax (в см/мин) и d (в минутах), 0 < vmax ≤ 200, 0 ≤ d ≤ 500.
Во 2-й строке находится число N – количество одуванчиков (в штуках). 0 ≤ N ≤ 1400 при d = 0, в противном случае 0 ≤ N ≤ 200.
В каждой из последующих N строк расположены: целое число xi – расстояние от одуванчика до начала грядки (в сантиметрах), 0 ≤ xi ≤ 32767, и через пробел ti – момент прорастания одуванчика (в формате hh:mm). Пары приведены в порядке возрастания расстояний.
Выходной файл должен содержать момент времени возвращения черепахи домой (в формате hh:mm), округленный до целых минут в большую сторону.
Примечания
1. В часе – 60 минут, в сутках – 24 часа.
2. Время в сутках изменяется от 00:00 до 23:59.
3. Можете считать, что черепаха не меняет направления движения до тех пор, пока не доползет до последнего одуванчика.
3 1 1 100 00:01
01:08
Даша имеет \(n\) ювелирных украшений. Каждое украшение имеет стоимость \(w_i\) и значимость для Даши \(v_i\). В связи с финансовым кризисом Даша решила продать некоторые украшения и сохранить только \(k\) из имеющихся. Чтобы решить, что именно сохранить, Даша вводит параметр важности для набора из выбранных \(k\) украшений, который вычисляет по следующей формуле:
\(\frac{\sum_{j=1}^k v_i}{\sum_{j=1}^k w_i}\)Даша решает сохранить такие \(k\) украшений, для которых параметр важности будет максимально возможным. Помогите ей правильно выбрать украшения.
Первая строка ввода содержит числа \(n\) – количество ювелирных изделий у Даши и \(k\) – количество ювелирных изделий, которые планируется оставить \( (1 \leq k \leq n \leq 100\,000) \).
В следующих \(n\) строках содержатся по два числа – \(v_i\) и \(w_i (0 \leq v_i \leq 10^6, 1 \leq w_i \leq 10^6\), обе суммы всех значений \(v_i\) и \(w_i\) не превосходят \(10^7\) каждая).
Выведите \(k\) чисел – номера ювелирных украшений, которые следует оставить. Если существует несколько решений, то выведите любое из них.
3 2 1 1 1 2 1 3
1 2
Наиболее известная игра, дошедшая до нас из Японии – это Судоку. Новая игра должна затмить ее славу. Про нее известно следующее. Нам дан квадрат, разделенный сеткой на n×n клеток, а каждая клетка содержит картинку одного из k типов. Игрок должен переместить их, чтобы получить максимально возможное число одинаковых первых рядов (два ряда считаются одинаковыми, если оба заполнены одинаковыми картинками и в одинаковом порядке). По виду таблицы определите, сколько одинаковых рядов в ней можно сложить (если менять картинки как угодно).
Например, если нам дана такая таблица:
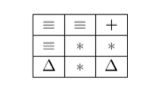
одно из результирующих состояний в игре будет
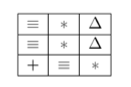
Первая строка входных данных содержит два числа n (\(1\leq n \leq 40000\)) и k (\(1 \leq k \leq 50000\)). Каждая из следующих k строк содержит число картинок в таблице каждого из k типов. Все числа больше 0, их сумма в точности равна \(n^2\).
Выведите в первой строке максимальное количество одинаковых рядов, которые можно построить из этих картинок. В следующих n строках выведите содержание таких рядов: в каждой строке должно находиться одно число – номер соответствующей картинке в порядке ее появления во входных данных. Если решений несколько, выведите любое из них.
3 4 3 3 2 1
2 1 2 3
Роман коллекционирует числа, кажущиеся ему интересными. Например, сейчас он считает интересным положительные числа, запись которых в системе счисления с основанием k заканчивается нечетным числом нулей. Например, при k = 2 такими числами являются 210 = 102, 2410 = 110002.
Для того, чтобы пополнить свою коллекцию, Роман хочет найти n-ое в порядке возрастания такое число. Поскольку n он взял достаточно большим, то вручную у него это сделать не получается. Помогите Роману — напишите программу, которая найдет число, которое нужно ему для пополнения коллекции.
Первая строка входного файла содержит два целых числа (1 ≤ n ≤ 1015, 2 ≤ k ≤ 10).
В выходной файл выведите n-ое в порядке возрастания число, запись которого в системе счисления с основанием k заканчивается на нечетное число нулей. Это число необходимо вывести в десятичной системе счисления.
1 2
2
10 10
110
Трамвайная линия имеет вид прямой. Петя живет в N трамвайных остановках от метро. Метро находится у нулевой остановки, в точке с координатой 0.
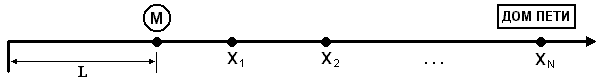
Выходя из метро, Петя хочет попасть домой как можно быстрее, но он очень не любит ждать трамвай на остановке. Поэтому, если, подходя к очередной трамвайной остановке, он не видит трамвая, то идет пешком вдоль трамвайной линии. Если в какой-то момент Петя видит трамвай, то он может принять решение вернуться на остановку, или продолжить свое движение к следующей остановке. Петя идет со скоростью U, трамвай едет со скоростью V. Нужно найти минимальное расстояние L, которое должно просматриваться перед нулевой остановкой, чтобы он мог идти со своей скоростью в сторону дома, не опасаясь, что трамвай его обгонит между остановками.
Во входном файле находятся три числа N, U и V (N ≤ 1000, U и V – положительные вещественные), за которым будет следовать N вещественных чисел – X1, X2,... Xn (0 < X1 < X2 < … < Xn < 106), разделенных пробелами.
В выходной файл ваша программа должна вывести число L с точностью до 10-4.
1 1 10 2
9.0000