Совсем недавно появилась в продаже новая компьютерная игра «Морской бой—3». Вася купил себе эту игру и теперь играет в нее в свободное от занятий время. Особенно ему нравится в одной из миссий управлять самолетом. Изначально самолет находится на палубе неподвижного авианосца и готов в любой момент к взлету. Задача игрока в этой миссии состоит в уничтожении \(N\) кораблей противника. После уничтожения всех кораблей самолет должен вернуться обратно на авианосец.

Для простоты будем считать плоской поверхность моря, где располагается авианосец. Введем прямоугольную декартову систему координат и разместим авианосец в начале координат. Каждый из кораблей в начальный момент игры находится в некоторой точке (\(x\), \(y\)), и сразу после начала игры движется равномерно и прямолинейно так, что его вектор скорости равен (\(V_x\), \(V_y\)).

Конструктивные особенности самолета таковы, что он может двигаться с любой скоростью, не превосходящей \(U\). Для того, чтобы сбросить бомбу, которая была специально придумана для этой игры, самолету необходимо находиться непосредственно над кораблем. Корабли считаются точками, т.е. размером кораблей можно пренебречь. Считается также, что самолет может мгновенно взлететь с палубы авианосца, и время падения бомбы на цель равно нулю.

Требуется написать программу, определяющую минимальное время, за которое игрок сможет уничтожить все корабли и возвратить самолет обратно на авианосец.

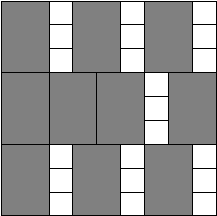
На клетчатом поле \(N\times N\), некоторые клетки которого закрашены, требуется найти размер максимального квадрата, состоящего из закрашенных клеток.

Когда Петя учился в школе, он часто участвовал в олимпиадах по информатике, математике и физике. Так как он был достаточно способным мальчиком и усердно учился, то на многих из этих олимпиад он получал дипломы. К окончанию школы у него накопилось \(n\) дипломов, причём, как оказалось, все они имели одинаковые размеры: \(w\) — в ширину и \(h\) — в высоту. Сейчас Петя учится в одном из лучших российских университетов и живёт в общежитии со своими одногруппниками. Он решил украсить свою комнату, повесив на одну из стен свои дипломы за школьные олимпиады. Так как к бетонной стене прикрепить дипломы достаточно трудно, то он решил купить специальную доску из пробкового дерева, чтобы прикрепить её к стене, а к ней — дипломы. Для того чтобы эта конструкция выглядела более красиво, Петя хочет, чтобы доска была квадратной и занимала как можно меньше места на стене. Каждый диплом должен быть размещён строго в прямоугольнике размером \(w\) на \(h\). Дипломы запрещается поворачивать на 90 градусов. Прямоугольники, соответствующие различным дипломам, не должны иметь общих внутренних точек. Требуется написать программу, которая вычислит минимальный размер стороны доски, которая потребуется Пете для размещения всех своих дипломов.

К очередной Летней компьютерной школе было решено подготовить кружки как для школьников, так и для всех преподавателей.

Имея привычку делать важные дела в самый последний момент, дизайнер закончил работу над макетом за два дня до начала школы. Ещё день уйдёт у завода-изготовителя на то, чтобы изготовить кружки и нанести на них изображение. На то, чтобы довезти кружки от завода-изготовителя до ЛКШ, остаётся всего 24 часа.

Заказ на 10000000 экземпляров кружек (а именно столько заказали организаторы), конечно же, за один рейс не увезти. Однако, за первый рейс хочется привезти максимальное количество кружек. Для перевозки был заказан один большегрузный автомобиль. Но есть один нюанс: на некоторых дорогах установлено ограничение на вес автомобиля. Поэтому если автомобиль нагрузить кружками под завязку, то, возможно, не удастся воспользоваться самым коротким маршрутом, а придётся ехать в объезд. Может случиться даже так, что из-за этого грузовик не успеет доехать до лагеря вовремя, а этого допустить никак нельзя. Итак, сколько же кружек можно погрузить в автомобиль, чтобы успеть привезти этот ценный груз вовремя, и не нарушая правил дорожного движения?