Страница: << 1 2 Отображать по:

#112547

НЛО2

Темы: [Список]

Служба безопасности Земли хочет уничтожить корабль враждебно настроенных инопланетян. Служба безопасности уже повредила корабль и заставила его сесть в пустыне. Корабль построен из кубических отсеков единичного размера и нижний слой имеет форму прямоугольника размером N × M . На рисунке показан пример вида сверху на корабль размером N = 4 , M = 8 .

$\text{[math]}$ $\text{[math]}$

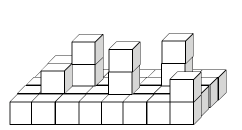
Отсеки корабля сделаны из сверхпрочного металла, поэтому для разрушения корабля используются лазеры. Лазерные установки были развернуты напротив четырех боковых сторон корабля, и они периодически выпускают лучи, перпендикулярные сторонам корабля, в сторону различных отсеков корабля. Каждый луч разрушает R первых отсеков, встретившихся на его пути. Если над уничтоженным отсеком находятся другие отсеки, то они сдвигаются вниз. Так же лазеры могут стрелять только по нижним бокам.

После K выстрелов было решено нанести по кораблю авиаудар. Для удара имеет смысл выбрать такой участок размером P × P , который целиком содержит максимальное количество уцелевших отсеков, чтобы уничтожить их все.

Напишите программу, которая вычислит, какое количество целых блоков сможет уничтожить авиаудар, нанесенный на участке размером P × P .

Входные данные

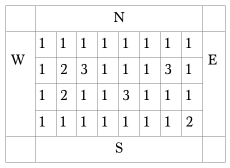
В первой строке входного файла даны 5 целых чисел: N , M ( 1 ≤ N · M ≤ 1 000 000 ), R ( 0 < R ≤ 10 ), K ( 0 < K ≤ 300 000 ) и P ( 0 < P ≤ min ( N , M , 10) ). В каждой из следующих N строк записаны по M чисел. Число в i -ой строке и j -ом столбце описывает количество единичных блоков в соответствующей части корабля аналогично рисунку. Каждое число находится в диапазоне 1..10 ⁶ .

В следующих K строках описаны выстрелы из лазеров. Каждая из этих строк содержит один символ и через пробел от него число. Символы определяют сторону воздействия: "W" — запад, "E" — восток, "S" — юг, "N" — север. Число определяет номер строки в случае запада и востока или столбца в случае севера и юга. Строки и столбцы соответствуют нумерации из входных данных, слои нумеруются с единицы. Каждое число находится в диапазоне 1..10 ⁶ .

Выходные данные

Выведите максимальное количество уцелевших отсеков после K выстрелов лазерами на участке размером P × P .

Примечание

Примеры

Входные данные

4 8 2 6 2
1 1 1 1 1 1 1 1
1 2 3 1 1 1 3 1
1 2 1 1 3 1 1 1
1 1 1 1 1 1 1 2
N 2
W 2
W 2
E 2
S 4
S 7

Выходные данные

#113941

Слабое звено

Темы: [Задачи на моделирование] [Список]

В Берляндии по воскресеньям проходит известое шоу — игра «Слабое звено».

В игре принимают участие $n$ игроков, которые выстраиваются в круг. Каждому игроку сопоставлен рейтинг — некоторое целое число $a_i$.

Игра проходит в несколько раундов, каждый из которых выглядит следующим образом:

В очередном раунде принимают участие все ещё не выбывшие игроки.
Все игроки, которые по рейтингу строго слабее обоих своих соседей по кругу, объявляются слабым звеном и выбывают из игры.
Все оставшиеся участники сдвигаются чуть плотнее, чтобы снова образовывать круг.
Игра заканчивается, если после очередного раунда осталось ровно два человека или если после очередного раунда не выбыл ни один человек.
Иначе начинается новый раунд.

Можно показать, что если до очередного раунда в игре оставалось хотя бы три участника, то после одного раунда гарантированно останется не менее двух участников.

Вам нужно выяснить для каждого участника, останется ли он до конца, или номер раунда, в котором он покинет игру.

Входные данные

В первой строке дано одно целое число $n$ ($2 \le n \le 200\,000$) — количество участников в игре.

Вторая строка содержит $n$ целых чисел $a_i$ ($1 \le a_i \le 200\,000$) — рейтинги всех участников игры в том порядке, в котором они стоят, при этом участник с номером $n$ является соседом участника с номером $1$.

Выходные данные

Выведите $n$ целых чисел — номер раунда, в котором участник игры с номером $i$ покинет игру, или $0$, если этот игрок останется до конца игры.

Раунды нумеруются последовательными целыми числами начиная с $1$.

Примечание

В первом примере игра проходит следующим образом (при помощи _ обозначаются выбывшие участники):

$[4; 5; 5; 2; 3] \to [4; 5; 5; \_; 3] \to [4; 5; 5; \_; \_] \to [\_; 5; 5; \_; \_]$

После этого игра заканчивается, так как осталось ровно два человека.

Во втором примере игра проходит следующим образом:

$[5; 1; 3; 1; 5] \to [5; \_; 3; \_; 5] \to [5; \_; \_; \_; 5]$

В третьем и чётвертом примере нет ни одного игрока, который был бы одновременно слабее обоих своих соседей, поэтому игра заканчивается, не успев начаться.

Примеры

Входные данные

5
4 5 5 2 3

Выходные данные

3 0 0 1 2

Входные данные

5
5 1 3 1 5

Выходные данные

0 1 2 1 0

Входные данные

3
6 6 6

Выходные данные

0 0 0

Входные данные

4
6 5 5 6

Выходные данные

0 0 0 0

Страница: << 1 2 Отображать по:

Выбрано

Отменить

Добавить в контест