Рассмотрим две строки \(α\) и \(β\). Их конкатенацией называется строка, получающаяся в результате приписывания к строке \(α\) строки \(β\). Эта строка обозначается \(αβ\). Например, конкатенацией строк `ab' и `ac' будет строка `abac'. Очевидно, что это определение естественным образом распространяется на конкатенацию произвольного количества строк. Так, конкатенацией нуля строк будет пустая строка, а конкатенацией одной строки будет она сама.

Рассмотрим некоторое множество \(W\), состоящее из строк. Назовём его замыканием множество \(W\)*, состоящее из тех и только тех строк, которые можно получить в результате конкатенации нуля и более строк из множества \(W\). Таким образом, множество \(W\)* содержит пустую строку, и если строка α принадлежит множеству \(W\)*, а строка \(β\) принадлежит множеству \(W\), то строка \(αβ\) принадлежит множеству \(W\)*. Более того, все элементы множества \(W\)* можно представить в таком виде, то есть \(W\)* является пересечением всех множеств с указанными выше свойствами. Например, если \(W\)={a,ab}, то \(W\)* состоит из всех строк, в которых перед каждой буквой `b' идёт хотя бы одна буква `a'.

Задано некоторое множество строк \(W\). Требуется найти множество \(X\), такое, что \(W\)*=\(X\)* и множество \(X\) имеет минимальное возможное число элементов. В случае, если таких множеств несколько, подходит любое из них. Например, если \(W\)={a,aabb,ab,ac,b,bac}, то единственным множеством, удовлетворяющим условиям задачи будет множество {a,ac,b}.

Вася любит решать головоломки со спичками. Чаще всего они формулируется следующим образом: дано изображение \(A\), составленное из спичек; переложите в нем минимальное количество спичек так, чтобы получилось изображение \(B\).

Например, из номера текущего командного чемпионата школьников Санкт-Петербурга по программированию, можно получить ромб с диагональю, переложив всего три спички.

Головоломки, которые решает Вася, всегда имеют решение. Это значит, что набор спичек, используемый в изображении \(A\), совпадает с набором спичек, используемым в изображении \(B\). Кроме того, в одном изображении никогда не встречаются две спички, у которых есть общий участок ненулевой длины (то есть спички могут пересекаться, но не могут накладываться друг на друга).

Вася устал решать головоломки вручную, и теперь он просит вас написать, программу, которая будет решать головоломки за него. Программа будет получать описания изображений \(A\) и \(B\) и должна найти минимальное количество спичек, которые надо переложить в изображении \(A\), чтобы полученная картинка получалась из \(B\) параллельным переносом.

К 50-летию первого пилотируемого полета в космос решено создать новый тип космического корабля многоразового использования “Восторг”. Прямоугольная часть его корпуса (далее прямоугольник) должна быть облицована квадратными термозащитными плитками разных цветов одного и того же размера. Прямоугольник состоит из \(r\) рядов по \(c\) плиток в каждом. Плитки должны образовывать заданный рисунок.

Облицовка космического корабля отдельными плитками очень трудоемка, поэтому для выкладывания заданного рисунка используются одинаковые прямоугольные панели, состоящие из плиток. Панели крепятся на корпусе одна за другой, заполняя ряд за рядом сверху вниз. Каждый ряд панелей может быть сдвинут относительно предыдущего на одно и то же число плиток. При этом панели могут выходить за пределы прямоугольника. Панели должны быть одинаково ориентированы, то есть при параллельном переносе одной панели на место другой цвета образующих эти панели плиток должны совпадать.

Главный конструктор хочет выбрать такой размер панели \(a\times b\) и сдвиг \(s\), чтобы этими панелями можно было выложить заданный рисунок, и площадь панели была минимальна.

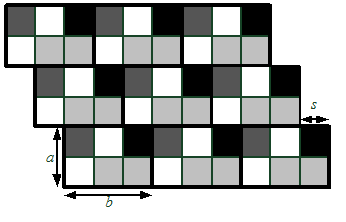
Пример панелей с \(a = 2\), \(b = 3\), \(s = 1\).

Требуется написать программу, которая по заданному расположению плиток в прямоугольнике рассчитывает размеры минимальной по площади панели, которую можно использовать при его облицовке, а также величину сдвига вправо (\(0 \leq s < b\)) каждого следующего ряда относительно предыдущего.

Комментарий

Во втором примере облицовка прямоугольника соответствуют следующему рисунку (выступающие за границы прямоугольника части панелей не показаны):