В одной маленькой стране разрешили открывать оффшорные компании, и туда тут же потянулись предприниматели с желанием открыть в ней свою фирму.
Поскольку все фирмы современные и идут в ногу со временем, им нужно связываться с клиентами и партнерами по бизнесу, а значит нужен и телефонный номер.
Таким образом, каждой букве соответствует некая цифра, и вместо телефонного номера достаточно знать слово, буквы которого соответствуют цифрам номера.
Каждая фирма хочет, чтобы ее телефонный номер было просто запомнить. Если набранное на телефоне название компании соответствует телефонному номеру компании, то номер очень легко запомнить, и ни один клиент его не забудет.
Поскольку фирм очень много, возможно, не все фирмы смогут получить удобный номер. Напишите программу, которая будет определять наибольшее количество фирм, которые смогут получить такой номер.
В первой строке вводится целое число N — количество новых фирм (1 ≤ N ≤ 103).
В последующих N строках вводятся названия фирм. Название каждой фирмы состоит из семи строчных латинских букв. Гарантируется, что названия всех фирм различны.
Выведите одно число — максимальное количество фирм, которые смогут получить удобный номер.
4 lacoste hyundai renault peugeot
4
3 aaaaaaa bbbbbbb ccccccc
1
Вася работает подмастерьем в известной студии. Недавно ему поручили помогать молодому, но подающему большие надежды художественному декоратору заборов и изгородей Витезславу Смолокурову. Миссия эта очень ответственная, и от ее выполнения зависит Васино будущее.
Стиль Смолокурова очень необычен, а его работы пользуются большим спросом. Процесс работы разделен на два этапа. На первом этапе Вася делает заготовку — длинный забор, который состоит из набора цветных вертикальных планок. На втором этапе Витезслав приступает к работе.
Для того, чтобы придать забору более спокойный и гармоничный вид, он несколько раз производит следующую операцию: выбирает некоторый цвет и отрезок, после чего перекрашивает этот отрезок забора в выбранный цвет. По своей творческой натуре, Смолокуров может в корне менять концепцию узора по нескольку раз за час, поэтому иногда он перекрашивает одну и ту же планку несколько раз. Кроме того, Витезслав не хочет, чтобы какой-то узор повторялся слишком часто. Для того, чтобы избежать этого, он иногда проверяет, не совпадает ли один отрезок забора с другим.
Несложно догадаться, что и перекрашивание, и проверки осуществляет Вася. Работа эта не самая простая, поэтому Вася просит ему помочь хотя бы с проверками на совпадение.
Первая строка входного файла содержит одно целое число n — количество планок в заборе (1 ≤ n ≤ 100 000). Вторая строка содержит n целых чисел, разделенных пробелами — цвета соответствующих планок.
Третья строка входного файла содержит одно целое число m — количество сравнений и перекрашиваний (1 ≤ m ≤ 100 000). Следующие m строк содержат описания заданий, который Вася получает от Витезслава: четыре целых числа q, l, r и k.
В случае перекрашивания q = 0. Эта запись означает перекрашивание всех планок с l по r включительно в цвет k (1 ≤ l ≤ r ≤ n). В запросе на сравнение q = 1. Эта запись означает сравнение кусков забора длины k начиная с позиций l и r соответственно (1 ≤ l, r ≤ n - k + 1, k > 0).
Все числа во входном файле положительные и не превышают 100 000.
Выведите одну строку: для каждого запроса на сравнение выведите ‘+’ в случае совпадения соответствующих кусков забора и ‘-’ в противном случае.
7 1 2 1 3 1 2 1 3 0 4 5 2 1 3 1 2 1 3 1 3
+-
2 1 2 5 1 1 2 1 0 2 2 1 1 1 2 1 0 1 2 3 1 1 1 2
-++
Ежегодно в Санкт-Петербурге, Барнауле и некоторых городах ближнего зарубежья проходят соревнования по программированию. Эти соревнования проходят в рамках студенческого чемпионата мира по программированию, организованного одной из самых авторитетных ассоциаций АСМ (Association for Computing Machinery). На этих соревнованиях проходит отбор команд с Северо-Восточного Европейского Региона NЕЕRС (North-Eastern European Regional Contest). Ежегодно перед организаторами соревнований встает проблема определения команд, которые будут приглашены к участию в финале чемпионата мира по программированию. По новым правилам в финал проходят не более N команд, представляющих NEERC. Кроме этого, от одного вуза не может проходить более чем k команд. При этот из всех таких множеств выбирается то, в котором сумма мест занятых этими командами в полуфинальных соревнованиях минимальная возможная. Ваша задача по итоговому протоколу полуфинальных соревнований и числам N и k определить, какие команды будут приглашены к участию в финале чемпионата мира.
В первой сроке входного файла находится три натуральных числа Р (1 ≤ P ≤ 100000) — количество команд, принявших участие в полуфинале, N (1 ≤ N ≤ P ) и k (1 ≤ k ≤ P ) . В следующих P строках, по одному в строке перечислены названия университетов, команды которых заняли соответствующие места. Название университета содержит строчные и прописные латинские буквы и пробелы. Длина названия университета не превышает 30 символов. В следующей строке перечислены номера команд соответствующих университетов. Таким образам если название университета записано в i -той строке (2 ≤ i ≤ P + 1) , то эта команда заняла i - 1 место на полуфинале и имеет номер, записанный на i - 1 месте в P + 2 строке.
В выходной файл выведите названия команд, приглашенных к участию в финале чемпионата мира по программированию, упорядоченных по месту, занятому на полуфинале. В качестве названия команды выведите название университета и через пробел #номер команды.
9 5 2 Fantasy University Crazy University Fantasy University Fantasy University Very Good U Good U Very Good U Crazy University Good U 1 1 2 3 2 1 1 2 2
Fantasy University #1 Crazy University #1 Fantasy University #2 Very Good U #2 Good U #1
Привидение Петя любит играть со своими кубиками. Он любит выкладывать их в ряд и разглядывать свое творение. Однако недавно друзья решили подшутить над Петей и поставили в его игровой комнате зеркало. Ведь всем известно, что привидения не отражаются в зеркале! А кубики отражаются. Теперь Петя видит перед собой N цветных кубиков, но не знает, какие из этих кубиков настоящие, а какие — всего лишь отражение в зеркале. Помогите Пете! Выясните, сколько кубиков может быть у Пети. Петя видит отражение всех кубиков в зеркале и часть кубиков, которая находится перед ним. Часть кубиков может быть позади Пети, их он не видит.
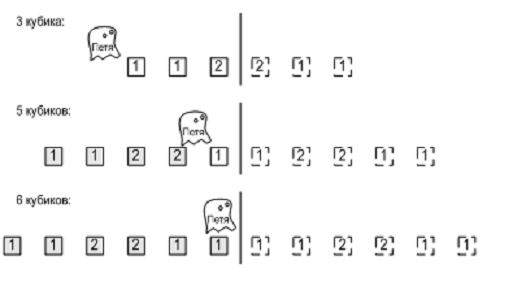
Первая строка входного файла содержит число N ( 1 ≤ N ≤ 1000000 ) и количество различных цветов, в которые могут быть раскрашены кубики — M ( 1 ≤ M ≤ 1000000 ). Следующая строка содержит N целых чисел от 1 до M — цвета кубиков.
Выведите в выходной файл все такие K , что у Пети может быть K кубиков
6 2 1 1 2 2 1 1
3 5 6
Мальчик Кирилл написал однажды на листе бумаги строчку, состоящую из больших и маленьких латинских букв, а после этого ушел играть в футбол. Когда он вернулся, то обнаружил, что его друг Дима написал под его строкой еще одну строчку такой же длины. Дима утверждает, что свою строчку он получил циклическим сдвигом строки Кирилла направо на несколько шагов(циклический сдвиг строки abcde на 2 позиции направо даст строку deabc). Однако Дима известен тем, что может случайно ошибиться в большом количестве вычислений, поэтому Кирилл в растерянности – верить ли Диме? Помогите ему!
По данным строкам выведите минимальный возможный размер сдвига или –1, если Дима ошибся.
Первые две строки входного файла содержат строки Кирилла и Димы соответственно. Длины строк одинаковы, не превышают 100000 и не равны 0.
В выходной файл выведите единственное число – ответ на поставленную задачу
a b
-1
zabcd abcdz
4