Однажды в далекой-далекой стране правительство создало Министерство по сокращению бумажной волокиты. Как вы наверное догадались, это было крупнейшее министерство за всю историю страны. Количество сотрудников было поистине огромным. Несмотря на это, структура министерства была очень простой: каждый сотрудник имел не более трёх подчинённых, каждый из которых снова имел не более трех подчиненных и так далее...
В результате последних выборов был избран новый министр. Он был молод, умён и непорочен, и сразу же решил оправдать название своего учреждения. Он заметил, что многие части иерархической структуры совпадают, и решил, что должны совпадать и их обязанности. А если две структуры делают одно и тоже, одна из них является лишней, и ее работники должны быть уволены. Ваша задача найти количество различных департаментов и вывести результат в необходимом формате.
Вам дана структура министерства. Каждый работник имеет одного начальника и не более трёх подчинённых(возможно ноль). Единственным исключением является министр — у него нет начальника(но так же не более трех подчинённых). Конечно нет определённого порядка, в котором перечисляются подчинённые. Департамент состоит из должностного лица, всех его подчинённых и их подчинённых, и т.д.
Есть два особых случая:
-
Департамент, в котором должностное лицо — сам министр, тогда этот департамент есть всё министерство.
- Департамент, в котором у должностного лица нет ни одного подчинённого.
Высотой департамента назовем длину максимальной последовательность сотрудников x 1 , ..., x d такую, что сотрудник x i является начальником сотрудника x i + 1 для всех 1 ≤ i < d . Заметим что высота департамента, состоящего из одного сотрудника равна 1 .
Два департамента A и B совпадают, если существует взаимно-однозначное отображение, сопоставляющее каждому сотруднику x A из департамента A сотрудника x B из департамента B , таким образом, что сотрудник x A является начальником сотрудником y A , тогда и только тогда, когда x B является начальником y B . Заметим, что если два департамента совпадают, то они имеют одинаковую высоту, одинаковое количество сотрудников и начальнику первого департамента соответствует начальник второго.
На приведенных картинках департаменты A и B совпадают, а C не совпадает ни с A , ни c B .
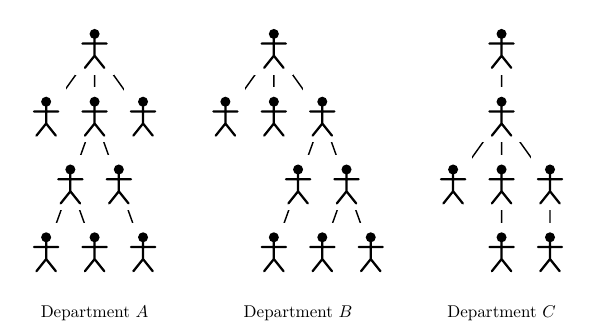
Вам необходимо для каждой высоты вычислить количество различных департаментов имеющих такую глубину. Формально требуется построить последовательность n 1 , ..., n d , где d это высота всего министерства, а n i — количество различных департаментов высоты i .
Входной файл содержит единственную строку, которая описывает иерархическую структуру министерства, используя следующую нотацию. Каждый департамент кодируются строкой "( x 1 ... x k )", где k — количество подчинённых у начальника департамента, а строки x i — коды им подчиняющихся департаментов. Департамент, состоящий из одного человека, кодируется строкой "()". Структура министерства задается кодом всего министерства. Количество сотрудников министерства не превосходит 1 000 000 (включая министра).
Выходной файл должен содержать d строк, где d это высота министерства. i -ая строка должна содержать количество различных департаментов высоты i .
Приведенная картинка иллюстрирует пример из условия.
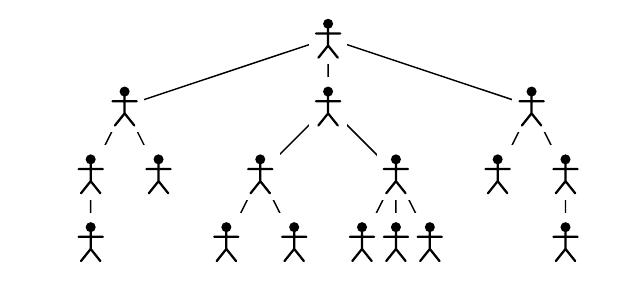
(((())())((()())(()()()))(()(())))
1 3 2 1
Известно, что в солнечной системе есть 8 планет и один планетоид. Мало кто знает, что ещё есть секретная планета, населенная медведями. Именно туда ассоциация Savez отправляет бравого генерала Хенрика для изучения медведей. Выяснилось, что медведи умеют телепортироваться. Расчётливый генерал Хедрик решил завербовать их в свою армию.
У одного медведя есть N строк (обозначим i -ю из них x i ). Исследования показывают, что количество раз, которое может телепортироваться медведь равно длине наибольшей подпоследовательности этих строк, удовлетворяющей такому правилу: строки x i и x j ( i < j ) могут принадлежать одной такой последовательности, если x i является и префиксом, и суффиксом x j .
Помогите уставшему от долгого полёта генералу Хендрику определить, сколько телепортаций сможет сделать данный медведь.
В первой строке содержится одно целое число N – количество строк, которые есть у медведя. В последующих N строках содержатся сами эти строки. Входной файл содержит не более двух миллионов символов.
Выведите одно число – ответ на вопрос любопытного генерала Хендрика.
В первом примере наибольшая последовательность A -> AA -> AAA В третьем примере наибольшая последовательность A -> A -> A или B -> B -> B
5 A B AA BBB AAA
3
5 A ABA BBB ABABA AAAAAB
3
6 A B A B A B
3
У маленького Матежа возникла проблема с решением следующей задачи.
У него есть множество слов, содержащее N слов. Ему пришло Q запросов, являющихся шаблонами. Шаблон состоит из строчных латинских букв и символа '*'.
Требуется узнать, сколько слов из множества могут совпасть с шаблоном, если вместо '*' подставить любое (возможно, пустое) множество букв.
В первой строке содержатся N и Q ( 1 ≤ N , Q ≤ 10 5 ). В последующих N строках содержатся строки из множества. В последующих Q строках содержатся шаблоны. Входной файл содержит не более трех миллионов символов.
Выведите Q строк: в каждой ответ для соответствующего шаблона.
40 баллов: 1 ≤ N , Q ≤ 1000
3 3 aaa abc aba a*a aaa* *aaa
2 1 1
5 3 eedecc ebdecb eaba ebcddc eb e* *dca e*c
5 0 2
Вам дан массив целых чисел длины N . Пусть s 1 , s 2 , ... , s q - массив его непустых подпоследовательностей, отсортированный в лексикографическом порядке.
Подпоследовательностью массива называется массив, полученным путем вычеркивания нескольких (возможно, 0) элементов из изначального массива. Заметьте, что некоторые подпоследовательности могут быть одинаковыми, поэтому q = 2 N - 1 .
Массив A лексикографически меньше массива B , если A i < B i , где i - первая позиция, в которой массивы различаются, или если A - строгий префикс B .
Определим хеш массива s , состоящего из элементов v 1 , v 2 , ... , v p , как: h ( s ) = ( v 1 · B p - 1 + v 2 · B p - 2 + ... + v p - 1 · B + v p ) mod M , где B и M - данные числа.
Посчитайте h ( s 1 ) , h ( s 2 ) , ... , h ( s K ) для данного K .
В первой строке содержатся числа N , K , B , M ( 1 ≤ N ≤ 100000 , 1 ≤ K ≤ 100000 , 1 ≤ B , M ≤ 1000000 ).
Во второй строке содержится N чисел a 1 , a 2 , a 3 , ... , a N ( 1 ≤ a i ≤ 100000 ).
Гарантируется, что во всех тестах K ≤ 2 N - 1 .
Выведите K строк, j -я строка должна содержать h ( s j ) и длину s j .
Решения, работающие при 1 ≤ a 1 , a 2 , ..., a N ≤ 30 , будут оцениваться в 60 баллов.
2 3 1 5 1 2
1 1 3 2 2 1
3 4 2 3 1 3 1
1 1 1 1 0 2 2 2
5 6 23 1000 1 2 4 2 3
1 1 25 2 25 2 577 3 274 4 578 3
Палиндром - это слово, которое читается справа налево также, как слева направо. Например, "a", "abba", "anavolimilovana" - палиндромы.
Весом строки, состоящей из строчных латинских символов будем называть количество ее подстрок (слов), являющихся палиндромами (при этом каждое вхождение подстроки считается отдельно). Формально, пусть W - строка длины N . Слово w a , b - подстрока W , состоящая из символов на позициях с индексами с a по b включительно. Вес строки W - это количество пар целых чисел a , b ( 1 ≤ a , b ≤ N ) таких, что w a , b является палиндромом.
Вам дана строка, состоящая из строчных латинских символов. Вы можете либо оставить ее неизменной, либо поменять любой из ее символов на любой другой символ. Найдите максимально возможный вес строки, которую вы можете получить.
Первая строка содержит одну строку W ( 1 ≤ | W | ≤ 100000 ), состоящую из строчных латинских символов.
Выведите одно целое число - максимально возможный вес.
Решения, работающие при
|
W
| ≤ 100
, будут оцениваться в 17 баллов.
Решения, работающие при
|
W
| ≤ 5000
, будут оцениваться еще в 37 баллов.
aaaa
10
baccb
9
slavko
7