Крешо купил вкуснейший сыр с перцем, но Степану перец не нравится, поэтому он хочет отрезать кусок, на котором не было бы перца. Сыр имеет форму выпуклого многоугольника, а каждая перчинка является точкой внутри него. Степан режет сыр только 1 раз. Он выбирает две вершины многоугольника, не являющиеся смежными, и режет по диагонали, соединяющей их. Затем Степан забирает ту из получившихся частей, на которой нет перца (ни внутри, ни на границе).

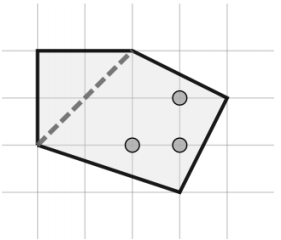
Рисунок соответствует первому тесту. Пунктирной линией показан разрез Степана.

Напишите программу, которая определит, может ли Степан отрезать кусок без перца. Если он может это сделать, выведите максимальную площадь куска, который может отрезать Степан.

Рассмотрим строку \(s\), состоящую из строчных букв латинского алфавита. Примером такой строки является, например, строка «abba».

Подстрокой строки \(s\) называется строка, составленная из одного или нескольких подряд идущих символов строки \(s\). Обозначим как \(W(s)\) множество, состоящее из всех возможных подстрок строки \(s\). При этом каждая подстрока входит в это множество не более одного раза, даже если она встречается в строке \(s\) несколько раз.

Например, \(W\)(«abba») = {«a», «b», «ab», «ba», «bb», «abb», «bba», «abba»}.

Подпоследовательностью строки \(s\) называется строка, которую можно получить из \(s\) удалением произвольного числа символов. Обозначим как \(Y\)(\(s\)) множество, состоящее из всех возможных подпоследовательностей строки \(s\). Аналогично \(W\)(\(s\)), каждая подпоследовательность строки \(s\) включается в \(Y\)(\(s\)) ровно один раз, даже если она может быть получена несколькими способами удаления символов из строки \(s\). Поскольку любая подстрока строки \(s\) является также ее подпоследовательностью, то множество \(Y\)(\(s\)) включает в себя \(W\)(\(s\)), но может содержать также и другие строки.

Например, \(Y\)(«abba») = \(W\)(«abba») ∪ {«aa», «aba»}. Знак ∪ обозначает объединение множеств.

Будем называть строку \(s\) странной, если для нее \(W\)(\(s\)) = \(Y\)(\(s\)). Так, строка «abba» не является странной, а, например, строка «abb» является, так как для нее \(W\)(«abb») = \(Y\)(«abb») = {«a», «b», «ab», «bb», «abb»}.

Будем называть странностью строки число ее различных странных подстрок. При вычислении странности подстрока считается один раз, даже если она встречается в строке \(s\) в качестве подстроки несколько раз. Так, для строки «abba» ее странность равна 7, любая ее подстрока, кроме всей строки, является странной.

Требуется написать программу, которая по заданной строке \(s\) определяет ее странность.

Знаменитый художник Вася только что закончил работу над своим новым шедевром и хочет знать, сколько он сможет получить за свой труд.

Картина представляет собой прямоугольник N на M сантиметров, разделенный на маленькие квадратики 1 на 1 сантиметр со сторонами, параллельными сторонам картины. Для достижения гармонии каждый из этих квадратиков Вася покрасил одним из 26 особых цветов, обозначаемых маленькими латинскими буквами.

Стоимость картины в точности равна количеству «симпатичных» частей в ней. Частью картины называется любой прямоугольник, который может быть вырезан из нее по границам квадратиков. Часть называется «симпатичной», если при выполнении симметрии относительно ее центра получается прямоугольник, раскрашенный также, как и исходная часть. Например, в картине, раскрашенной так:

abc
acb

симпатичными являются все части, состоящие из одного квадратика (их 6), а также части

cb и a

Напишите программу, которая по информации о шедевре Васи определит его стоимость.