Для проведения олимпиады школьников по информатике требуется соединить компьютеры в сеть. Организаторы олимпиады разработали схему соединения компьютеров. В соответствии с этой схемой некоторые пары компьютеров должны быть соединены кабелем, и сигнал сможет дойти по кабелям от любого компьютера до любого другого, возможно, через другие компьютеры.
Некоторые компьютеры могут быть соединены циклически. Цикл называется простым, если каждый компьютер из этого цикла соединён ровно с двумя другими компьютерами этого цикла, и в этот цикл никакой кабель не входит более одного раза. Некоторые кабели могут не входить ни в какой цикл.
Известно, что в разработанной схеме никакой кабель не принадлежит двум простым циклам одновременно.
Организаторам олимпиады поручено разместить компьютеры в зале соревнований. При размещении должны выполняться следующие условия:
1.Компьютеры размещаются на плоскости в точках с целочисленными координатами.
2.Координаты компьютеров x и y лежат в диапазоне 0 ≤ x, y ≤ 106.
3.Никакие два компьютера не располагаются в одной точке.
4.Кабели являются отрезками прямых.
5.Кабели не пересекаются между собой и не проходят через точки размещения компьютеров, к которым они не подключены.
Требуется написать программу, выполняющую размещение компьютеров по заданному описанию схемы.
В первой строке входного файла содержатся числа N и M — количество компьютеров и количество кабелей в схеме (1 ≤ N ≤ 100 000, 0 ≤ M ≤ 200 000). В последующих M строках содержатся пары чисел, разделенных пробелами. Каждая такая пара описывает один кабель, числа представляют собой номера соединенных компьютеров. Компьютеры пронумерованы от 1 до N. Никакая пара не встречается дважды, и никакой кабель не соединяет компьютер с самим собой.
Выходной файл должен содержать N строк. Строка с номером i должна содержать координаты i-го компьютера, разделенные пробелом. Сначала выводится координата x, затем y. Разрешается вывести любой вариант размещения компьютеров, при котором выполняются условия 1–5.
Примечания
- Подзадача 0 (0 баллов) тесты из условия.
- Подзадача 1 (10 баллов) \( n \le 10\) граф без циклов.
- Подзадача 2 (20 баллов) \( n \le 10^3\) граф без циклов. Необходимые подгруппы: 1.
- Подзадача 3 (10 баллов) \( n \le 10^5\) граф без циклов. Необходимые подгруппы: 1, 2.
- Подзадача 4 (4 баллов) \( n \le 10\) граф с одним циклом.
- Подзадача 5 (8 баллов) \( n \le 10^3\) граф с одним циклом. Необходимые подгруппы: 4.
- Подзадача 6 (8 баллов) \( n \le 10^5\) граф с одним циклом. Необходимые подгруппы: 4, 5.
- Подзадача 7 (4 баллов) \( n \le 10\) граф, в котором каждая вершина лежит не более чем на одном цикле.
- Подзадача 8 (8 баллов) \( n \le 10^3\) граф, в котором каждая вершина лежит не более чем на одном цикле. Необходимые подгруппы: 7.
- Подзадача 9 (8 баллов) \( n \le 10^5\) граф, в котором каждая вершина лежит не более чем на одном цикле. Необходимые подгруппы: 7, 8.
- Подзадача 10 (2 баллов) \( n \le 10\) граф, в котором каждое ребро лежит не более чем на одном цикле.
- Подзадача 11 (4 баллов) \( n \le 10^3\) граф, в котором каждое ребро лежит не более чем на одном цикле. Необходимые подгруппы: 10.
- Подзадача 12 (14 баллов) \( n \le 10^5\) граф, в котором каждое ребро лежит не более чем на одном цикле. Необходимые подгруппы: 10, 11.
Пример входных и выходных данных
|
Ввод |
Вывод |
|
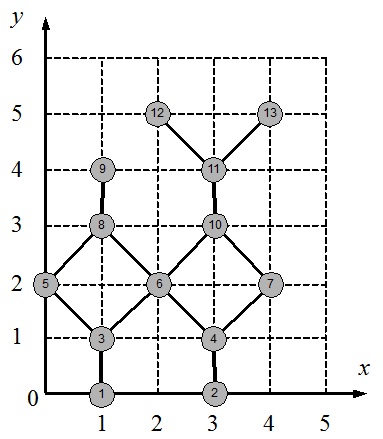
13 14 11 12 11 13 1 3 3 5 5 8 8 9 8 6 6 3 4 6 4 2 6 10 10 11 10 7 7 4 |
1 0 3 0 1 1 3 1 0 2 2 2 4 2 1 3 1 4 3 3 3 4 2 5 4 5 |
Над ареной огромного спортивного комплекса Независимого Главного Университета (НГУ) решили построить перекрытие. Перекрытие будет построено по клеевой технологии и состоять из склеенных друг с другом блоков. Блок представляет собой легкий прямоугольный параллелепипед. Два блока можно склеить, если они соприкасаются перекрывающимися частями боковых граней ненулевой площади.
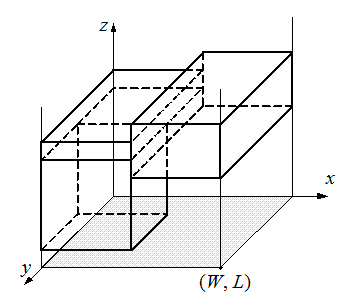
НГУ представил план комплекса, имеющий вид прямоугольника размером W на L. При этом один из углов прямоугольника находится в начале системы координат, а другой имеет координаты (W, L). Стены комплекса параллельны осям координат.
Подрядчики известили НГУ, что они готовы к определенному сроку изготовить блоки и установить их. Для каждого блока фиксировано место его возможного монтажа, совпадающее по размерам с этим блоком. Места выбраны так, что ребра блоков параллельны осям координат. Места монтажа блоков не пересекаются.
По техническим условиям перекрытие должно состоять из такого набора склеенных блоков, который содержит сплошной горизонтальный слой ненулевой толщины. Торопясь ввести комплекс в эксплуатацию, НГУ решил построить перекрытие из минимально возможного числа блоков.
Требуется написать программу, которая позволяет выбрать минимальное число блоков, которые, будучи установленными на указанных подрядчиками местах, образуют перекрытие, либо определить, что этого сделать невозможно. Высота, на которой образуется перекрытие, не имеет значения.
В первой строке входного файла указаны три целых числа: N — количество возможных блоков (1 ≤ N ≤ 105) и размеры комплекса W и L (1 ≤ W, L ≤ 104). Каждая из последующих N строк описывает место монтажа одного блока, определяемое координатами противоположных углов: (x1, y1, z1) и (x2, y2, z2), при этом 0 ≤ x1 < x2 ≤ W, 0 ≤ y1 < y2 ≤ L, 0 ≤ z1 < z2 ≤ 109. Все числа во входном файле целые и разделяются пробелами или переводами строк.
Гарантируется, что места установки блоков не пересекаются друг с другом.
Первая строка выходного файла должна содержать либо слово «YES», если перекрытие возможно построить, иначе — слово «NO». В первом случае вторая строка выходного файла должна содержать минимальное число блоков, образующих перекрытие, а последующие строки — номера этих блоков, в соответствии с порядком, в котором они перечислены во входном файле.
Если возможно несколько минимальных наборов блоков, выведите любой из них.
Примечания
Решения, корректно работающие в случае, когда все числа во входном файле не превышают 100, будут оцениваться из 40 баллов.
1 10 10 0 0 0 10 10 10
YES 1 1
2 10 10 0 0 0 10 5 5 0 5 5 10 10 10
NO
Как много открытий можно сделать, исследуя числа и составляющие их цифры!
Петя очень любит арифметику, и кроме домашних заданий он постоянно придумывает дополнительные задачи. Однажды он стал прибавлять к натуральным числам сумму составляющих их цифр. Петя обнаружил, что некоторые числа, например 20, не могут быть получены из других чисел в результате такого действия. Эти числа ему не понравились, и он назвал их некрасивыми.
Позже, когда Петя начал изучать информатику, те же исследования он стал проводить с натуральными числами в двоичной системе счисления. Например, двоичное число 11102 (в десятичной системе — 14) можно получить из числа 11002 (в десятичной системе — 12), прибавив к последнему сумму его цифр:
11002 + 102 = 11102.
Петя решил исследовать множество двоичных некрасивых чисел. Первые пять некрасивых чисел он нашел без труда: 1 = 12, 4 = 1002, 6 = 1102, 13 = 11012, 15 = 11112. Продолжить работу он собирается с помощью компьютера.
Требуется написать программу, которая определяет количество двоичных некрасивых чисел, не превосходящих заданного числа n.
В первой строке входного файла содержится число n, записанное в десятичной системе счисления (1 ≤ n ≤ 1018).
В единственной строке выходного файла должно содержаться единственное число — количество двоичных некрасивых чисел, не превосходящих n.
Примечание
Решения, корректно работающие при n ≤ 106, будут оцениваться из 40 баллов.
17
5
18
6
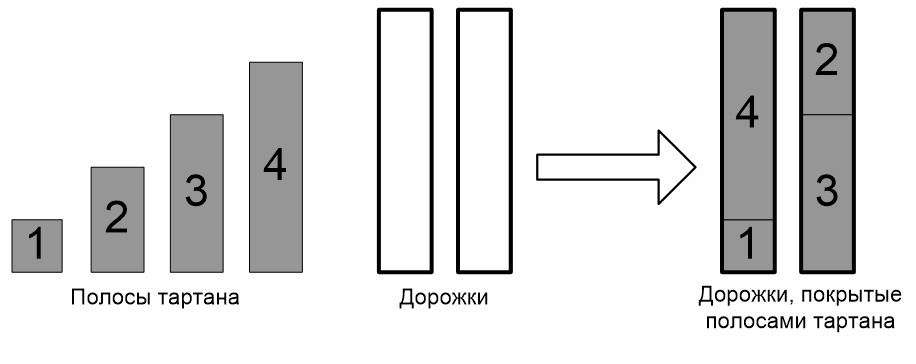
В стране Флатландия решили построить легкоатлетический манеж с M одинаковыми прямолинейными беговыми дорожками. Они будут покрыты полосами из синтетического материала пружинкин. На складе имеются N полос пружинкина, длины которых равны 1, 2, …, N метров соответственно (i-я полоса имеет длину i метров).
Было решено использовать все полосы со склада, что определило длину дорожек манежа. Полосы пружинкина должны быть уложены без перекрытий и промежутков. Разрезать полосы на части нельзя. Полосы укладываются вдоль дорожек, ширина полосы пружинкина совпадает с шириной беговой дорожки.
Требуется написать программу, которая определяет, можно ли покрыть всем имеющимся материалом M дорожек, и если это возможно, то распределяет полосы пружинкина по дорожкам.
Во входном файле содержатся два целых числа, разделенных пробелом: M — количество дорожек и N — количество полос пружинкина (1 ≤ M ≤ 1000, 1 ≤ N ≤ 30000).
В случае, если распределить имеющиеся полосы пружинкина на M дорожек одинаковой длины невозможно, то в выходной файл выведите слово «NO».
В противном случае, в первую строку выведите слово «YES». В последующих M строках дайте описание использованных полос для каждой дорожки в следующем формате: сначала целое число t — количество полос на дорожке, затем t целых чисел — длины полос, которые составят эту дорожку. Если решений несколько, можно вывести любое из них.
В задаче есть группа на первые 17 тестов и она оценивается в 20 баллов. затем идёт потестовая оценка по 2 балла за пройденный тест.
Примеры входных и выходных данных
| Ввод | Вывод |
| 2 4 | YES 2 1 4 2 3 2 |
| 3 4 | NO |
Около прямолинейного забора, состоящего из N одинаковых бетонных плит, проводится конкурс граффити, в котором участвуют M граффити-художников. Художники должны разрисовать все плиты своими произведениями за наименьшее возможное время.
Плиты пронумерованы числами от 1 до N, граффити-художники имеют номера от 1 до M. Первоначально i-й граффити-художник находится около плиты с заданным номером pi. Каждому художнику требуется b минут на разрисовывание любой плиты. Каждую плиту должен разрисовать ровно один граффити-художник.
В начале работы, а также после разрисовывания любой плиты граффити-художник может перейти к любой неразрисованной плите. Время перемещения граффити-художника от любой плиты к соседней с ней одинаково и равно a минут. Таким образом, чтобы перейти от плиты с номером i к плите с номером j художнику требуется a×|i – j| минут.
Требуется написать программу, которая поможет участникам конкурса разрисовать все плиты за минимальное возможное время.
В первой строке входного файла указаны числа N — количество плит в заборе и M — количество граффити-художников (1 ≤ N, M ≤ 100000). Во второй строке заданы два целых числа: a — количество минут, которое требуется для перехода от любой плиты к соседней, и b — количество минут, которое требуется граффити-художнику на разрисовывание одной плиты (1 ≤ a, b ≤ 106). В третьей строке заданы M чисел p1, p2, …, pM — начальные положения граффити-художников (1 ≤ pi ≤ N).
В первую строку выходного файла выведите минимальное количество минут, требуемых художникам для выполнения работы.
В последующих M строках выведите описание действий художников. В i-й из этих строк должно содержаться описание действий i-го художника: количество плит, которые должен разрисовать этот художник, и номера этих плит в очередности их разрисовывания. Если оптимальных решений несколько, можно вывести любое из них.
Примечание
Решения, корректно работающие при M ≤ 2, будут оцениваться из 40 баллов.
10 2 19 56 9 2
375 5 10 9 8 7 6 5 1 2 3 4 5