Расшифровка письменности Майя оказалась более сложной задачей, чем предполагалось ранними исследованиями. На протяжении более чем двух сотен лет удалось узнать не так уж много. Основные результаты были получены за последние 30 лет.
Письменность Майя основывается на маленьких рисунках, известных как значки, которые обозначают звуки. Слова языка Майя обычно записываются с помощью этих значков, которые располагаются рядом друг с другом в некотором порядке.
Одна из проблем расшифровки письменности Майя заключается в определении этого порядка. Рисуя значки некоторого слова, писатели Майя иногда выбирали позиции для значков, исходя скорее из эстетических взглядов, а не определенных правил. Это привело к тому, что, хотя звуки для многих значков известны, археологи не всегда уверены, как должно произноситься записанное слово.
Археологи ищут некоторое слово \(W\). Они знают значки для него, но не знают все возможные способы их расположения. Поскольку они знают, что Вы приедете на IOI ’06, они просят Вас о помощи. Они дадут Вам \(g\) значков, составляющих слово \(W\), и последовательность \(S\) всех значков в надписи, которую они изучают, в порядке их появления. Помогите им, подсчитав количество возможных появлений слова \(W\).
Напишите программу, которая по значкам слова \(W\) и по последовательности \(S\) значков надписи подсчитывает количество всех возможных вхождений слова \(W\) в \(S\), то есть количество всех различных позиций идущих подряд \(g\) значков в последовательности \(S\), которые являются какой-либо перестановкой значков слова \(W\) .
1 ≤ \(g\) ≤ 3 000, \(g\) – количество значков в слове \(W\)
\(g\) ≤ |\(S\)| ≤ 3 000 000 где |\(S\)| – количество значков в последовательности \(S\)
На вход программы поступают данные в следующем формате:
СТРОКА 1: Содержит два числа, разделенных пробелом – \(g\) и |\(S\)|.
СТРОКА 2: Содержит \(g\) последовательных символов, с помощью которых записывается слово \(W\) . Допустимы символы: ‘a’-‘z’ и ‘A’-‘Z’; большие и маленькие буквы считаются различными.
СТРОКА 3: Содержит |\(S\)| последовательных символов, которые представляют значки в надписи. Допустимы символы: ‘a’-‘z’ и ‘A’-‘Z’; большие и маленькие буквы считаются различными.
Единственная строка выходных данных программы должна содержать количество возможных вхождений слова \(W\) в \(S\).
Для части тестов, оцениваемых в 50 баллов, выполняется ограничение \(g\) ≤ 10.
По умолчанию во FreePascal переменная типа string имеет ограничение размера в 255 символов. Если Вы хотите использовать более длинные строки, Вы должны добавить директиву {$ H +} в ваш код, сразу после строки program ...;.
4 11 cAda AbrAcadAbRa
2
После победы в великой битве Король Ягуар хочет построить пирамиду, которая будет одновременно монументом в честь победы и гробницей для погибших солдат. Пирамида будет построена на поле боя. Она должна иметь прямоугольное основание, состоящее из \(a\) столбцов и \(b\) строк. Для сохранения останков и оружия павших солдат внутри основания пирамиды будет располагаться небольшая прямоугольная комната, состоящая из \(c\) столбцов и \(d\) строк.
Архитекторы Короля представили поле боя в виде прямоугольной сетки. Эта сетка состоит из квадратных клеток единичной площади и имеет \(m\) столбцов и \(n\) строк. Для каждой клетки они измерили ее высоту и получили некоторое целое число.
Основание пирамиды и комната должны покрывать включаемые ими клетки полностью, а их стороны должны быть параллельны сторонам поля боя. Высоты клеток, составляющих комнату, должны остаться неизменными, а высоты всех клеток основания пирамиды будут выровнены с помощью перемещения песка с более высоких клеток на более низкие. В результате этого высота основания пирамиды будет равна среднему арифметическому высот всех его клеток (за исключением клеток комнаты). Архитекторы могут выбрать любое местоположение для комнаты внутри пирамиды, но обязательно оставлять вокруг комнаты стену основания пирамиды толщиной хотя бы в одну клетку.
Помогите архитекторам выбрать наилучшее место для расположения пирамиды и комнаты внутри нее так, чтобы высота основания пирамиды была максимально возможной при заданных размерах.
На рисунке показан пример поля боя, где число в каждой клетке обозначает ее высоту. Клетки, составляющие основание пирамиды, обозначены серым цветом, а белые клетки внутри основания пирамиды соответствуют расположению комнаты. На этом рисунке представлен пример оптимального решения.
Напишите программу, которая по заданным размерам поля боя, пирамиды и комнаты, а также по заданным высотам всех клеток будет находить такое расположение пирамиды и комнаты внутри нее, что получившаяся высота основания пирамиды будет максимально возможной.
3 ≤ \(m\) ≤ 1000
3 ≤ \(n\) ≤ 1000
3 ≤ \(a\) ≤ \(m\)
3 ≤ \(b\) ≤ \(n\)
1 ≤ \(c\) ≤ \(a\) – 2
1 ≤ \(d\) ≤ \(b\) – 2
Все высоты – целые числа от 1 до 100.
Ваша программа получает входные данные в следующем формате:
СТРОКА 1: Содержит шесть целых чисел, разделенных пробелами, в следующем порядке: \(m\), \(n\), \(a\), \(b\), \(c\) и \(d\).
СЛЕДУЮЩИЕ \(n\) СТРОК: Каждая из этих строк содержит m целых чисел, разделенных пробелами. Эти числа соответствуют высотам клеток в одной строке сетки. Первая из этих строк соответствует верхней строке (строке 1) сетки, а последняя – нижней строке (строке \(n\)). При этом \(m\) чисел в каждой строке соответствуют высотам клеток этой строки, начиная со столбца 1.
Ваша программа должна вывести следующие данные:
СТРОКА 1: Должна содержать два целых числа, разделенные пробелом, – координаты левой верхней клетки основания пирамиды, при этом первое число соответствует столбцу, а второе – строке.
СТРОКА 2: Должна содержать два целых числа, разделенные пробелом, – координаты левой верхней клетки комнаты, при этом первое число соответствует столбцу, а второе – строке.
Если существует несколько оптимальных положений пирамиды и комнаты, выведите любое из них.
Ряд тестов с общей суммой 30 баллов будет удовлетворять следующим ограничениям:
3 ≤ \(m\) ≤ 10
3 ≤ \(n\) ≤ 10
8 5 5 3 2 1 1 5 10 3 7 1 2 5 6 12 4 4 3 3 1 5 2 4 3 1 6 6 19 8 1 1 1 3 4 2 4 5 6 6 3 3 3 2 2 2
1 4 1 6 2
Город Мехико расположен в прекрасной долине, известной как Долина Мехико, на месте которой много лет назад было озеро. Около 1300 года ацтекские религиозные лидеры выпустили указ о том, что центр озера должен быть засыпан, чтобы построить столицу их империи. В настоящее время озеро полностью осушено.
Вокруг озера до появления ацтеков были расположены c прибрежных городов. Некоторые из этих городов заключили между собой коммерческие соглашения. Между городами, установившими коммерческие соглашения, по озеру на лодках перевозились различные товары. Любую пару городов можно было соединить отрезком прямой, полностью проходящим через озеро.
В какой-то момент короли городов решили упорядочить товароперевозки. Они разработали маршрут товароперевозок, который соединяет все города вокруг озера. Маршрут удовлетворяет следующим условиям:
*Он начинается в каком-либо городе, проходит через каждый прибрежный город и заканчивается в городе, отличном от того, в котором он начался.
*Маршрут проходит через каждый город ровно один раз.
*Любые два последовательно посещаемых города маршрута обязаны иметь между собой коммерческое соглашение.
*Маршрут состоит из отрезков прямых, каждый из которых соединяет два последовательно посещаемых города маршрута.
*Чтобы избежать столкновения лодок, маршрут не должен иметь самопересечений.
Этот маршрут нигде не имеет самопересечений. Но если построить маршрут, идущий из города 2 в город 6, затем в город 5, а затем в город 1, то он будет неправильным, поскольку имеет самопересечения.
Города нумеруются целыми числами от 1 до \(c\) по направлению часовой стрелки.
Напишите программу, которая по заданному числу городов \(c\) и списку коммерческих соглашений между городами, найдет маршрут товароперевозок, удовлетворяющий указанным выше условиям.
3 ≤ \(c\) ≤ 1000, \(c\) – число городов вокруг озера
На вход Вашей программы поступают данные в следующем формате:
СТРОКА 1: Содержит целое число \(c\).
СТРОКА 2: Содержит целое число \(n\) – количество коммерческих соглашений.
СЛЕДУЮЩИЕ \(n\) СТРОК: Каждая строка описывает одно коммерческое соглашение (одно соглашение описывается один раз). В строке задаются два целых числа, разделенных пробелами, которые соответствуют номерам городов, заключивших между собой коммерческое соглашение.
Если возможно построить маршрут товароперевозок, выведите c строк, в каждой из которых записано целое число. Эти числа представляют собой порядок посещения городов по маршруту товароперевозок. Если невозможно построить маршрут товароперевозок, удовлетворяющий всем указанным требованиям, выведите одну строку, содержащую отрицательное целое число -1.
Если существует несколько маршрутов товароперевозок, удовлетворяющих всем указанным требованиям, выведите любой из них.
Ряд тестов с общей суммой 30 баллов будет удовлетворять следующим ограничениям:
3 ≤ \(m\) ≤ 10
3 ≤ \(n\) ≤ 10
7 9 1 4 5 1 1 7 5 6 2 3 3 4 2 6 4 6 6 7
5 6 7 1 4 3 2
«Соединение точек» – это игра для одного игрока. Игровое поле строится следующим образом. Выбираются два целых числа, каждое из которых больше 2, которые обозначаются \(g\) и \(r\). Затем на плоскости рисуются четыре точки в вершинах квадрата, две верхние
из них становятся зелеными точками, а две нижние – красными. Далее внутри квадрата рисуются зеленые и красные точки таким образом, что никакие три точки, включая вершины квадрата, не лежат на одной прямой. Процесс продолжается до тех пор,
пока общее количество зеленых точек не станет равным \(g\), а количество красных точек – равным \(r\).
После того, как игровое поле нарисовано, игрок начинает соединять точки. Две точки можно соединять отрезком, соблюдая следующие условия:
*соединяются только две точки одного цвета;
*отрезок, соединяющий точки, не пересекает никакой из ранее нарисованных отрезков (кроме как по концам отрезков).
Будем считать, что две точки \(u\) и \(v\) принадлежат одной компоненте,
если от \(u\) до \(v\) можно дойти по нарисованным отрезкам.
Цель игры – соединить все зеленые точки в одну компоненту с помощью (\(g\) – 1) отрезков, а все красные точки – в другую компоненту с помощью (\(r\) – 1) отрезков. Можно доказать, что при вышеописанном способе расположения точек всегда существует способ выиграть игру.
Вам будет задано квадратное игровое поле со стороной \(s\), а также \(g\) зелеными и \(r\) красными точками. Координаты точек задаются парами целых чисел (\(x_i\), \(y_i\)). Зеленые точки пронумерованы числами от 1 до \(g\) так, что верхняя
левая точка (0, \(s\)) имеет номер 1, верхняя правая точка (\(s\), \(s\)) – номер 2, а остальные точки – номера от 3 до \(g\) (в произвольном порядке). Красные точки пронумерованы числами от 1 до \(r\) так, что нижняя левая точка (0, 0) имеет
номер 1, нижняя правая точка (\(s\), 0) – номер 2, а остальные точки – номера от 3 до \(r\) (в произвольном порядке).
Легко видеть, что никакие три точки на рисунке не лежат на одной прямой, и никакие два отрезка не пересекаются, кроме как по концам.
Напишите программу, которая по заданным координатам g зеленых точек и координатам \(r\) красных точек находит способ, как нарисовать (\(g\) – 1) зеленых отрезков и (\(r\) – 1) красных отрезков таким образом, чтобы все зеленые точки принадлежали одной компоненте, а все красные точки – другой, и никакие два отрезка не пересекались.
\(3 \le g \le 50 000, g\) – количество зеленых точек
\(3 \le r \le 50 000\)
\(0 \lt s \le 200 000 000, r\) – количество красных точек
На вход Вашей программы поступают данные в следующем формате:
СТРОКА 1: Содержит целое число \(g\).
СЛЕДУЮЩИЕ \(g\) СТРОК: Каждая строка содержит два целых числа – координаты \(x_i\) и \(y_i\) каждой из \(g\) зеленых точек, начиная с точки с номером 1 и заканчивая точкой с номером \(g\). Эти два числа разделены пробелами.
СТРОКА \(g\) + 2: Содержит целое число \(r\).
СЛЕДУЮЩИЕ \(r\) СТРОК: Каждая строка содержит два целых числа – координаты \(x_i\) и \(y_i\) каждой из \(r\) красных точек, начиная с точки с номером 1 и заканчивая точкой с номером \(r\). Эти два числа разделены пробелами.
Ваша программа должна вывести (\(g\) – 1) + (\(r\) – 1) строк, каждая из которых описывает один отрезок, соединяющий две точки.
Каждая строка должна содержать два целых числа и один символ, разделенные пробелом. Числа представляют
собой номера точек, соединенных этим отрезком. Если точки зеленые, то последним символом в строке должен быть \(g\), если точки красные, то последним символом в строке должен быть \(r\).
Ни порядок, в котором выводятся отрезки, ни порядок точек в строке не имеют значения.
Если существует несколько маршрутов товароперевозок, удовлетворяющих всем указанным требованиям, выведите любой из них.
Первая группа тестов: гарантируется, что решения корректно работающие при \(n + m \le 5000\) будут набирать не менее 37 баллов.
Вторая группа тестов: в ней 9 тестов, каждый оценивается независимо в 7 баллов.
3 0 5 5 5 2 1 3 0 0 5 0 3 4
Загрузить архив проверяющих библиотек
В игру «черный ящик» играют с помощью квадратного черного ящика, который располагается на плоском столе. На каждой из сторон ящика есть n отверстий (всего 4n отверстий), в которые можно вбрасывать шар. Вброшенный шар через некоторое время вылетит наружу через одно из 4n отверстий, возможно, через то же отверстие, в которое он был вброшен.
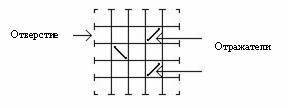
Содержимое черного ящика можно рассматривать в виде сетки размером n x n. Отверстия в сторонах ящика – это начала и концы строк и столбцов сетки. Каждая клетка сетки либо пустая, либо занята отражателем. Отражатель – это устройство, которое изменяет направление движения шара на 90 градусов. Рассмотрим пример ящика размером 5x 5.
Вброшенный шар движется по прямой, пока не попадает в отражатель или не вылетит наружу. Когда шар попадает в отражатель, шар меняет направление своего движения, а отражатель меняет свое положение (под словом «меняет» подразумевается поворот на 90 градусов). На примере показаны действия отражателя.
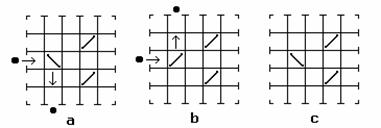
a)
Первый шар вброшен через отверстие. Он попал в отражатель и изменил направление движения.
b)
После попадания первого шара отражатель изменил свое положение. Новый шар вбросили в то же отверстие, он попал в тот же отражатель, и отразился в направлении, противоположном направлению первого шара после отражения.
c)
Отражатель изменил свое положение. После каждого попадания положение отражателя изменяется.
Когда шар попадает в отражатель, раздается звуковой сигнал. Количество отражений шара можно узнать, посчитав количество сигналов. Можно доказать, что шар всегда вылетает из ящика. У ящика есть одна кнопка, которая приводит его в исходное положение, и другая кнопка, которая меняет положение всех отражателей на противоположное.
ЗАДАНИЕ
Вам будет предоставлен интерфейс к 15 черным ящикам с помощью библиотеки функций Pascal
или C/C++. Вы должны определить содержимое каждого из ящиков как можно точнее и отправить на проверку файлы, описывающие каждый ящик. Интерфейс также предоставляет возможность создания собственных ящиков для тестирования.
ОГРАНИЧЕНИЯ
1 ≤ n ≤ 30
ВЫВОД
Вы должны предоставить на проверку файлы, содержащие следующие данные для каждого из 15 черных ящиков:
|
blackboxK.out |
ОПИСАНИЕ |
|
#FILE blackbox K ..... .../. .... .../. .?.?. |
СТРОКА 1: Заголовок файла, который должен иметь вид #FILE blackbox K где K (число в диапазоне 1..15) соответствует ящику, для которого найдено решение. n СТРОК:
Каждая строка описывает строку ящика, начиная с верхней и заканчивая нижней. Каждая строка должна содержать ровно n
символов, соответствующих клеткам, находящимся на пересечении этой строки и столбцов (слева направо).
·
Символ ‘.’ обозначает, что клетка пуста.
·
Символ ‘/’ обозначает, что в клетке находится отражатель с исходным положением ‘/’
·
Символ ‘’ обозначает, что в клетке находится отражатель с исходным положением ‘’
·
Символ ‘?’ обозначает, что Вы не смогли определить исходное содержимое клетки |
БИБЛИОТЕКА
Вам будет предоставлена библиотека, которая содержит следующие функции:
|
ФУНКЦИЯ |
Описание |
|
PASCAL function Initialize(box: integer): integer; C/C++ int Initialize(int box); |
Инициализирует библиотеку. Эта функция должна вызываться один раз в начале программы. Она возвращает значение n
– количество отверстий на каждой стороне ящика. Параметр box
должен содержать целое число в пределах от 1 до 15, указывающее номер ящика, который Вы хотите использовать, или 0, если Вы хотите использовать ящик, созданный Вами.
|
|
PASCAL function throwBall(holeIn, sideIn: integer; var holeOut, sideOut: integer): longint; C int throwBall(int holeIn, int sideIn, int *holeOut, int *sideOut); C++ int throwBall(int holeIn, int sideIn, int &holeOut, int &sideOut); |
Вбрасывает шар в ящик через отверстие с номером holeIn на стороне sideIn.
Стороны пронумерованы следующим образом: 1 – Верхняя, 2 – Правая, 3 – Нижняя и 4 – Левая. Отверстия пронумерованы слева направо и сверху вниз, начиная с номера 1 на каждой стороне. В параметрах holeOut
и sideOut
функция возвращает номер отверстия и номер стороны – место, где шар вылетел наружу. В качестве своего значения функция throwBall
возвращает количество звуковых сигналов, вызванных попаданиями шара в отражатели.
|
|
PASCAL procedure ResetBox; C/C++ Void ResetBox(); |
Возвращает все отражатели в исходное положение. |
|
PASCAL procedure ToggleDeflectors; C/C++ Void ToggleDeflectors(); |
Меняет положения всех отражателей в ящике на противоположные. |
|
PASCAL procedure Finalize; C/C++ Void Finalize(); |
Корректно заканчивает взаимодействие с ящиком. Эта функция должна вызываться в конце Вашей программы. |
Чтобы использовать библиотеку в Вашей программе, необходимо выполнить следующее:
·
FreePascal: В каталоге задачи есть файлы pbblib
.o и pbblib.
ppu. Чтобы их использовать, необходимо добавить следующую строку в Вашу программу
uses pbblib;
В файле pblackbox.pas представлен пример использования библиотеки.
·
C: В каталоге задачи есть файлы
cbblib.o и
cbblib.h. Чтобы их использовать, необходимо добавить следующую директиву в Вашу программу
#include “cbblib.h”
В файле cblackbox.c
представлен пример использования библиотеки. Чтобы скомпилировать код, используйте следующую команду
gcc –o yourprogram cbblib.o yourprogram.c
·
C++: В каталоге задачи есть файлы
cppbblib.o
и cppbblib.h. Чтобы их использовать, необходимо добавить следующую директиву в Вашу программу
#include “cppbblib.h”
В файле cppblackbox
.cpp представлен пример использования библиотеки. Чтобы скомпилировать код, используйте следующую команду
g++ –o yourprogram cppbblib.o yourprogram.cpp
ЗАМЕЧАНИЕ: В любой момент времени может быть запущено не более одной программы, работающей с библиотекой.
ПРИМЕР ВЗАИМОДЕЙСТВИЯ
Ниже представлен пример взаимодействия с ящиком, изображенным ранее на рисунке:
|
ВЫЗОВ ФУНКЦИИ |
ВОЗВРАЩЕННОЕ ЗНАЧЕНИЕ |
|
Initialize(0); |
Пусть программа взаимодействует с ящиком, изображенным на рисунке. Тогда функция возвращает значение 5, означая, что n
= 5.
|
|
PASCAL throwBall(3,4,holeOut,sideOut
);
C throwBall(3,4,&holeOut,&sideOut); C++ throwBall(3,4,holeOut,sideOut); |
Шар вбрасывается в отверстие с номером 3 (третье сверху) на левой стороне. Возвращается значение 1 – это означает, что шар отразился один раз. После возврата из функции, переменная holeOut
содержит значение 2, а переменная sideOut
содержит значение 3, то есть шар вылетел через отверстие с номером 2 (второе слева) нижней стороны ящика.
|
ЭКСПЕРИМЕНТИРОВАНИЕ
Если Вы передадите значение 0 в функцию Initialize, библиотека прочитает содержимое ящика из файла
blackbox.in. Так Вы сможете экспериментировать с библиотекой. Формат
файла blackbox.in
описан ниже.
|
blackbox.in |
ОПИСАНИЕ |
|
5 3 2 3 4 2 / 4 4 / |
СТРОКА 1: Содержит целое число n,
которое задает количество отверстий на каждой стороне. СТРОКА 2: Содержит целое число d
, которое задает количество отражателей в ящике.
СЛЕДУЮЩИЕ d СТРОК:
Каждый отражатель описывается одной строкой. Каждая строка содержит два целых числа, разделенных пробелом, которые задают номер столбца и строки, где расположен отражатель. После второго числа через один пробел записан
символ, который может быть ‘/’ или ‘’ и определяет исходное положение отражателя.
|
ЗАМЕЧАНИЕ: Файл blackbox.
in из примера описывает ящик, изображенный вверху страницы 1.
СООБЩЕНИЯ ОБ ОШИБКАХ
В случае любых проблем библиотека выведет сообщение об ошибке в стандартный поток вывода ошибок. Возможные сообщения об ошибке и их значения приведены в нижеследующей таблице.
|
СООБЩЕНИЕ |
ЗНАЧЕНИЕ |
|
ERR 1 More than one app |
Только одна программа может одновременно работать с черными ящиками, перезапустите все программы и запускайте их строго по одной. |
|
ERR 2 Invalid box |
Переданный вами номер ящика не лежит в пределах от 0 до 15. |
|
ERR 3 Invalid deflector |
В файле blackbox.in находится отражатель в некорректной клетке. |
|
ERR 4 Invalid symbol |
В файле blackbox.in обнаружен недопустимый символ. |
|
ERR 5 Invalid size |
Размер ящика в файле blackbox.
in задан неверно. |
|
ERR 6 Invalid input hole |
Либо сторона, либо отверстие вбрасывания шара заданы неверно. |
|
ERR 7 ALARM |
Пожалуйста, обратитесь к техническому персоналу. |