В ток-шоу принимают участие N знакомых между собой людей, среди которых могут быть те, которые всегда говорят неправду, а остальные всегда говорят правду (по крайней мере один человек). В конце программы ведущий решил определить, кто из участников к какой из групп принадлежит. Для этого он задал вопрос: «Сколько среди вас тех, кто всегда говорит правду?». Каждый из участников дал ответ: число от 0 до N. После этого ведущий может отобрать определенных людей, задать им тот же самый вопрос, и, получив ответ, гарантированно определить, кто из участников ток-шоу говорит правду, а кто лжет. Участники отвечают на второй вопрос относительно выбранных ведущим людей.
Напишите программу, которая по количеству участников ток-шоу и их ответам на первый вопрос найдет минимальное количество людей, которое нужно выбрать ведущему для второго этапа опроса.
Первая строка входного файла содержит одно целое число N (1≤N≤1000) – количество участников ток-шоу. Следующая строка содержит N целых чисел от 0 до N – ответы каждого из участников на первый вопрос.
Единственная строка выходного файла должна содержать целое число – искомое минимальное количество участников, которое необходимо выбрать ведущему для повторного опроса. В случае, если ведущий имеет возможность определить лжецов и тех, кто всегда говорит правду, уже после первого этапа опроса, нужно вывести число 0.
4 3 1 3 3
2
3 1 2 3
0
Клуб активного туризма на планете Олимпия решил предложить клиентам маршрут вдоль живописного хребта. Хребет достаточно длинный и его трудно пройти сразу, поэтому в клубе ищут самый привлекательный из маршрутов ограниченной длины. Согласно результатам социального исследования туристы любят проходить по местам, которые выше чем другие на как можно большем промежутке, благодаря более широкому обзору и эйфории от ощущения высоты.
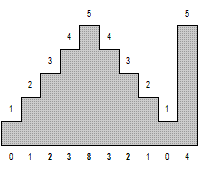
Для упрощения задачи хребет разделили на однометровые отрезки и определили среднюю высоту над уровнем моря каждого из них. Численное значение привлекательности каждого такого отрезка хребта равно количеству последовательных отрезков слева и справа, начиная с непосредственных его соседей, которые имеют высоту строго меньшую чем он сам. Сам отрезок в эту сумму не входит. Привлекательность маршрута вычисляется как сумма привлекательностей однометровых отрезков хребта, которые в него входят. Длина маршрута должна быть не больше чем T метров. Направление маршрута значения не имеет, поскольку не меняет его привлекательности. Маршрут может начинаться с любого отрезка хребта. Маршрут не может содержать разрывов, то есть в маршрут можно включать только последовательные отрезки хребта.
Напишите программу, которая по информации о высоте над уровнем моря каждого однометрового отрезка горного хребта вычислит привлекательность наиболее привлекательного маршрута длины не больше чем T метров.
Первая строка входного файла содержит два целых числа N – длина всего хребта в метрах и T (1≤T≤N≤100 000) – ограничение на длину маршруту. Вторая строка файла содержит N целых чисел от 1 до 106 – высоты последовательных однометровых отрезков.
Единственная строка выходного файла должна содержать одно целое число – численное значение привлекательности самого привлекательного маршрута вдоль горного хребта длины не более чем T.
На рисунке изображен хребет, который соответствует входным данным, разбитый на 10 отрезков. Числа сверху соответствуют высоте каждого из отрезков, а числа снизу – привлекательности соответствующего отрезка.
Решения, работающие для случая \(NT < 4 \cdot 10^6\) будут оцениваться из 40 баллов
10 5 1 2 3 4 5 4 3 2 1 5
18
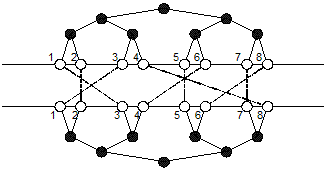На плоскости расположены два полных бинарных дерева глубины N. Их 2x2N листьев расположены на двух параллельных прямых и пронумерованы слева направо. Листья с одинаковыми номерами в первом и втором деревьях находятся один напротив другого. Между листьями деревьев задано соответствие – каждый из листьев одного дерева имеет ровно один соответствующий ему лист во втором дереве, и наоборот. На рисунке такие соответствия заданы прямыми отрезками между листьями. Такую конструкцию – два дерева вместе с соответствиями между листьями – называют танглеграмом. Танглеграмы, например, используются биологами при исследовании взаимосвязей генов разных видов растений.
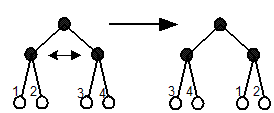Танглеграм тяжело исследовать, если многие из отрезков-соответствий пересекаются. Для того, чтобы уменьшить количество пересечений, разрешается осуществлять единственную операцию: в первом (верхнем) дереве можно менять местами два поддерева произвольной вершины, как изображено на втором рисунке.
Напишите программу, которая по информации о соответствии между листьями двух деревьев определит наименьшее возможное количество пересечений отрезков в графическом представлении танглеграма, которое может быть достигнуто путем выполнения операций обмена смежных поддеревьев первого дерева. Если в одной точке пересекаются больше двух отрезков, то под количеством пересечений нужно понимать количество попарных пересечений отрезков. Например, на первом рисунке соответствия 4-8, 5-5 и 6-4 образуют три пересечения.
В первой строке входного файла находится натуральное число N (1≤N≤19) – глубина деревьев. Вторая строка содержит 2N разных целых чисел от 1 до 2N, каждое i-ое из которых задает лист второго дерева, который связан отрезком с i-ым листом первого дерева.
Единственная строка выходного файла должна содержать наименьшее возможное количество пересечений отрезков-соответствий в танглеграме, которое может быть достигнуто путем обмена поддеревьев в первом дереве.
3 3 2 1 8 5 4 7 6
6
>Во время исследований, посвященных появлению жизни на планете Олимпия, учеными было сделано несколько сенсационных открытий:
- Все живые организмы планеты происходят от бактерии Bitozoria Programulis.
- Эволюция происходила шаг за шагом (по предположению ученых – во время изменения климата на планете).
- На каждом шаге эволюции из каждого вида образовывались ровно два подвида, а предыдущий вид исчезал.
- Если считать появление бактерии Bitozoria Programulis первым шагом эволюции, то существующие сейчас живые организмы находятся на N-ом шаге.
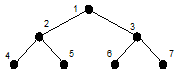
Чтобы не придумывать названия во время исследований, ученые пронумеровали все виды организмов, которые когда-либо существовали на планете. Для этого они нарисовали дерево эволюции с корнем Bitozoria Programulis, которая получила номер 1. Далее нумеровали виды каждого шага эволюции слева направо. Таким образом непосредственные подвиды Bitozoria Programulis получили номера 2 и 3. Следующими были занумерованы виды третьего шага эволюции – подвиды вида 2 получили номера 4 и 5, а вида 3 – номера 6 и 7, и т.д.
Напишите программу, которая по номерам двух видов вычислит номер вида их ближайшего общего предка в дереве эволюции.
Первая строка входного файла содержит целое число N (1≤N≤100) – количество этапов эволюции, которые произошли на планете Олимпия до текущего времени. Вторая и третья строки файла содержат по одному натуральному числу, которые представляют номера видов, для которых требуется найти номер их ближайшего общего предка.
Единственная строка выходного файла должна содержать натуральное число – номер ближайшего предка для двух видов.
4 15 12
3
18 233016 233008
14563
Торговец владеет тремя видами товаров: алмазы, яблоки и шелк. Для каждого товара известна стоимость в золотых монетах за единицу веса и его количество у торговца.
В стране, где живет торговец, есть N городов, которые пронумерованы от 1 до N. Родной город торговца имеет номер 1, а столица – номер N. Чтобы добраться до столицы, где торговец может продать товар, ему нужно проехать определенным маршрутом через другие города. Между некоторыми парами городов существуют дороги, проезд по которым стоит определенного количества золотых. В каждом городе взимается налог за провоз каждого из видов товара, заданный в процентах от стоимости провезенного через город товара. Известно, что выехав из любого города, торговец не может в него вернуться. Любые два города соединены не более чем одной дорогой.
Задача торговца получить наибольшую прибыль – разницу полученных в столице денег за проданный товар и расходов на путешествие в столицу. Он не обязан брать с собой весь свой товар. Торговец всегда имеет достаточно золотых для уплаты налогов, и не может рассчитаться товаром, который он везет в столицу. Все дороги ведут только в одном направлении.
Напишите программу, которая по информации о количестве единиц веса разных видов товара у торговца, цене на эти товары в столице, налогах в городах, дорогах между городами и стоимости проезда по этим дорогам установит максимальную прибыль, которую может получить торговец от реализации товара.
Первая строка входного файла содержит два целых числа N (2≤N≤500) и M (M≤1) – количество городов и дорог между ними. Вторая строка содержит три целых неотрицательных числа, которые соответствуют количествам единиц веса алмазов, яблок и шелка, принадлежащим торговцу. Третья строка содержит три целых неотрицательных числа – стоимости единиц веса алмазов, яблок и шелка соответственно. Последующие строки с 4-ой по N+1 содержат по три целых числа от 0 до 100 включительно, которые соответствуют процентам от стоимости алмазов, яблок и шелку, которые взимаются, соответственно, в городах от 2 до N-1 в качестве налога. В списке городов не учтены родной город торговца 1 и столица N, так как в них с торговца не взимают налог. Последующие M строк содержат по три целых неотрицательных числа, первые два из которых от 1 до N задают пару городов, между которыми проложена дорога, а третье – стоимость проезда по этой дороге. Дороги ведут в направлении от города, указанного первым, до того, который указан вторым. Количества единиц веса каждого из видов товара у торговца, стоимости товаров и цены проезда по дорогам не превышают 100.
Единственная строка выходного файла должна содержать одно число – точное значение найденной максимальной прибыли от поездки в столицу. Ответ всегда должен содержать ровно два знака после точки. В случаях, когда торговец не может получить прибыль или добраться до столицы по существующим дорогам, требуется вывести 0.00
4 4 10 5 20 100 5 12 15 40 25 90 20 10 1 2 5 1 3 10 3 4 10 2 4 15
1025.00