Темы --> Информатика --> Алгоритмы --> Алгоритмы поиска --> Бинарный поиск
    Бинарный поиск в массиве(24 задач)
    Бинарный поиск по ответу(56 задач)
    Бинарный поиск значения функции(5 задач)
---> 3 задач <---
Источники --> Командные олимпиады --> Командные чемпионаты школьников Санкт-Петербурга по программированию
    1999(5 задач)
    2000(7 задач)
    2001(8 задач)
    2002(8 задач)
    2003(9 задач)
    2004(9 задач)
    2005(10 задач)
    2006(10 задач)
    2007(10 задач)
    2008(9 задач)
    2009(10 задач)
    2010(10 задач)
    2011(9 задач)
    2012(10 задач)
    2013(10 задач)
    2014(11 задач)
    2015(11 задач)
    2016(11 задач)
Страница: 1 Отображать по:
#1126
Трамвайная остановка
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes
На прямой расположены остановки с заданными координатами. Заданы скорость трамвая и мальчика. Требуется найти минимальное расстояние L до первой остановки, на которое мальчик должен видеть приближение трамвая так, чтобы трамвай не обогнал его между остановками.

Трамвайная линия имеет вид прямой. Петя живет в N трамвайных остановках от метро. Метро находится у нулевой остановки, в точке с координатой 0.


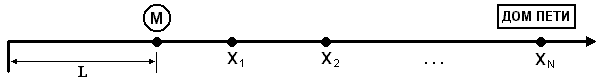
Выходя из метро, Петя хочет попасть домой как можно быстрее, но он очень не любит ждать трамвай на остановке. Поэтому, если, подходя к очередной трамвайной остановке, он не видит трамвая, то идет пешком вдоль трамвайной линии. Если в какой-то момент Петя видит трамвай, то он может принять решение вернуться на остановку, или продолжить свое движение к следующей остановке. Петя идет со скоростью U, трамвай едет со скоростью V. Нужно найти минимальное расстояние L, которое должно просматриваться перед нулевой остановкой, чтобы он мог идти со своей скоростью в сторону дома, не опасаясь, что трамвай его обгонит между остановками.

Входные данные

Во входном файле находятся три числа N, U и V (N ≤ 1000, U и V – положительные вещественные), за которым будет следовать N вещественных чисел – X1, X2,... Xn (0 < X1 < X2 < … < Xn < 106), разделенных пробелами.

 

Выходные данные

В выходной файл ваша программа должна вывести число L с точностью до 10-4.

Примеры
Входные данные
1 1 10
2
Выходные данные
9.0000
#1771
Свечки
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes
На круглом торте расположены свечки, заданные двумя координатами. Разрезы торта заданы уравнениями прямых. Требуется определить, есть ли на каком-либо кусочке торта более одной свечки.

Мише исполнилось \(n\) лет. Праздничный торт, испеченный по этому случаю, имеет форму круга радиуса \(r\) с центром в начале координат. На торте стоят \(n\) свечек. Мишина мама разделила торт на части, сделав \(m\) прямолинейных разрезов. Каждый гость взял один из получившихся кусков.

Миша хочет узнать, не досталось ли кому-нибудь из его гостей более одной свечки. Помогите ему это выяснить.

Входные данные

Первая строка входного файла содержит целые числа \(n\), \(m\) и \(r\) (1 ≤ \(n\) ≤ 10000, 0 ≤ \(m\) ≤ 1000, 1 ≤ \(r\) ≤ 2000).

Следующие n строк содержат пары целых чисел \(x_i\), \(y_i\) – координаты точек, где расположены свечки. Гарантируется, что эти точки лежат внутри круга, размерами свечек следует пренебречь. Никакие две свечки не совпадают.

Последние \(m\) строк содержат описание разрезов – тройки целых чисел \(a_i\), \(b_i\), \(c_i\). Такая тройка соответствует разрезу, который задается уравнением \(a_i\) \(x\) + \(b_i\) \(y\) + \(c_i\) = 0. Ни один разрез не проходит через свечку. Никакие два разреза не совпадают. Числа ai, bi, ci не превышают 10000 по модулю.

Выходные данные

Если одному из гостей досталось более одной свечки, выведите в выходной файл слово «YES», иначе выведите слово «NO».

Примеры
Входные данные
3 2 3
2 2
1 -1
-2 0
2 -1 0
0 1 -1
Выходные данные
NO
Входные данные
3 2 3
2 2
1 -1
-2 0
1 1 -1
0 1 -1
Выходные данные
YES
Входные данные
4 2 10
1 1
1 -1
-1 1
-1 -1
0 1 0
1 0 0
Выходные данные
NO
#1780
Атака инопланетян
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

На город Энск нападает флот инопланетян. Флот состоит из n космических кораблей, каждый из которых имеет форму равнобедренного прямоугольного треугольника.

Носом инопланетного корабля считается вершина, угол при которой прямой, а осью корабля называется высота, опущенная на гипотенузу.

Флот инопланетян прилетел с северо-востока, и застыл в таком положении, что все оси кораблей направлены строго на юго-запад.

Единственный способ нанести урон инопланетной армии – это пустить из некоторой точки поверхности Земли лазерный луч вертикально вверх. Пущенный так луч прожигает насквозь все вражеские корабли, через которые он проходит (даже те, которые он задевает по границе). Но этот выстрел повредит инопланетянам только в случае, если все n кораблей будут при этом поражены.

Военные власти города Энска решили нанести удар по вражеским войскам. Для этого решено поставить лазеры в одну из точек, над которыми находятся все n вражеских кораблей.

Помогите военным определить площадь территории, на которой можно поставить лазер.

Входные данные

В первой строке входного файла содержится целое число \(n\) – количество инопланетных кораблей (1 ≤ \(n\) ≤ 100).

В каждой из следующих n строк описывается положение очередного корабля. Описание состоит из трех целых чисел \(x_i\), \(y_i\) и \(s_i\), где \(x_i\) и \(y_i\) – координаты носа, а \(s_i\) – размер корабля. Поскольку корабль имеет форму равнобедренного прямоугольного треугольника, размером корабля военные решили называть длину катета.

Размеры кораблей – положительные числа, не превышающие 1 000. Координаты носов кораблей не превышают по абсолютной величине \(10^5\).

Выходные данные

В выходной файл выведите площадь территории, над которой находятся все инопланетные корабли. Выведите ответ с точностью до трех знаков после десятичной точки.

Примеры
Входные данные
3
2 4 6
4 2 7
3 3 5
Выходные данные
4.500
Страница: 1 Отображать по:
Выбрано
:
Отменить
|
Добавить в контест