Алгоритм Флойда(20 задач)
Обход в ширину(62 задач)
Алгоритм Форда-Беллмана(6 задач)
Зал супермаркета имеет форму прямоугольника размером \(M\) x \(N\), в котором расставлены витрины размером 1 x 1. Стороны витрин параллельны стенам супермаркета, а расстояния от витрин до стен – целые числа.
В супермаркет привезли новую супервитрину размером \(K\) x 1 и выгрузили в одном из углов супермаркета. Требуется передвинуть ее в противоположный угол супермаркета. При этом ее нельзя поворачивать, а можно лишь передвигать параллельно
стенам супермаркета. Напишите программу, которая по плану супермаркета поможет определить, какое наименьшее количество витрин нужно убрать, чтобы передвинуть супервитрину.
В первой строке вводятся три натуральных числа \(M\), \(N\) и \(K\) (\(M\), \(N\) ≤ 100, \(K\) ≤ \(M\)). Начальное и конечное расположение супервитрины такие, как указано на верхнем рисунке. В следующей строке записано целое неотрицательно число \(V\) – количество витрин (0 ≤ \(V\) ≤ \(N\)*\(M\)). В следующих \(V\) строках входных данных содержатся различные пары целых неотрицательных чисел, характеризующие положения витрин. Первое число (от 0 до \(M\)–1) – расстояние от левой стены супермаркета до витрины, второе (от 0 до \(N\)–1) – расстояние от нижней стены до витрины (см. нижний рисунок). Гарантируется, что там, где изначально поставили супервитрину, других витрин нет.
В первой строке выведите минимальное количество витрин, которые необходимо убрать. Во второй строке выведите возможный маршрут передвижения супервитрины: одну строку из заглавных латинских букв, обозначающих следующее:
U – на 1 вверх,
D – на 1 вниз,
L – на 1 влево,
R – на 1 вправо.
Количество символов в строке не должно превышать \(N\) x \(M\).
Если возможных маршрутов несколько, то выведите любой из них.
10 10 5 0
0 RUURUURUURUURU
9 3 2 4 2 0 5 1 5 2 8 2
1 URRRDRRRRUU
На клеточном поле введена система координат так, что центр координат находится в точке пересечения линий сетки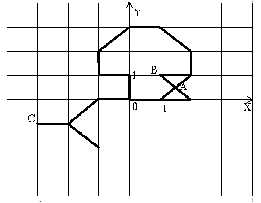 и оси направлены вдоль линий сетки.
и оси направлены вдоль линий сетки.
На этом поле выложили связную фигуру, состоящую из спичек. Использовались спички двух типов:
Ребенок хочет сжечь фигуру. При этом он может поджечь ее в одной точке, имеющей целочисленные координаты (например, в точке A на рисунке поджигать фигуру нельзя, а в точках B и C — можно).
Известно, что огонь распространяется вдоль спички равномерно (но по каждой спичке — со своей скоростью). Спичка может гореть в нескольких местах (например, когда она загорается с двух концов; или когда в середине диагональной спички огонь перекидывается с одной спички на другую — огонь расползается по вновь подожженной спичке в обе стороны).
Напишите программу, которая определит, в какой точке нужно поджечь фигуру, чтобы она сгорела за минимальное время.
Во входном файле записано сначала число N — количество спичек (1N40). Затем идет N пятерок чисел вида X1, Y1, X2, Y2, T, задающих координаты концов спички и время ее сгорания при условии, что она будет подожжена с одного конца (гарантируется, что каждая спичка имеет длину 1 или , все спички образуют связную фигуру, и положение никаких двух спичек не совпадает). Все координаты — целые числа, по модулю не превышающие 200, время сгорания — натуральное число, не превышающее 107.
Выведите координаты целочисленной точки, в которой нужно поджечь фигуру, чтобы она сгорела за наименьшее время, а затем время, за которое в этом случае фигура сгорит. Время должно быть выведено с точностью не менее 2-х знаков после десятичной точки. Если решений несколько, выведите любое из них.
1 0 0 1 1 1
0 0 1.00
5 0 0 0 1 1 1 0 0 1 10 0 0 1 0 1 0 0 1 1 1 2 2 1 1 1
0 0 3.25
3 1 1 1 2 10 1 2 2 2 10 1 1 2 2 50
2 2 35.00
Эпидемия гриппа не обошла стороной семиклассника Алешу. Скучая дома, Алеша решил вырезать фигурки из листа клетчатой бумаги. Лист состоял из M строк и N столбцов клеточек. Сначала Алеша нарисовал на листе границы фигур. Количество фигур было не меньше 2. Чтобы фигуры получались ровными, границы фигур Алеша рисовал строго по линиям имеющейся клеточной разметки листа (при этом некоторые границы фигур могли пройти по границам листа). Форма фигур могла быть любой, но при этом все фигуры были связными (фигура называется связной, если из любой ее клетки можно добраться до любой другой, ходя только по клеткам фигуры и перемещаясь каждый раз в одну из 4-х соседних по стороне клеток). Никакие две фигуры не имели общих точек, в том числе не касались углами клеток.
<>Затем Алеша вырезал нарисованные фигуры, делая разрезы только по их границам. При этом оставшаяся часть листа осталась связной (то есть не распалась на несколько частей).Лист с вырезами Алеша отсканировал. Сканер в своей памяти по результатам сканирования построил таблицу, состоящую из нулей и единиц, из M строк и N столбцов (строки нумеруются сверху вниз от 1 до M, столбцы — слева направо от 1 до N). Каждый элемент таблицы соответствовал клеточке исходного листа. Единица обозначала, что соответствующая клетка листа осталась на месте, ноль — соответствующая клетка была вырезана.
На рис. 1 приведен пример клетчатого листа, а на рис. 2 — соответствующая ему таблица в памяти сканера:
|
Рис 1. Исходный клеточный лист с вырезанными фигурами Размер листа: M=6, N=12. Количество вырезанных фигур: 3
|
Рис 2. Такая таблица строится в памяти сканера
|
После этого сканер представил полученную таблицу в специальном, описанном ниже формате и передал информацию на компьютер. Напишите программу, которая по полученной информации установит:
Пункт 1. Сколько клеток было вырезано из листа?
Пункт 2. Сколько фигур было вырезано?
Описание формата представления таблицы
Последовательность подряд идущих по горизонтали или вертикали единиц будем называть полосой. Полосу можно задаеть 4 числами:
Всю таблицу разобьем на полосы, состоящие из единиц так, чтобы каждая единица принадлежала хотя бы одной полосе. При этом полосы могут пересекаться, а также накладываться. Таким образом, таблица представляется в виде описания всех полос, которое удовлетворяет трем дополнительным требованиям:
Заметим, что таблица может быть представлена в виде полос разными способами, но каждое представление позволяет однозначно восстановить таблицу.
Во входном файле записано сначала число \(P\) (1 или 2) — номер пункта задачи, ответ на который требуется получить. Далее записаны размеры исходного листа — числа \(M\) и \(N\) \((1 \le M \le 4000, 1 \le N \le 4000)\). Затем записано число \(K\) \((0 \le K \le 256000)\) — количество полос в описании полученной таблицы. Затем идет K четверок чисел, описывающих полосы (полосы перечисляются в порядке начальных клеток полос: по строкам сверху вниз, в строке — слева направо).
В выходной файл выведите искомое количество (если \(P=1\), то — количество клеток, вырезанных из листа, если \(P=2\), то — количество фигур, вырезанных из листа).
1 40 400 2 1 1 100 40 0 1 101 1
15959
2 40 400 2 1 1 100 40 1 1 101 1
2