На вокзале есть K тупиков, куда прибывают электрички. Этот вокзал является их конечной станцией, поэтому электрички, прибыв, некоторое время стоят на вокзале, а потом отправляются в новый рейс (в ту сторону, откуда прибыли).

Дано расписание движения электричек, в котором для каждой электрички указано время ее прибытия, а также время отправления в следующий рейс. Электрички в расписании упорядочены по времени прибытия. Поскольку вокзал — конечная станция, то электричка может стоять на нем довольно долго, в частности, электричка, которая прибывает раньше другой, отправляться обратно может значительно позднее.

Тупики пронумерованы числами от 1 до K. Когда электричка прибывает, ее ставят в свободный тупик с минимальным номером. При этом если электричка из какого-то тупика отправилась в момент времени X, то электричку, которая прибывает в момент времени X, в этот тупик ставить нельзя, а электричку, прибывающую в момент X+1 — можно.

Напишите программу, которая по данному расписанию для каждой электрички определит номер тупика, куда прибудет эта электричка.

В ежегодном чемпионате Флатландии (которая, естественно, является плоским миром) по космическим гонкам "Формула-3" участвуют N космических скутеров, имеющие форму треугольников. До начала гонок скутеры занимают положение в стартовой зоне согласно результатам жеребьевки.

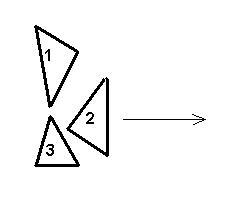
Скутеры стартуют строго по порядку. Каждый скутер,получив команду «старт», уезжает в положительном направлении оси Ox. Следующий скутер стартует лишь тогда, когда предыдущий покинет стартовую зону. Скутеры уезжают строго параллельно оси Ox, скутеры в стартовой зоне не поворачивают и не разворачиваются.

Естественно, что если в момент старта на пути скутера окажется другой скутер, то произойдет авария (даже если скутер заденет лишь угол другого скутера своим углом).

Для уменьшения опасности столкновения скутеров на старте строго соблюдается следующее правило: прямые, параллельные оси Ox и пересекающие какой-то скутер, должны в совокупности пересекать не более 100 других скутеров (прямая, проходящая через одну точку скутера также считается прямой, пересекающей скутер). Например, на приведенном рисунке прямые, параллельные Ox и пересекающие скутер 2, проходят через 2 других скутера (1 и 3), а прямые, проходящие через скутер 1, проходят только через один другой скутер (номер 2).

Главный Судья гонок хочет определить порядок, в котором должны стартовать скутеры, чтобы аварии не произошло. Например, в ситуации, приведенной на рисунке, сначала должен стартовать скутер номер 2 (если попытается стартовать скутер номер 1 или 3, то он столкнется со скутером номер 2). После этого скутеры 1 и 3 могут стартовать в любом порядке (они друг другу не мешают).

Помогите Главному Судье — напишите программу, которая определит какой-нибудь порядок старта скутеров, чтобы аварии не произошло.

Вася нарисовал выпуклый \(N\)-угольник и провел в нем несколько диагоналей таким образом, что никакие две диагонали не пересекаются внутри \(N\)-угольника. Теперь он утверждает, что весь \(N\)-угольник оказался разбит на треугольники. Напишите программу, которая проверяет истинность Васиного утверждения.

Палиндром - это строка, которая читается одинаково как справа налево, так и слева направо.

На вход программы поступает набор больших латинских букв (не обязательно различных). Разрешается переставлять буквы, а также удалять некоторые буквы. Требуется из данных букв по указанным правилам составить палиндром наибольшей длины, а если таких палиндромов несколько, то выбрать первый из них в алфавитном порядке.

В программе Microsoft Excel имеется возможность сортировки таблицы по значениям какого-нибудь столбца. В процессе сортировки переставляются целиком строки таблицы (а не только значения в столбце, по которому осуществляется сортировка). При этом используется устойчивая сортировка, то есть если в этом столбце в нескольких строках стоят одинаковые значения, то эти строки после сортировки будут расположены в том же порядке, что и до сортировки (т.е. раньше будет идти та строка, которая до сортировки шла раньше).

Вася последовательно сортировал всю таблицу несколько раз. Вам дана последовательность номеров столбцов, по которым Вася сортировал таблицу — в этой последовательности один и тот же столбец мог встречаться несколько раз, например, если Вася отсортировал ее сначала по 1-му столбцу, потом по 2-му, а затем снова по 1-му.

Вам требуется написать программу, которая определит, можно ли было как-то оптимизировать последовательность сортировок так, чтобы результат не изменился (независимо от содержания таблицы). Например, если последовательность состоит из двух сортировок по столбцу 1, то можно оставить только одну такую сортировку.