Массивы(232 задач)
Типы данных(356 задач)
Циклы(177 задач)
Условный оператор (if)(164 задач)
Python(260 задач)
Standard Template Library(2 задач)
В комнате у Аркадия Семеновича Тапкина стоят электронные часы. Цифры на этих часах показываются в специальной псевдографике. А именно, каждое поле, на котором изображается цифра, состоит из w ячеек в ширину и h ячеек в высоту (при этом ячейки на поле имеют форму квадратов).
Но недавно у Аркадия Семеновича появилась проблема. Последнее время он стал плохо видеть. В связи с этим он хочет увеличить изображение этих цифр. Он уже приладил старый 19'' монитор к часам, и теперь дело осталось за малым. Осталось написать программу, которая будет рисовать цифры на дисплее. Аркадий Семенович хочет увеличить изображение в k раз и сделать толщину линий равной d. Помогите ему в этом.
Опишем более формально понятие «увеличить в k раз». Занумеруем ячейки поля w×h сверху вниз и слева направо. Таким образом, верхняя левая ячейка имеет координаты (0, 0), правая нижняя – (w - 1, h - 1), правая верхняя – (w - 1, 0), левая нижняя – (0, h - 1). Кроме этого, введем декартову прямоугольную систему координат так, что начало координат находится в центре верхней левой ячейки, ось Ox направлена вправо, ось Oy – вниз, длину единичного отрезка примем равной длине стороны ячейки. Таким образом, координаты центра ячейки совпадают с ее координатами во введенной нумерации.
Каждая десятичная цифра задается набором составляющих ее изображение отрезков. Для простоты каждый из отрезков либо параллелен одной из координатных осей, либо идет под углом в 45 градусов к ней.
Увеличенная в k раз цифра рисуется на поле размером (w - 1) . (k - 1) + w ячеек по горизонтали на (h - 1) . (k - 1) + h ячеек по вертикали.
При увеличении некоторой цифры в k раз производятся следующие операции. Координаты точек, являющихся концами отрезков, составляющих цифру, умножаются на k. После этого закрашиваются те ячейки, через центры которых проходят эти отрезки. Эти ячейки будем называть основными.
После этого, для того, чтобы получить толщину линий равную d, дополнительно закрашиваются те ячейки, центры которых располагаются на расстоянии, не превышающем (d - 1) от центров основных ячеек. Расстоянием между точками A(xA, yA) и B(xB, yB) будем называть число ![]() (A, B) = | xA - xB| + | yA - yB|.
(A, B) = | xA - xB| + | yA - yB|.
По описанию цифры и параметрам k и d выведите изображение цифры, увеличенное в k раз, с толщиной линий d.
В первой строке вводятся числа k и d ( 1![]() k
k![]() 100, 1
100, 1![]() d
d![]() 500). Вторая строка содержит целые числа w и h ( 1
500). Вторая строка содержит целые числа w и h ( 1![]() w, h
w, h![]() 10).
10).
В третьей строке задается целое число n ( 1![]() n
n![]() 100) – количество отрезков в описании цифры. Далее следуют n строк, каждая из которых описывает один отрезок. Описание отрезка состоит из четырех целых чисел: x1, y1, x2, y2 ( 0
100) – количество отрезков в описании цифры. Далее следуют n строк, каждая из которых описывает один отрезок. Описание отрезка состоит из четырех целых чисел: x1, y1, x2, y2 ( 0![]() x1, x2 < w, 0
x1, x2 < w, 0![]() y1, y2 < h) – координат концов отрезка.
y1, y2 < h) – координат концов отрезка.
Каждый из отрезков либо параллелен одной из координатных осей, либо идет под углом в 45 градусов к ней. Все отрезки имеют ненулевую длину.
Программа должна вывести ровно (h - 1) . (k - 1) + h строк по (w - 1) . (k - 1) + w символов в каждой, j-ый символ i-ой строки должен быть равен символу «*» (звездочка), если ячейка с центром в точке (j, i) закрашена, и символу «.» (точка) – иначе.
1 1 4 6 2 0 0 3 0 3 0 3 5
**** ...* ...* ...* ...* ...*
2 1 4 6 4 0 0 3 0 3 0 3 2 3 2 0 5 0 5 3 5
******* ......* ......* ......* ......* .....*. ....*.. ...*... ..*.... .*..... *******
Максимальное время работы на одном тесте: 2 секунды
При разработке программ для просмотра веб-страниц одной из наиболее сложных задач является корректное отображение таблиц. Компания «Kozilla», в которой вы работаете, планирует разработать новую версию браузера «Waterrat» для работы в терминальном режиме и просит вас написать фрагмент ядра отображения веб-страниц, ответственный за формирование структуры таблиц.
Фрагмент, который вы должны написать, получает на вход информацию о количестве строк таблицы и ячейках этих строк и должен сгенерировать структуру таблицы и передать ее модулю, который занимается отображением таблицы на экране.
Таблица состоит из строк, каждая строка состоит из одной или нескольких ячеек, j-я ячейка i-й строки имеет ширину ai, j.
По заданным параметрам таблицы постройте символическое изображение ее структуры.
В первой строке вводится число n – количество строк в таблице ( 1![]() n
n![]() 100). Каждая из следующих n строк входных данных описывает одну строку таблицы.
100). Каждая из следующих n строк входных данных описывает одну строку таблицы.
Описание строки включает число mi – количество ячеек в этой строке, и mi целых чисел ai, 1, ai, 2,..., ai, mi – ширину каждой из ячеек строки ( 1![]() mi
mi![]() 10, 1
10, 1![]() ai, j
ai, j![]() 20).
20).
Выведите символическое изображение структуры таблицы.
Изображение i-й строки таблицы должно начинаться горизонтальной линией, составленной из символов «+» (плюс) и «-» (минус). Затем должна следовать строка, содержащая пробелы и символы «|» (вертикальная черта). Первым символом строки должна быть вертикальная черта, затем ai, 1 пробелов, затем вертикальная черта, затем ai, 2 пробелов, и так далее, всего mi блоков пробелов. После последнего блока должна следовать вертикальная черта.
После последней строки таблицы также должна следовать горизонтальная линия.
В изображении горизонтальной линии используйте символ «+», если сверху или снизу от этой позиции находится вертикальная черта, и «-» в противном случае. Горизонтальная черта должна иметь минимальную возможную длину, чтобы над каждым символом вертикальной черты следующей строки и под каждым символом вертикальной черты предыдущей строки были символы «+».
4 3 3 5 1 1 2 1 2 2 5 1
+---+-----+-+ | | | | +--++-----+-+ | | +--+ | | +--+--+-+ | | | +-----+-+
Неудовлетворенный стандартным календарем своей операционной системы, Витя решил написать программу, которая будет выводить красиво отформатированный календарь. Он разработал формальные требования к календарю, но понял, что сам не способен написать соответствующую программу. Помогите ему.
Календарь состоит из блоков, каждый из которых соответствует одному месяцу. Блоки расположены в виде таблицы из k столбцов и 12/k строк (k выбирается делителем числа 12). Месяцы выводятся в следующем порядке: первая строка содержит блоки, соответствующие месяцам с первого по k-ый, следующая – с (k + 1)-го по 2k-ый, и т. д.
Ширина всех блоков в столбце должна быть одинакова, высота всех блоков равна семи (числу дней в неделе). Между блоками различных строк таблицы выводится пустая строка, в каждой строке между соседними блоками из разных столбцов выводится три пробела.
Блок, соответствующий месяцу, устроен следующим образом. Каждой (в том числе неполной) неделе данного месяца в блоке соответствует столбец, имеющий ширину, равную двум. Между двумя соседними столбцами в каждой строке выводится один пробел. Если несколько блоков располагаются в одном столбце календаря, то для выравнивания ширины в те блоки, которые содержат меньше недель, в конец добавляется необходимое число пустых столбцов-недель. При этом разные столбцы календаря могут иметь разную ширину.
Все числа месяца заносятся в блок, соответствующий этому месяцу. Число заносится строку блока, соответствующую дню недели, на который приходится число в этом месяце. Число заносится в столбец блока, соответствующий неделе, к которой относится данное число. Однозначные числа дополняются слева одним пробелом. Таким образом, числа в столбце оказываются выравнены по правому краю.
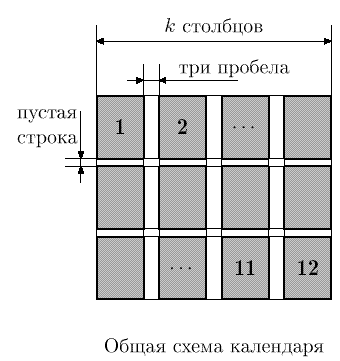 | 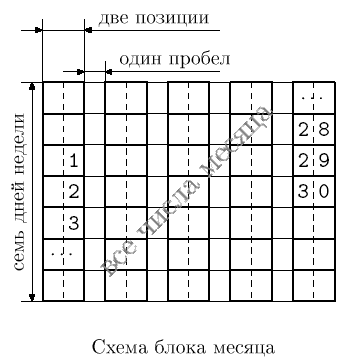 | |
| Общая схема календаря | Схема блока месяца |
На вход прораммы поступает описание года, календарь для которого следует вывести. Оно содержит три числа: d – день недели, на который приходится первое января ( 1![]() d
d![]() 7), l – является ли год високосным (l = 1 означает, что год является високосными, l = 0 – что не является) и k – количество столбцов в календаре (k – одно из чисел 1, 2, 3, 4, 6, 12).
7), l – является ли год високосным (l = 1 означает, что год является високосными, l = 0 – что не является) и k – количество столбцов в календаре (k – одно из чисел 1, 2, 3, 4, 6, 12).
Напомним, что високосный год отличается от обычного тем, что в високосном году февраль содержит 29 дней.
Выведите календарь, отформатированный в соответствии с условием задачи. Проверяющая программа в этой задаче игнорирует пробелы в конце строк. В остальном календарь должен быть отформатирован в точности так, как описано в условии.
4 1 4
5 12 19 26 2 9 16 23 1 8 15 22 29 5 12 19 26
6 13 20 27 3 10 17 24 2 9 16 23 30 6 13 20 27
7 14 21 28 4 11 18 25 3 10 17 24 31 7 14 21 28
1 8 15 22 29 5 12 19 26 4 11 18 25 1 8 15 22 29
2 9 16 23 30 6 13 20 27 5 12 19 26 2 9 16 23 30
3 10 17 24 31 7 14 21 28 6 13 20 27 3 10 17 24
4 11 18 25 1 8 15 22 29 7 14 21 28 4 11 18 25
3 10 17 24 31 7 14 21 28 5 12 19 26 2 9 16 23 30
4 11 18 25 1 8 15 22 29 6 13 20 27 3 10 17 24 31
5 12 19 26 2 9 16 23 30 7 14 21 28 4 11 18 25
6 13 20 27 3 10 17 24 1 8 15 22 29 5 12 19 26
7 14 21 28 4 11 18 25 2 9 16 23 30 6 13 20 27
1 8 15 22 29 5 12 19 26 3 10 17 24 31 7 14 21 28
2 9 16 23 30 6 13 20 27 4 11 18 25 1 8 15 22 29
6 13 20 27 4 11 18 25 1 8 15 22 29 6 13 20 27
7 14 21 28 5 12 19 26 2 9 16 23 30 7 14 21 28
1 8 15 22 29 6 13 20 27 3 10 17 24 1 8 15 22 29
2 9 16 23 30 7 14 21 28 4 11 18 25 2 9 16 23 30
3 10 17 24 1 8 15 22 29 5 12 19 26 3 10 17 24 31
4 11 18 25 2 9 16 23 30 6 13 20 27 4 11 18 25
5 12 19 26 3 10 17 24 31 7 14 21 28 5 12 19 26
Ваня очень любит шахматы. Причем он не только любит просто играть в шахматы, но часто придумывает разные головоломки и просто забавные задачки с использованием шахматных фигур. Также вместо стандартной шахматной доски 8×8 Ваня часто использует в своих задачах доски другого размера.
Недавно он придумал новую головоломку и рассказал ее своим друзьям. Суть головоломки заключается в следующем. На одно из полей доски размером m×n записывается некоторое положительное целое число и затем на него ставится ферзь.
После этого Ваня делает k ходов ферзем, каждый раз перемещая его по шахматным правилам на одно из полей, на котором он еще не был. При этом каждый раз, перед тем как поставить ферзя на некоторое поле, он записывает на это поле целое число, причем это число всегда больше всех чисел, уже записанных на доске.
Задача друзей Вани – по числам, записанным на доске, восстановить маршрут ферзя или выяснить, что Ваня где-то ошибся. Поскольку Ваня часто выбирает достаточно большие m, n и k, друзья устали решать эту головоломку вручную и решили написать для ее решения программу. Помогите им
Напомним, что по шахматным правилам ферзь может пойти на любое поле доски, находящееся на одной вертикали, горизонтали или диагонали с тем полем, на котором он находится.
В первой строке вводятся числа m, n и k ( 1![]() m, n
m, n![]() 300, 0
300, 0![]() k < mn). Следующие m строк содержат по n целых чисел и описывают поля доски (пустому полю соответствует число 0, а полю, на котором записано число – это число). Все числа, записанные на доске, положительные, целые и не превышают 109.
k < mn). Следующие m строк содержат по n целых чисел и описывают поля доски (пустому полю соответствует число 0, а полю, на котором записано число – это число). Все числа, записанные на доске, положительные, целые и не превышают 109.
Если Ваня ошибся при построении головоломки, выведите сообщение «Wrong Board».
В противном случае выведите m строк по n чисел – для каждого поля выведите номер хода, перед которым ферзь побывал на этом поле, а для последнего поля, на котором он оказался – число k + 1. Для полей, на которые ферзь не попадал, выведите число 0.
4 4 7 10 20 0 100 30 0 0 40 0 0 0 0 45 42 0 70
1 2 0 8 3 0 0 4 0 0 0 0 6 5 0 7
2 4 4 10 20 30 40 0 50 0 0
Wrong Board
2 2 2 1 2 4 3
Wrong Board
Год назад Флатландию потряс серьезный экономический кризис, после которого, с целью снижения издержек, фермер Джон и фермер Билл решили объединить свои фермы. За год совместной продуктивной работы на объединенной территории было построено четыре сарая.
Однако последствия кризиса в последнее время ощущаются все меньше, да и совместное ведение хозяйства – дело непростое. Поэтому фермеры решили снова разделить свои фермы.
Для раздела ферм решено было построить забор. Разумеется, прежде чем приступить к строительству, фермеры взяли карту совместного хозяйства и стали обсуждать возможное положение забора. Забор должен представлять собой прямую линию. Поскольку по закону границы участков должны быть направлены либо с севера на юг, либо с запада на восток, забор на карте должен представлять собой прямую, параллельную краю карты – вертикальную либо горизонтальную.
Единственная проблема – четыре построенных за год совместной работы сарая. Разумеется, каждому фермеру в результате раздела должно достаться по два сарая. Поэтому после постройки забора два сарая должны оказаться с одной стороны от него, а два других – с другой.
Помогите фермерам найти такое положение для забора. Забор может проходить непосредственно вдоль стены сарая.
На вход программы поступают четыре четверки целых чисел. Каждая четверка описывает один сарай. Первые два числа в описании сарая – это координаты на карте его левого нижнего угла, следующие два числа – координаты правого верхнего угла.
Система координат размещена таким образом, что ось OX направлена слева направо, а ось OY – снизу вверх. Оси координат параллельны краям карты. Стороны сараев также параллельны краям карты. Сараи не имеют общих точек. Каждый сарай имеет ненулевую площадь. Все координаты неотрицательны и не превышают 109.
Если построить забор, удовлетворяющий всем условиям, невозможно, выведите слово «Impossible».
В противном случае в первой строке выведите слово «Vertical», если забор следует построить параллельно вертикальному краю карты, или слово «Horizontal», если забор следует построить параллельно горизонтальному краю карты.
В следующей строке выведите координату x всех точек забора, если он должен быть вертикальным, либо координату y всех точек забора, если он должен быть горизонтальным. Выведенная координата должна быть целым числом (несложно показать, что если забор можно построить, то его можно построить так, чтобы искомая координата была целой).
Приведенные ниже рисунки соответствуют примерам входных данных.
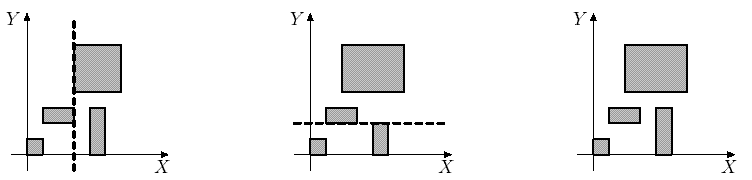
0 0 1 1 1 2 3 3 4 0 5 3 3 4 6 7
Vertical 3
0 0 1 1 1 2 3 3 4 0 5 2 2 4 6 7
Horizontal 2
0 0 1 1 1 2 3 3 4 0 5 3 2 4 6 7
Impossible