#191

Шахматный детектив

Темы: [Динамическое программирование: два параметра] [Перебор с отсечением]

Источники: [ Командные олимпиады, ВКОШП, 2006, Задача A ]

Дано изображение состоящее из черных, белых и серых клеток. Необходимо определить, может ли изображение быть шахматной доской (клетки доски могут состоять из нескольких маленьких клеток).

Известный частный сыщик поставил чашку с чаем на специальную подогревающую подставку, питающуюся от USB-порта его компьютера, и приступил к обдумыванию очередного запутанного преступления. Через пару часов раздумий он понял, что для разгадки этого дела достаточно определить, была ли на месте преступления шахматная доска.

Недавно он получил по электронной почте фотографию места преступления. Подозрительный фрагмент (тот, на котором изображен предмет, похожий на шахматную доску) уже был скопирован в отдельный файл, но вдруг выяснилось, что, поскольку фотография была сжата с потерей качества, некоторые пиксели на ней из белых или черных стали серыми. Таким образом, определение того, является ли сфотографированный предмет шахматной доской, стало намного более сложным.

Все усложняется тем, что на фотографию могла попасть не вся шахматная доска, а лишь ее часть. Например, на приведенном рисунке на фотографию попала часть доски, у которой каждое поле имеет длину стороны, равную трем пикселям.

Помогите частному сыщику в расследовании преступления. Напишите программу, которая определит, может ли заданный фрагмент фотографии быть изображением части шахматной доски, и, если может, восстановит изображение шахматной доски до сжатия.

Шахматная доска – это квадрат, разбитый на x² (для некоторого x) равных квадратов – полей. Стороны полей параллельны сторонам изображения. Длина стороны каждого поля шахматной доски выражается целым числом пикселей. Все пиксели, принадлежащие одному полю, покрашены в один и тот же цвет – черный или белый. При этом соседние поля (поля, имеющие общую сторону) покрашены в различные цвета.

Входные данные

В первой строке вводятся два целых числа: m и n – размеры фрагмента фотографии в пикселях ( 1 $le$ m, n $le$ 250).

Следующие m строк содержат по n символов каждая, j-й символ i-й строки соответствует пикселю с координатами (i, j). Символ «.» (точка) означает белый пиксель, символ «*» – черный, символ «?» – серый.

Выходные данные

Если заданный фрагмент фотографии может быть изображением части шахматной доски, выведите слово «YES». После этого выведите m строк по n символов в каждой – изображение соответствующей части шахматной доски в том же формате, что и во входных данных, только серые пиксели должны быть заменены на белые или черные. Если решений несколько, выведите любое.

В противном случае программа должна вывести слово «NO».

Примеры

Входные данные

4 5
*.?.?
.***.
.*?*.
.*?*.

Выходные данные

YES
*...*
.***.
.***.
.***.

Входные данные

4 5
..?..
.***.
.*?*.
.*?*.

Выходные данные

NO

#409

Максимальная сумма

Темы: [Динамическое программирование на таблицах]

Источники: [ Командные олимпиады, ВКОШП, 2006, Задача G ]

Задана таблица, содержащая числа. Необходимо найти прямоугольную рамку (прямоугольник, с осями, параллельными осям координат и шириной линий 1) с максимальной суммой чисел в ячейках, покрытых рамкой.

Сегодня на страницах газеты «Математический досуг» была опубликована необычная математическая головоломка. Одна из страниц газеты полностью занята прямоугольной таблицей, состоящей из m строк и n столбцов. В каждой ячейке таблицы записано некоторое целое число.

Для решения головоломки требуется найти такой невырожденный прямоугольник с вершинами в центрах ячеек таблицы, и сторонами, параллельными сторонам таблицы, чтобы сумма чисел, записанных в ячейках на границе получившегося прямоугольника, была максимальна.

Безуспешно потратив несколько часов на решение головоломки, Саша решил написать программу, которая сделала бы это за него. Но и тут его постигла неудача. Теперь ему ничего не остается, как обратиться за помощью к вам.

Напишите программу, которая по заданной таблице найдет искомый прямоугольник.

Входные данные

В первой строке вводятся два целых числа $m$ и $n$ ($2 \le m, n \le 300$). Далее следует описание таблицы – $m$ строк, каждая из которых содержит по $n$ целых чисел $a_{i, j}$ ($-10^4 \le a_{i,j} \le 10^4$).

Выходные данные

В первой строке выведите целое число $s$ – максимальную сумму чисел на границе искомого прямоугольника. Во второй строке выведите четыре натуральных числа: $x_1$, $y_1$, $x_2$, $y_2$ – координаты левой верхней и правой нижней ячейки выбранного прямоугольника, соответственно (здесь $x$ – номер строки, а $y$ – номер столбца, строки нумеруются сверху вниз, начиная с единицы, столбцы нумеруются слева направо, начиная с единицы). Если оптимальных решений несколько, выведите любое.

Примеры

Входные данные

2 3
1 1 1
1 1 1

Выходные данные

6
1 1 2 3

Входные данные

5 4
9 -2 -1 3
-10 -5 1 -4
1 -1 2 -2
3 0 0 -1
2 2 -1 2

Выходные данные

8
3 1 5 3

#415

Эксперимент

Темы: [Динамическое программирование на графах]

Источники: [ Командные олимпиады, ВКОШП, 2005, Задача C ]

Задано дерево зависимостей частей эксперимента (т.е. какие действия необходимо выполнить до данного). Также для каждого действия определено, на какой установке (всего 2) оно делается. Требуется определить порядок действия, чтобы минимизировать количество переходов между установками.

Сегодня Игорь получил долгожданное разрешение на проведение эксперимента по изучению протекания химических реакций в магнитном поле. При этом используются две установки – генератор магнитного поля и манипулятор, соединяющий реагенты.

Эксперимент разбит на некоторое количество этапов, при этом некоторые из них могут быть выполнены только после завершения определенного набора других этапов. Правда известно, что хотя бы один способ проведения эксперимента существует. На каждом этапе Игорь должен управлять ровно одной из двух установок – либо генератором, либо манипулятором.

Игорь очень дорожит своим временем, и поэтому он хочет провести эксперимент, совершив наименьшее количество перемещений между пультами управления установками. Помогите ему узнать, в каком порядке следует выполнять этапы, чтобы этого добиться.

Входные данные

В первой строке вводится целое число n – количество этапов эксперимента ( 1 $le$ n $le$ 100).

Следующие n строк содержат описание этапов. Пронумеруем этапы от 1 до n в некотором произвольном порядке. Тогда i-я из этих строк описывает i-й этап. Каждый этап описывается последовательностью целых чисел. Первое число равно нулю, если на этом этапе Игорь управляет генератором, и единице, если он управляет манипулятором. Затем записано целое число r_i – количество этапов, которые должны быть выполнены перед выполнением данного. За ним следуют номера этих этапов – r_i различных целых чисел в диапазоне от 1 до i - 1.

Выходные данные

В первой строке выведите минимальное количество перемещений, которые придется совершить Игорю. Во второй строке выведите перестановку чисел от 1 до n – последовательность, в которой следует выполнять этапы. Если решений несколько, выведите любое.

Примеры

Входные данные

Выходные данные

1
2 1 3

#420

Красно-черные деревья

Темы: ["Длинная" арифметика] [Динамическое программирование на графах]

Источники: [ Командные олимпиады, ВКОШП, 2005, Задача H ]

Задано дерево. Каждый узел может покрасить в красный или черный цвет так, чтобы не было двух соединенных красных вершин и количество красных вершин на пути от корня до листьев было одинаковым. По заданному дереву требуется определить количество корректных способов раскраски дерева.

Широкое распространение в стандартных библиотеках многих языков программирования получила реализация сбалансированных деревьев на основе так называемых красно-черных деревьев. В данной задаче вам предлагается посчитать количество красно-черных деревьев заданной формы.

Напомним, что двоичным деревом называется набор вершин, организованных в виде дерева. Каждая вершина имеет не более двух детей, один из которых называется левым, а другой – правым. Как левый, так и правый ребенок, а также оба могут отсутствовать.

Если вершина Y – ребенок вершины X, то говорят, что вершина X является родителем вершины Y. У каждой вершины дерева, кроме одной, есть ровно один родитель. Единственная вершина, не имеющая родителя, называется корнем дерева.

Соединим каждую вершину, кроме корня, с ее родителем. Заметим, что для каждой вершины существует ровно один путь, ведущий в нее от корня.

Двоичное дерево называется красно-черным, если каждая его вершина раскрашена в красный либо в черный цвет, причем выполняются следующие условия:

если вершина красная, то ее родитель – черный;
количество черных вершин на пути от корня до любой вершины, у которой отсутствует хотя бы один ребенок, одно и то же.

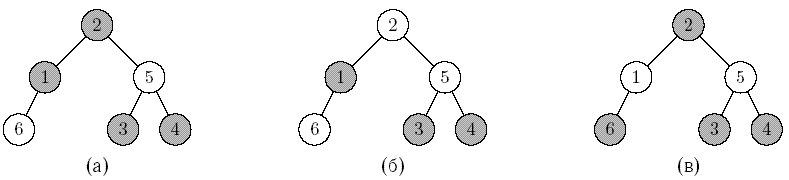
Примеры двоичного дерева, вершины которого раскрашены в два цвета, приведены на следующем рисунке.

Если считать закрашенные вершины черными, а незакрашенные – красными, то дерево на рисунке (а) является красно-черным деревом, а деревья на рисунках (б) и (в) – нет. Для дерева на рисунке (б) нарушается первое свойство – у красной вершины 5 родитель 2 также красный, а в дереве на рисунке (в) нарушается второе свойство – на пути от корня до вершины 1 одна черная вершина, а, например, на пути от корня до вершины 3 – две.

Для заданного двоичного дерева подсчитайте число способов раскрасить его вершины в черный и красный цвет так, чтобы оно стало красно-черным деревом.

Входные данные

В первой строке вводится число n – количество вершин в дереве ( 1 $le$ n $le$ 1000).

Пусть вершины дерева пронумерованы числами от 1 до n. Следующие n строк содержат по два числа – для каждой вершины заданы номера ее левого и правого ребенка. Если один из детей отсутствует, то вместо его номера записан ноль. Гарантируется, что входные данные корректны, то есть набор вводимых чисел действительно задает двоичное дерево.

Выходные данные

Выведите одно число – количество способов раскрасить вершины заданного двоичного дерева в красный и черный цвета так, чтобы оно стало красно-черным деревом.

Примеры

Входные данные

Выходные данные

Входные данные

Выходные данные

#430

Нанокристалл

Темы: [Эвристические методы] [Динамическое программирование на графах]

Источники: [ Командные олимпиады, ВКОШП, 2004, Задача H ]

Взаимной удаленностью двух вершин невзвешенного графа называется кратчайшее расстояние между ними. Необходимо построить граф, в котором сумма взаимных удаленностей вершин равна задана числу.

Сверхсекретный завод, расположенный высоко в горах, занимается изготовлением новейших систем контроля торсионных полей – нанокристаллов. Нанокристалл состоит из нескольких атомов, некоторые из которых попарно связаны сверхпрочными торсионными связями.

Нанокристалл стабилен, если между любыми двумя его атомами можно построить соединяющую их цепочку связей, возможно с использованием других атомов. Например, нанокристалл $cal {X}$ из четырех атомов A, B, C и D, в котором между собой связаны пары A - B, A - C, B - C и B - D, стабилен. Если же, например, в нанокристалле из данных четырех атомов связаны только пары A - B и C - D, то кристалл нестабилен, поскольку, например, A и C не соединены никакой цепочкой связей.

Для любой пары атомов стабильного нанокристалла определена их взаимная удаленность – минимальная длина цепочки из связей, которая их соединяет. Например, рассмотрим описанный выше нанокристалл $cal {X}$ . Взаимная удаленность атомов A и B равна единице (они соединены напрямую), а взаимная удаленность C и D равна двум (они соединены цепочками C - B - D и C - A - B - D, длина кратчайшей цепочки равна двум).

Важнейшей характерикой стабильного нанокристалла является его емкость. Емкость нанокристалла равна сумме взаимных удаленностей всех пар его атомов. Например, емкость нанокристалла $cal {X}$ равна 8.

Недавно на завод поступил заказ – разработать стабильный нанокристалл заданной емкости c. При этом как число атомов в нанокристалле, так и число связей может быть произвольным. Помогите ученым разработать такой кристалл!

Входные данные

На вход программы поступает число c ( 1 $le$ c $le$ 10 000).

Выходные данные

В первой строке выведите два целых числа n и m – количество атомов и связей в разработанном нанокристалле, соответственно. Будем считать, что атомы нанокристалла пронумерованы от 1 до n. Следующие m строк должны содержать по два целых числа – пары атомов, которые следует соединить торсионными связями. Если решений несколько, выведите любое.

Если искомого нанокристалла не существует, выведите в первой и единственной строке выходных данных два нуля.

Примеры

Входные данные

Выходные данные

0 0

Входные данные

Выходные данные