Темы --> Информатика --> Алгоритмы --> Арифметические алгоритмы
    НОД и алгоритм Евклида(45 задач)
    Системы счисления(36 задач)
    "Длинная" арифметика(58 задач)
    Простые числа и разложение на множители(45 задач)
    Остатки(21 задач)
    Быстрое возведение в степень(3 задач)
    Быстрое преобразование Фурье(3 задач)
---> 4 задач <---
Источники --> Личные олимпиады --> Украинские олимпиады
    1999(3 задач)
    2000(5 задач)
    2001(4 задач)
    2002(7 задач)
    2003(3 задач)
    2004(6 задач)
    2005(5 задач)
    2006(6 задач)
    2007(6 задач)
    2008(5 задач)
    2009(6 задач)
    2010(0 задач)
    2011(0 задач)
    2012(0 задач)
    2013(0 задач)
    2016(5 задач)
Страница: 1 Отображать по:
#1346
ВТО
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

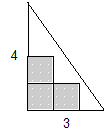Территория Великой Треугольной Области (ВТО) представляет собой прямоугольный треугольник. Длины его катетов равны M и N государственных единиц длины (ГЕД). Правительство ВТО решило покрыть как можно большую часть территории области квадратными плитами размером 11 ГЕД. Плиты должны плотно прилегать друг к другу и к катетам ВТО. Разрезать плиты нельзя.

Согласно межгосударственным соглашениям, правительство ВТО не имеет права покрыть частью своей плиты чужую территорию. Производитель поставляет плиты только контейнерными партиями — по P плит. Правительство заказывает столько контейнеров, сколько необходимо для реализации проекта.

Заведующий центральным складом, узнав про проект, решил, что его интересует коли­чество плит, которые останутся на складе из последнего контейнера после покрытия территории ВТО.

Напишите программу, которая по длинам катетов ВТО и вместимости контейнера находит количество плит, которые останутся на складе после осуществления проекта.

Входные данные

Единственная строка входного файла содержит три целых числа: M, N (2≤M, N≤2 000 000 000) и P (100≤P≤10 000).

Выходные данные

Единственная строка выходного файла должна содержать целое число — количество неиспользованных плит из последнего контейнера.

Примеры
Входные данные
4 3 100
Выходные данные
97
#1396
Эволюция
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

>Во время исследований, посвященных появлению жизни на планете Олимпия, учеными было сделано несколько сенсационных открытий:

  1. Все живые организмы планеты происходят от бактерии Bitozoria Programulis.
  2. Эволюция происходила шаг за шагом (по предположению ученых – во время изменения климата на планете).
  3. На каждом шаге эволюции из каждого вида образовывались ровно два подвида, а предыдущий вид исчезал.
  4. Если считать появление бактерии Bitozoria Programulis первым шагом эволюции, то существующие сейчас живые организмы находятся на N-ом шаге.

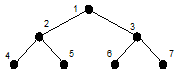
Чтобы не придумывать названия во время исследований, ученые пронумеровали все виды организмов, которые когда-либо существовали на планете. Для этого они нарисовали дерево эволюции с корнем Bitozoria Programulis, которая получила номер 1. Далее нумеровали виды каждого шага эволюции слева направо. Таким образом непосредственные подвиды Bitozoria Programulis получили номера 2 и 3. Следующими были занумерованы виды третьего шага эволюции – подвиды вида 2 получили номера 4 и 5, а вида 3 – номера 6 и 7, и т.д.

Напишите программу, которая по номерам двух видов вычислит номер вида их ближайшего общего предка в дереве эволюции.

Входные данные

Первая строка входного файла содержит целое число N (1≤N≤100) – количество этапов эволюции, которые произошли на планете Олимпия до текущего времени. Вторая и третья строки файла содержат по одному натуральному числу, которые представляют номера видов, для которых требуется найти номер их ближайшего общего предка.

Выходные данные

Единственная строка выходного файла должна содержать натуральное число – номер ближайшего предка для двух видов.

Примеры
Входные данные
4
15
12
Выходные данные
3
Входные данные
18
233016
233008
Выходные данные
14563
#1634
Спички
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

Какое минимальное количество спичек необходимо для того, чтобы выложить на плоскости \(N\) квадратов со стороной в одну спичку? Спички нельзя ломать и класть друг на друга. Вершинами квадратов должны быть точки, где сходятся концы спичек, а сторонами – сами спички.

Напишите программу, которая по количеству квадратов \(N\), которые необходимо составить, находит минимальное необходимое для этого количество спичек.

Входные данные

Единственная строка входного файла содержит одно целое число \(N\) (1≤\(N\)≤\(10^9\)).

Выходные данные

Единственная строка выходного файла должна содержать одно целое число – минимальное количество спичек требуемых для составления заданного количества квадратов.

Примеры
Входные данные
4
Выходные данные
12
#1639
Делители
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

По заданному натуральному числу N необходимо вычислить количество натуральных чисел, которые есть делителями N! (факториала числа N).

Например, при N=4, N!=4·3·2·1=24. Это число имеет следующие делители: 1, 2, 3, 4, 6, 8, 12, 24. Таким образом, искомое количество составляет 8.

Напишите программу, которая по натуральному N, находит количество делителей его факториала.

Формат входных данных

Единственная строка входного файла содержит одно целое число N (1≤N≤45).

Формат выходных данных

Единственная строка выходного файла должна содержать одно целое число –найденное количество делителей числа N!

Примеры
Входные данные
4
Выходные данные
8
Страница: 1 Отображать по:
Выбрано
:
Отменить
|
Добавить в контест