Вася записывает в клетки квадратной таблицы NxN натуральные числа по порядку, сначала заполняя первую строку слева направо, затем вторую и т.д. (см. рисунок слева). Петя заполняет такую же таблицу, расставляя числа сначала в первый столбец сверху вниз, затем во второй столбец и т.д.

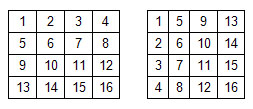
При этом оказалось, что некоторые числа и Вася, и Петя записали в одну и ту же клетку (например, число 6 записано во вторую строку второго столбца обеих таблиц).

Вам требуется написать программу, выводящую  все числа, которые в обеих таблицах записаны в одних и тех же клетках.

Многие натуральные числа можно представить в виде N = 3A + 5B, где A и B - целые неотрицательные числа. Например, 11=3x2+5x1, 20=3x0+5x4.

Вам требуется по заданному числу определить, можно ли его представить в таком виде, и если это возможно, найти подходящие A и B.

На прямой тропинке на расстоянии 1 метр друг от друга сидят два кузнечика. Время от времени один из кузнечиков прыгает на несколько сантиметров влево или вправо. Требуется узнать, каково было минимальное расстояние, на которое сближались кузнечики в процессе прыжков. (Расстояние считается только в те моменты, когда оба кузнечика сидят на земле).

Требуется сравнить два 100-значных числа.