Темы --> Информатика --> Алгоритмы --> Алгоритмы на графах --> Кратчайшие пути в графе --> Обход в ширину
    0-1 BFS(3 задач)
---> 3 задач <---
Источники --> Командные олимпиады --> Командные чемпионаты школьников Санкт-Петербурга по программированию
    1999(5 задач)
    2000(7 задач)
    2001(8 задач)
    2002(8 задач)
    2003(9 задач)
    2004(9 задач)
    2005(10 задач)
    2006(10 задач)
    2007(10 задач)
    2008(9 задач)
    2009(10 задач)
    2010(10 задач)
    2011(9 задач)
    2012(10 задач)
    2013(10 задач)
    2014(11 задач)
    2015(11 задач)
    2016(11 задач)
Страница: 1 Отображать по:
#1764
Два коня
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes
На шахматной доске находится два коня. Для них заданы начальные и конечные клетки. Требуется вывести минимальную последовательность ходов коней так, чтобы они не находились на одной и той же клетке.

Петя учится играть в шахматы. Недавно он заметил, что несмотря на то, что кони умеют прыгать через фигуры, они могут мешать друг другу дойти до нужных клеток. Петя поставил на доску двух коней: черного и белого, и для каждого их них выбрал клетку, на которой он хочет его видеть. Теперь ему интересно, какое минимальное число ходов потребуется коням, чтобы дойти до нужных клеток.

Кони ходят по шахматным правилам (на одну клетку по горизонтали и две по вертикали или на одну клетку по вертикали и на две по горизонтали). Порядок ходов черного и белого коня может быть произвольным. Коням не разрешается одновременно вставать на одну и ту же клетку.

Входные данные

Во входном файле записаны четыре клетки шахматной доски в следующем порядке: начальное положение белого коня, начальное положение черного коня, конечное положение белого коня, конечное положение черного коня. Клетка шахматной доски задается горизонталью (буква от «a» до «h») и вертикалью (цифра от 1 до 8), не разделенными пробелами. Описания клеток отделяются друг от друга одним пробелом.

Гарантируется, что исходно кони находятся на различных клетках, и в конце кони также должны оказаться на различных клетках.

Выходные данные

Выведите в первой строке выходного файла количество необходимых ходов. Далее выведите последовательность ходов. Ход описывается следующим образом: буква, соответствующая цвету коня («W» для белого или «B» для черного) и клетка, на которую нужно пойти. Клетку выведите в таком же формате, как во входном файле.

Если искомой последовательности ходов не существует, выведите на первой строке выходного файла число -1.

Примеры
Входные данные
a1 a2 a1 a6
Выходные данные
2
B b4
B a6
#1786
Лабиринт
  

Открыв глаза, Принц Персии обнаружил, что находится на верхнем уровне подземного лабиринта Джаффара. Лабиринт состоит из \(h\) уровней, расположенных строго друг под другом. Каждый уровень представляет собой прямоугольную площадку, разбитую на \(m\) × \(n\) участков. На некоторых участках стоят колонны, поддерживающие потолок, на такие участки Принц заходить не может.

Принц может перемещаться с одного участка на другой участок того же уровня, если у этих участков есть общая сторона, и ни один из этих участков не содержит колонну. Это перемещение занимает у Принца 5 секунд.

Полы в лабиринте Джаффара чрезвычайно тонкие, и Принцу не составляет труда сильным ударом ноги проломить пол под собой, если только на соответствующем участке нижнего уровня не находится колонна. Когда пол проламывается, Принц проваливается на один уровень вниз, при этом не перемещаясь в горизонтальной плоскости. Это действие также занимает у Принца 5 секунд. Конечно, если Принц уже находится на самом нижнем уровне, то пол под ним не проломится.

На одном из участков нижнего уровня Принца ждет Принцесса, отказавшаяся выйти замуж за злого Джаффара. Помогите Принцу найти Принцессу, потратив на это как можно меньше времени.

Входные данные

В первой строке входного файла содержатся натуральные числа \(h\), \(m\) и \(n\) – высота и горизонтальные размеры лабиринта (2 ≤ \(h\), \(m\), \(n\) ≤ 50). Далее во входном файле приведены \(h\) блоков, описывающих уровни лабиринта в порядке от верхнего к нижнему.

Каждый блок содержит \(m\) строк, по \(n\) символов в каждой: «.» (точка) обозначает свободный участок, «o» (строчная латинская буква «o») обозначает участок с колонной, «1» обозначает свободный участок, в котором оказался Принц в начале своего путешествия, «2» обозначает свободный участок, на котором томится Принцесса.

Символы «1» и «2» встречаются во входном файле ровно по одному разу: символ «1» – в описании самого верхнего уровня, а символ «2» – в описании самого нижнего.

Соседние блоки разделены одной пустой строкой.

Выходные данные

В выходной файл выведите минимальное время в секундах, необходимое Принцу, чтобы найти Принцессу. Поскольку Добро всегда побеждает Зло, гарантируется, что Принц может это сделать.

Примеры
Входные данные
3 3 3
1..
oo.
...

ooo
..o
.oo

ooo
o..
o.2
Выходные данные
60
#3409
Гонки
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

На день рождения юному технику Мише подарили машинку с радиоуправлением. Мише быстро наскучило гонять машинку туда-сюда по комнате, и он соорудил специальную трассу. Для этого он разбил комнату на квадратные ячейки, некоторые из них оставив пустыми, а в некоторые поставив препятствия. Целую неделю Миша каждый день улучшал свой рекорд по прохождению трассы. Но каково же было разочарование Миши, когда к нему в гости пришел Тима со своей машинкой и побил его рекорд. Стало понятно, что машинку необходимо модернизировать.

На пробных испытаниях, которые были произведены через день, Миша обнаружил, что машинка действительно ездит лучше, однако ее поведение несколько изменилось. На пульте теперь функционируют только четыре кнопки: вперед, назад, вправо, влево. При нажатии на них машинка едет по направлению к соответствующей стене комнаты, являющейся одновременно границей трассы, точно перпендикулярно ей. Машинка разгоняется до такой скорости, что перестает реагировать на другие команды, врезается в ближайшее препятствие или стену и отскакивает от нее на половину пройденного расстояния, то есть если между машинкой и стеной было x пустых клеток, то после отскока она остановится на клетке, от которой 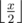клеток до стены (⌊ x⌋ означает округление вниз, например , ).

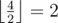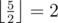Теперь Мише интересно, какое минимальное количество раз необходимо нажать на кнопку пульта, чтобы машинка, начав в клетке старта, остановилась в клетке финиша.

Входные данные

Первая строка входного файла содержит два целых числа n и m — размеры трассы (2 ≤ m, n ≤ 20). Следующие n строк содержат по m символов каждая: символ «.» соответствует пустой клетке, «#» — препятствию, а «S» и «T» — клетке старта и клетке финиша соответственно.

Выходные данные

В выходной файл выведите минимальное количество нажатий на кнопки пульта для проведения машинки по трассе от старта до финиша.

Если доехать от старта до финиша невозможно, выведите  - 1.

Примеры
Входные данные
5 5
S#..T
.#.##
.....
.##.#
.#...
Выходные данные
6
Страница: 1 Отображать по:
Выбрано
:
Отменить
|
Добавить в контест