Турнир Архимеда(52 задач)
Кировские командные турниры(8 задач)
Барнаульские командные турниры(10 задач)
Московская командная олимпиада(246 задач)
Командные чемпионаты школьников Санкт-Петербурга по программированию(167 задач)
ВКОШП(180 задач)
В подземелье есть N залов, соединенных туннелями. В некоторых залах находятся роботы, которые одновременно получили команду собраться в одном месте.
Роботы устроены так, что, получив команду, они все начали двигаться с такой скоростью, что туннель между двумя любыми залами преодолевают за 1 минуту. Роботы не могут останавливаться (в том числе и в залах), а также менять направление движения, находясь в туннелях (однако попав в зал, робот может из него пойти по тому же туннелю, по которому он пришел в этот зал).
Напишите программу, вычисляющую, через какое минимальное время все роботы смогут собраться вместе (в зале или в туннеле).
Сначала на вход программы поступают числа N — количество залов (1≤N≤400) и K — количество туннелей (1≤K≤20000). Далее вводится K пар чисел, каждая пара описывает номера залов, соединяемых туннелем (по туннелю можно перемещаться в обе стороны). Между двумя залами может быть несколько туннелей. Туннель может соединять зал с самим собой. Далее следует число M (1≤M≤400) — количество роботов. Затем вводятся M чисел, задающих номера залов, где вначале расположены роботы. В одном зале может быть несколько роботов.
Выведите минимальное время в минутах, через которое роботы могут собраться вместе. Если роботы никогда не смогут собраться вместе, выведите одно число –1 (минус один).
Оценка задачи
1 балл получат программы, правильно решающие задачу в случае, когда встреча роботов произойдет в зале, при ограничениях N≤100, K≤2000, M≤100.
4 5 1 2 2 3 3 4 1 4 1 3 3 1 2 4
1
3 2 1 2 2 3 2 1 3
1
На плоскости нарисовали прямоугольник, после чего его разрезали прямыми. Напишите программу, которая вычислит, сколько из полученных кусков исходного прямоугольника имеют треугольную форму.
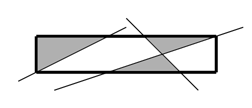
Рисунок, соответствующий 1-му примеру входных и выходных данных
Сначала на вход программы поступают два положительных числа X и Y, задающих координаты правого верхнего угла прямоугольника. Прямоугольник расположен в системе координат так, что левый нижний его угол имеет координаты 0,0 и стороны параллельны осям координат.
Далее вводится целое число N — количество разрезов (1≤N≤200). Затем описываются сами разрезы. Каждый разрез делался вдоль некоторой прямой. Каждая прямая, соответствующая разрезу, задается тремя числами A, B, C такими, что все точки (x,y) этой прямой (и только они) удовлетворяют уравнению Ax+By+C=0 (при этом всегда A2+B2>0).
Все входные данные (кроме N) – вещественные числа, заданы с двумя знаками после десятичной точки и не превышают 104. Никакие две прямые не совпадают между собой и не содержат сторон прямоугольника. Каждый разрез проходит через точки внутри исходного прямоугольника.
Выведите одно целое число — количество частей исходного прямоугольника, имеющих треугольную форму.
Система оценки
1 балл получат программы, правильно решающие задачу при ограничении 1≤N≤50.
5.00 1.00 3 1.00 -2.00 0.00 1.00 -3.00 -2.00 1.00 1.00 -4.00
3
4.00 2.00 2 1.00 -2.00 0.00 1.00 2.00 -4.00
4
Государство Флатландия представляет собой прямоугольник размером \(M\) × \(N\), состоящий из единичных квадратиков. Флатландия разделена на K провинций (2 <= \(K\) <= 100). Каждая провинция представляет собой связное множество квадратиков, т.е. из каждой точки провинции можно дойти до любой другой ее точки, при этом разрешается переходить с квадратика на квадратик, только если они имеют общую сторону (общей вершины недостаточно). Во Флатландии нет точки, которая граничила бы более чем с тремя провинциями (т.е. четыре квадратика, имеющие общую вершину, не могут принадлежать четырем разным провинциям).
Каждая провинция имеет свой символ. Столица Флатландии находится в провинции, которой принадлежит символ \(A\) (заглавная латинская буква \(A\)). Провинция называется пограничной, если она содержит граничные квадратики. Провинция, в которой находится столица Флатландии, не является пограничной.
Король соседнего с Флатландией королевства Ректилания решил завоевать Флатландию. Для этого он хочет захватить столицу Флатландии. Однако он знает, что сил его армии недостаточно, чтобы сделать это сразу. Поэтому сначала он хочет окружить столичную провинцию, чтобы ослабить силы противника долгой блокадой, а потом захватить столицу.
Чтобы окружить провинцию, требуется захватить все провинции, с которыми она граничит. Две провинции граничат, если существует два квадратика, имеющие общую сторону, один из которых принадлежит первой из них, а другой - второй. Чтобы захватить провинцию, надо чтобы выполнялось одно из двух условий: либо она пограничная, либо граничит с какой-либо уже захваченной провинцией.
Чтобы сберечь силы своей армии, король Ректилании хочет установить блокаду столичной провинции, захватив как можно меньше провинций. Помогите ему выяснить, сколько провинций требуется захватить. Захватывать столичную провинцию нельзя, поскольку для этого сил армии Ректилании пока недостаточно.
В первой строке вводятся числа \(M\) и \(N\) (3 <= \(M\), \(N\) <= 200). Следующие \(M\) строк содержат \(N\) символов каждая и задают карту Флатландии. Символ, находящийся в \(i\) + 1-й строке входных данных на \(j\)-м месте, представляет собой символ провинции, которой принадлежит квадратик (\(i\), \(j\)). Все символы имеют ASCII-код больше 32 (пробела).
Выведите единственное число - количество провинций, которые требуется захватить. Если установить блокаду невозможно, выведите "-1".
3 3 BBB BAB BBB
1
Дима обнаружил у папы на столе специальный чертежный прибор, похожий на циркуль - измеритель. Измеритель отличается от обычного циркуля тем, что в обеих его ножках находятся иголки (у обычного циркуля в одной ножке находится иголка, а в другой - грифель).
Дима взял клетчатый лист бумаги, установил между иглами измерителя некоторое расстояние, прочно зафиксировав его, и начал втыкать измеритель в лист бумаги. Каждый раз Дима втыкал в лист обе иглы измерителя, при этом он всегда делал это так, что дырочки получались в точках пересечениях линий, которыми лист разлинован на клетки. При этом в одну и ту же дырку Дима мог вставлять измеритель несколько раз.
Вечером папа нашел лист, с которым развлекался Дима, и решил выяснить, какое расстояние между иглами измерителя Дима мог установить. Все, что знает папа - координаты дырок, проделанных иглами измерителя. Помогите Папе решить поставленную задачу.
В первой строке вводится число \(n\) - количество дырок (2 <= \(n\) <= 1000). Следующие n строк содержат по два целых числа - координаты дырок. Координаты не превышают \(10^4\) по абсолютной величине.
В первой строке выведите \(k\) - количество различных расстояний, которые Дима мог установить между иглами измерителя. Следующие k строк должны содержать искомые расстояния, по одному вещественному числу в строке. Расстояния должны быть выведены в возрастающем порядке. Каждое число должно быть выведено с точностью не менее, чем 10-9.
Гарантируется, что существует по крайней мере одно расстояние, которое Дима мог установить между иглами измерителя.
4 0 0 1 1 1 0 0 1
2 1.0 1.4142135623730951
Прямоугольную таблицу, состоящую из N строк и M столбцов, раскрашивают следующим образом. Каждый столбец таблицы и каждую строку красят либо в синий, либо в желтый цвет. В итоге клетки, оказавшиеся на пересечении синего столбца и синей строки оказываются синими, желтого столбца и желтой строки — желтыми, а клетки на пересечении синего столбца и желтой строки, или, наоборот, желтого столбца и синей строки — зелеными.
Раскраска всех клеток таблицы (или просто сама таблица) называется правильной, если она может быть получена описанным выше способом.
Вам дана прямоугольная таблица, которую нужно раскрасить таким образом. Про некоторые клетки известно, какого цвета они должны быть, а остальные клетки могут в итоге быть любого цвета. Определите, сколько существует различных правильных таблиц, в которых нужные клетки покрашены в нужный цвет.
Вводятся числа N и M — количество строк и столбцов таблицы (1≤N≤30, 1≤M≤30). Далее записано N строк по M чисел в каждой, задающие цвета, в которые должны быть окрашены клетки:
0 — клетка может в итоге быть любого цвета
1 — клетка должна быть синей
2 — клетка должна быть желтой
3 — клетка должна быть зеленой
Выведите одно число — количество различных правильных таблиц, в которых нужные клетки покрашены в нужный цвет. Обратите внимание, что если два или более способов раскраски столбцов и строк таблицы приводят к одинаковой раскраске самой таблицы, то это нужно считать как один вариант раскраски таблицы (см. пример 2).
Примеры
| Входные данные | Выходные данные |
| 3 4 1 0 0 0 3 0 0 0 0 0 0 0 | 16 |
| 2 2 3 3 3 3 | 1 |
| 2 2 2 2 2 3 | 0 |