Элементарная геометрия(144 задач)
Многоугольники. Выпуклые оболочки(38 задач)
Клеточная геометрия(8 задач)
Квадродерево(3 задач)
Окружная олимпиада(18 задач)
Региональный этап(109 задач)
Заключительный этап(97 задач)
Король Полигонии Трианг IV помешан на реформах. Чтобы войти в мировую историю, он решил провести территориальную реформу в своей стране. Страна Полигония имеет форму простого многоугольника, то есть ее граница не имеет самопересечений и самокасаний. В Полигонии большую роль играют внутренние диагонали — отрезки, соединяющие вершины государственной границы и полностью проходящие по территории страны, не касаясь границы. При этом форма Полигонии такова, что никакие две внутренние диагонали не лежат на одной прямой.
Вместо традиционного деления государства на административные округа король Трианг IV решил разделить свою страну на административные треугольники внутренними диагоналями. Для сокращения управляющего аппарата король повелел подготовить такой план деления страны, в котором количество административных треугольников будет минимальным.
Требуется написать программу, выполняющую деление Полигонии внутренними диагоналями на минимально возможное число административных треугольников.
Формат входных данных
В первой строке входных данных задается число N (3 ≤ N ≤ 20) — количество вершин многоугольника, образующего границу Полигонии. В следующих N строках находятся по 2 целых числа, по абсолютной величине не превосходящих 10 000 — координаты вершин в порядке обхода многоугольника против часовой стрелки. Гарантируется, что никакие три последовательные вершины многоугольника не лежат на одной прямой, и он не имеет самопересечений и самокасаний. Также гарантируется, что никакие две диагонали, содержащиеся внутри многоугольника, не лежат на одной прямой.
Формат выходных данных
В первую строку выведите наименьшее количество административных треугольников, на которое можно разбить Полигонию.
Во вторую строку выведите количество различных внутренних диагоналей K, с помощью которых можно произвести данное разбиение.
В каждую из следующих K строк выведите 4 целых числа — координаты начала и конца соответствующей диагонали разбиения, полностью лежащей внутри многоугольника и не проходящей по его границе.
Если искомых разбиений несколько, выведите любое из них.
Примеры
|
Входные данные |
Выходные данные |
Рисунок к тесту |
|
4 |
2 |
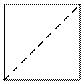 |
|
10 |
4 |
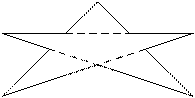 |
Горнолыжник, готовясь к соревнованиям, нарисовал на бумаге схему горнолыжной трассы для выбора оптимального маршрута спуска. На схеме расположенные на трассе ворота представлены горизонтальными отрезками. Никакая пара ворот не имеет общих точек.
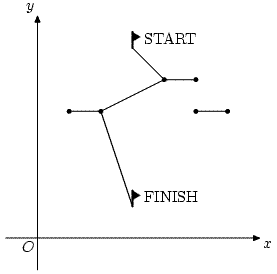
Маршрут должен представлять собой ломаную, начинающуюся в точке старта на вершине горы и заканчивающуюся в точке финиша у ее подножия. Маршрут выбирается таким образом, что y-координата каждой следующей вершины ломаной оказывается строго меньше y-координаты предыдущей вершины. Один из возможных маршрутов представлен на рисунке.
За каждые ворота, через которые не проходит маршрут, лыжнику начисляются штрафные очки. Общий штраф за спуск по маршруту вычисляется как сумма длины маршрута и штрафных очков за непройденные ворота.
Требуется написать программу, которая определяет, какой минимальный общий штраф горнолыжник может получить при прохождении трассы.
В первой строке входного файла задано число N - количество ворот на трассе (0 ≤ N ≤ 500), в следующих двух строках заданы Sx, Sy, Fx, Fy - координаты точек старта и финиша соответственно. В каждой из следующих N строк записаны четыре числа ai, bi, yi, ci - x-координаты левого и правого концов ворот, y-координата ворот и штраф за непрохождение данных ворот (ai < bi, Fy < yi < Sy, ci - целое число, 0 ≤ ci ≤ 10000). Все координаты - целые числа, не превосходящие по модулю 10000.
В выходной файл выведите наименьший возможный общий штраф за прохождение трассы с точностью не менее 4 знаков после десятичной точки.
Потестовая.
4 3 6 3 1 5 7 4 1 4 5 5 10 1 2 4 5 2 5 2 0
7.8126
Гомотетией с центром O и коэффициентом k 0 называют преобразование плоскости, при котором точка O переходит сама в себя, а любая точка X O – в такую точку Y, что:
Требуется написать программу, которая по координатам вершин двух различных простых N-угольников определяет, существует ли гомотетия, переводящая первый многоугольник во второй и, если существует, вычисляет ее центр и коэффициент.
В первой строке входного файла содержится целое число n (3 ≤ n ≤ 1000) – количество вершин в каждом многоугольнике
В следующих n строках – по два целых числа x и y (-106 ≤ x,y ≤ 106) – координаты вершин первого многоугольника в порядке обхода против часовой стрелки.
В следующих n строках – по два целых числа x и y (-106 ≤ x,y ≤ 106) – координаты вершин второго многоугольника в порядке обхода против часовой стрелки.
Если существует гомотетия, которая переводит первый многоугольник во второй, то необходимо вывести в первой строке выходного файла слово «YES», а во второй строке – три вещественных числа – координаты центра гомотетии и ее коэффициент, которые вычисляются с точностью не менее 10-5. Если искомой гомотетии не существует, необходимо вывести в выходной файл слово «NO».
3 -1 1 1 1 1 5 1 9 -3 1 1 1
YES 1.0 1.0 2.0
3 -1 1 1 1 1 5 1 1 0 0 1 0
NO
Движением плоскости называют такое преобразование плоскости, которое сохраняет попарные расстояния между точками, то есть если A1 и B1 – образы некоторых точек A и B при движении, то |A1B1| = |AB|.
Одной из разновидностей движения плоскости является скользящая симметрия. Скользящей симметрией называют композицию симметрии относительно некоторой прямой l и переноса на вектор, параллельный l (этот вектор может быть нулевым). На рисунке показан пример применения скользящей симметрии к отрезку.
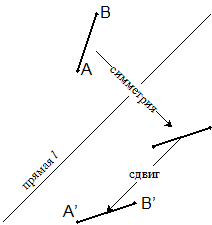
Известно, что любой отрезок можно перевести в любой другой отрезок такой же длины с помощью скользящей симметрии.
Требуется по координатам двух различных точек A и B и двух точек A1 и B1, находящихся на таком же расстоянии друг от друга, как и точки A и B, найти скользящую симметрию, переводящую точку A в точку A1, а точку B в точку B1.
В первой строке входного файла находятся четыре целых числа – координаты двух различных точек A и В. Во второй строке также находятся четыре целых числа – координаты двух различных точек A1 и В1. Гарантируется, что |A1B1| = |AB|. Все числа во входном файле по модулю не превышают 1000. Числа в строках разделены пробелом.
Выведите в выходной файл описание искомой скользящей симметрии, которое представляется в следующем виде.
В первой строке должны выводиться координаты двух различных точек, лежащих на прямой l, относительно которой выполняется симметрия, а во второй – координаты вектора, параллельного этой прямой, на который осуществляется перенос. Вещественные числа должны быть представлены не менее чем с 6 знаками после десятичной точки.
1 1 3 2 -1 1 -3 2
0.000000 0.000000 0.000000 1.000000 0.000000 0.000000
1 1 3 1 3 -1 5 -1
0.000000 0.000000 1.000000 0.000000 2.000000 0.000000