|
Максимальное время работы на одном тесте: |
2 секунды |
|
Максимальный объем используемой памяти: |
64 мегабайта |
На плоскости дано множество отрезков. Требуется найти прямую, которая пересекла бы наибольшее возможное количество из данных отрезков и при этом проходила бы как минимум через две точки с целочисленными координатами.
Считается, что прямая пересекает отрезок, если она имеет с ним хотя бы одну общую точку (т.е. она может проходить через конец отрезка, внутреннюю точку отрезка, либо содержать весь отрезок).
Формат входных данных
Сначала вводится число N — количество отрезков (1≤N≤1000). Далее идет N четверок чисел Xi1, Yi1, Xi2, Yi2 задающих координаты концов отрезков. Все эти числа целые, по модулю не превосходящие 10000.
Заданные отрезки могут пересекаться, иметь общие части, один из них может полностью содержаться внутри другого. Отрезки имеют ненулевую длину.
Формат выходных данных
Выведите координаты каких-нибудь двух точек, через которые проходит прямая, пересекающая наибольшее количество отрезков. Координаты точек должны быть целыми и не должны по модулю превышать 107.
Примеры
|
Входные данные |
Выходные данные |
Пояснение (кол-во отрезков, пересекаемых прямой) |
|
3 |
0 -1 1 4 |
3 |
|
2 |
0 0 1 0 |
2 |
|
2 |
1 0 1 1 |
2 |
|
5 |
10 3 1 4 |
4 |
В ежегодном чемпионате Флатландии (которая, естественно, является плоским миром) по космическим гонкам "Формула-3" участвуют N космических скутеров, имеющие форму треугольников. До начала гонок скутеры занимают положение в стартовой зоне согласно результатам жеребьевки.
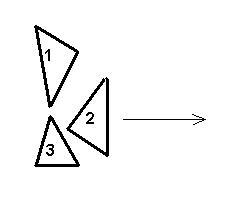
Скутеры стартуют строго по порядку. Каждый скутер,получив команду «старт», уезжает в положительном направлении оси Ox. Следующий скутер стартует лишь тогда, когда предыдущий покинет стартовую зону. Скутеры уезжают строго параллельно оси Ox, скутеры в стартовой зоне не поворачивают и не разворачиваются.
Естественно, что если в момент старта на пути скутера окажется другой скутер, то произойдет авария (даже если скутер заденет лишь угол другого скутера своим углом).
Для уменьшения опасности столкновения скутеров на старте строго соблюдается следующее правило: прямые, параллельные оси Ox и пересекающие какой-то скутер, должны в совокупности пересекать не более 100 других скутеров (прямая, проходящая через одну точку скутера также считается прямой, пересекающей скутер). Например, на приведенном рисунке прямые, параллельные Ox и пересекающие скутер 2, проходят через 2 других скутера (1 и 3), а прямые, проходящие через скутер 1, проходят только через один другой скутер (номер 2).
Главный Судья гонок хочет определить порядок, в котором должны стартовать скутеры, чтобы аварии не произошло. Например, в ситуации, приведенной на рисунке, сначала должен стартовать скутер номер 2 (если попытается стартовать скутер номер 1 или 3, то он столкнется со скутером номер 2). После этого скутеры 1 и 3 могут стартовать в любом порядке (они друг другу не мешают).
Помогите Главному Судье — напишите программу, которая определит какой-нибудь порядок старта скутеров, чтобы аварии не произошло.
В первой строке вводится натуральное число
В каждой из следующих N строк содержится по 6 чисел: x1, y1, x2, y2, x3, y3 – координаты трех вершин скутера на старте, целые числа, не превосходящие по модулю 106. В начальный момент скутеры не задевают друг друга.
Выведите через пробел N чисел – номера скутеров в том порядке, в котором они могут стартовать. Если решений несколько, выведите одно любое из них. Если решений нет, выведите одно число -1.
Примечание: первый тест соответствует приведенному рисунку. Ответ 2 3 1 в этом тесте также является правильным
3 1 19 3 9 6 15 5 6 10 2 10 12 1 1 6 1 3 7
3 0 1 -2 1 -1 -1 5 6 10 2 10 12 1 1 6 1 3 7
Петя и Вася играют в "точки". Петя отметил на клетчатом листе бумаги несколько точек – узлов сетки. Вася хочет окружить их многоугольником так, чтобы все отмеченные узлы лежали строго внутри (не на границе) этого многоугольника и чтобы все стороны этого многоугольника проходили только по сторонам или диагоналям клеток сетки, а его периметр был минимально возможным. Определите, чему равен периметр такого многоугольника.
В первой строке входных данных содержится число N – количество отмеченных Петей точек (1 ≤ N ≤ 100 000).
В каждой из следующих N строк записаны по два числа xi, yi – координаты точек, нарисованных Петей. Координаты по абсолютной величине не превосходят 106. Некоторые точки могут совпадать.
Требуется вывести одно число – периметр искомого многоугольника. Ответ нужно вывести с точностью не менее 0.001.
1 0 0
5.6568542495
2 1 1 1 2
7.6568542495
N вражеских кораблей движутся прямолинейно с постоянными скоростями. Вакуумная бомба уничтожает все объекты в радиусе R от точки взрыва (то есть все объекты, расстояние от которых до точки взрыва не больше R). Взрывать бомбу можно только в целые моменты времени.
Требуется определить, за какое наименьшее количество взрывов можно уничтожить все корабли, а также в какие моменты времени и в каких точках для этого следует произвести взрывы. Время отсчитывается от момента, когда координаты движущихся кораблей были определены со спутника.
В первой строке входных данных задаются целые числа N (2 <= N <= 10) и R (0 < R ≤ 50. В следующих Nстроках содержится по 4 числа, описывающих движение кораблей. Первые два числа строки – координаты корабля в момент времени 0, по модулю не превосходящие 105. Следующие два числа – значения координат вектора скорости, по модулю не превосходящие 1000. Все эти числа целые.
Гарантируется, что никакие 2 корабля не имеют одинаковые векторы скорости.Однако вполне возможно, что в какой-то момент времени два корабля пройдут через одну точку.
В первой строке выведите одно число – минимальное количество взрывов K. В следующих K строках для каждого взрыва выведите по три числа: целое время взрыва и вещественные координаты взрыва, указанные с точностью не менее трех значащих цифр после точки. Разрешается производить взрывы как в разные, так и в один и тот же момент времени. Разрешается взрывы производить как в различных точках, так и в одной точке в разные моменты времени.
Если решений несколько, выведите любое из них.
Комментарий. Решения, верно работающие при N ≤ 3, будут набирать не менее 50 баллов.
3 3 -3 3 1 0 0 -6 0 2 -8 6 4 -1
1 3 2.000 1.500
2 1 -4 -4 2 2 2 2 -2 -2
2 0 -4.0000 -4.0000 0 2.0000 2.0000
На плоскости задано N векторов. Есть 3 правила:
1) вектора на непересекающихся прямых можно сложить
2) вектора на одной прямой можно сложить (результат исходит из начала одного из векторов)
3) в любой точке можно породить два одинаковых по длине, но разнонаправленных вектора
Требуется найти эквивалентную данной систему, содержащую минимальное количество векторов.
На плоскости задано N векторов – направленных отрезков, для каждого из которых известны координаты начала и конца (вектор, у которого начало и конец совпадают, называется нуль-вектором, можно считать, что нуль-вектор лежит на любой прямой, которая через него проходит). Введем следующие три операции над направленными отрезками на плоскости:
1) Направленные отрезки ненулевой длины, лежащие на пересекающихся прямых, можно заменить на их сумму, причем единственным образом. В этом случае отрезки переносятся вдоль своих прямых так, чтобы их начала совпадали с точкой пересечения прямых, и складываются по правилу сложения векторов (правилу параллелограмма, при этом началом результирующего вектора является точка пересечения прямых).
2) Направленные отрезки, лежащие на одной прямой, также можно заменить на их сумму. Для этого один из отрезков (любой) нужно перенести в начало второго из них и сложить по правилу сложения векторов на прямой:
Это правило применимо и в случае, когда один из векторов, или даже оба, являются нуль-векторами.
Заметим, что если складываемые векторы противоположно направлены и имеют одну и ту же длину, то результатом их сложения является нуль вектор.
3) В любой точке плоскости можно породить два противоположно направленных отрезка равной (в том числе и нулевой) длины:
Будем говорить, что две системы векторов эквивалентны, если от одной системы можно перейти к другой с помощью конечной последовательности перечисленных выше операций.
Требуется получить любую систему векторов, эквивалентную заданной, состоящую из как можно меньшего числа векторов.
В первой строке входного файла записано число N – количество заданных векторов (1 < N ≤ 1000). В каждой из следующих N строк через пробел записаны четыре числа, обозначающие координаты начала и конца каждого из векторов соответственно. Все координаты – целые числа, по модулю не превосходящие 1000.
В первой строке входного файла следует записать число M – количество векторов в полученной системе (1 ≤ M ≤ N). В каждой из следующих M строк через пробел должны находиться четыре числа, обозначающие координаты начала и конца каждого из векторов соответственно. Все координаты – вещественные числа, записанные с 6 цифрами после точки.
3 1 1 1 3 3 3 3 1 5 1 7 1
1 3.000000 3.000000 5.000000 3.000000
2 2 4 5 10 -2 -4 -5 -10
1 2.000000 4.000000 2.000000 4.000000