#574

Выпуклая оболочка

Темы: [Многоугольники. Выпуклые оболочки] [Сканирующая прямая]

Источники: [ Командные олимпиады, ВКОШП, 2007, Задача C ]

На плоскости заданы углы (фигура, образованная лучами, исходящими из одной точки). Требуется найти "выпуклую оболочку", которая также ограничена двумя лучами.

Множество на плоскости называется выпуклым, если вместе с любыми двумя точками оно содержит также и отрезок, соединяющий эти точки. Минимальное по включению выпуклое множество, содержащее заданное множество точек \(X\), называется выпуклой оболочкой множества \(X\).

В этой задаче вам требуется найти выпуклую оболочку множества точек, принадлежащих заданному набору углов.

Углом называется геометрическая фигура, образованная двумя лучами, выходящими из одной точки. Эта точка называется вершиной угла.

На рисунке слева приведены два угла, на рисунке справа изображена их выпуклая оболочка.

Входные данные

В первой строке вводится число \(n\) - количество углов (1 <= \(n\) <= 1000). Каждая из следующих n строк содержит описание одного угла. Угол задается координатами трех точек: вершины и двух отличных от вершины точек - по одной на каждом из лучей. Все координаты целые и не превышают \(10^4\) по абсолютной величине. Величина угла находится в диапазоне от 0 до 180 градусов, не включительно.

Выходные данные

Выведите границу выпуклой оболочки в виде последовательности направленных лучей, прямых и отрезков. Никакие два объекта в выходных данных не должны лежать на одной прямой. Все отрезки должны иметь длину больше нуля. Объекты должны быть перечислены в таком порядке, чтобы начало каждого следующего совпадало с концом предыдущего. Все выводимые числа должны быть целыми и не превосходить \(10^5\) по абсолютной величине. При проходе вдоль описанной границы выпуклая оболочка углов должна быть справа. На первой строке выведите \(L\) - количество объектов в ответе. Следующие \(L\) строк должны содержать описание объектов. Объекты описываются следующим образом:

*Отрезок: "segment \(x_1\) \(y_1\) \(x_2\) \(y_2\)", где (\(x_1\), \(y_1\)) и (\(x_2\), \(y_2\)) - концы отрезка, отрезок считается направленным от (\(x_1\), \(y_1\)) к (\(x_2\), \(y_2\)).
*Луч, направленный от начала: "outray \(x_1\) \(y_1\) \(x_2\) \(y_2\)", где (\(x_1\), \(y_1\)) - начало луча, а (\(x_2\), \(y_2\)) - произвольная точка на луче, отличная от начала.
*Луч, направленный к началу: "inray \(x_1\) \(y_1\) \(x_2\) \(y_2\)", где (\(x_2\), \(y_2\)) - начало луча, а (\(x_1\), \(y_1\)) - произвольная точка на луче, отличная от начала.
*Прямая: "line \(x_1\) \(y_1\) \(x_2\) \(y_2\)", где (\(x_1\), \(y_1\)) и (\(x_2\), \(y_2\)) - две точки на прямой, причем при движении вдоль прямой в ее направлении точка (\(x_1\), \(y_1\)) следует ранее точки (\(x_2\), \(y_2\)).
*Если выпуклой оболочкой является вся плоскость, то выведите \(L\) = 0.

Примеры

Входные данные

2
3 1 4 1 4 4
2 2 4 3 3 4

Выходные данные

3
inray 4 1 3 1
segment 3 1 2 2
outray 2 2 3 5

Входные данные

2
0 0 1 0 0 1
0 0 -1 0 0 1

Выходные данные

1
line 0 0 -1 0

Входные данные

2
0 0 1 0 0 1
0 0 -1 0 0 -1

Выходные данные

#1134

РЛС

Темы: [Разбиения] [Многоугольники. Выпуклые оболочки]

Источники: [ Командные олимпиады, Кировские командные турниры, 2001, Задача G ]

Задана карта района, на которой присутствуют не более 5 связных фигур из клеток. Необходимо окружить все клетки забором минимальной длины (при этом группы клеток можно окружать отдельным забором).

Задачи противовоздушной обороны: ...борьба с десантом на всем маршруте пролета,

уничтожение вертолетов огневой поддержки, действующих из засады»

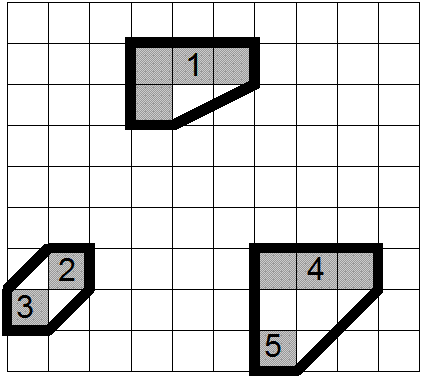Радиолокационная станция (РЛС) состоит из нескольких передатчиков (не более 5). К сожалению, их нельзя ставить рядом — они друг для друга создают помехи. Каждый передатчик состоит из квадратных модулей, которые располагаются вплотную друг к другу.

Вам дана карта района, в котором расположена РЛС. Вся карта для удобства разбита на квадраты, и для каждого квадрата известно, располагается в нем какой-то из модулей одного из передатчиков РЛС или нет.

Требуется оградить забором (или несколькими заборами) минимально возможной суммарной длины все передатчики РЛС. Забор — это произвольная ломаная (ее элементы не обязаны идти по сторонам клеток). Одним забором могут быть огорожены сразу несколько передатчиков.

Входные данные

Во входном файле записаны два числа N и M, задающие размеры района, в котором расположена РЛС (1N20, 1M20). Далее идет N строк, по M чисел в каждой, задающих карту района. Каждое из этих чисел 0 или 1 — 1 означает, что в этом квадрате находится один из модулей передатчика РЛС, а 0 — что в этом квадрате ничего ценного нет.

Общее количество передатчиков РЛС не превышает 5. Каждый передатчик — это связанная группа модулей (модули называются связанными, если они располагаются в квадратах карты, у которых есть общая граница, либо связаны через какие-то другие модули).

Ограничения на число модулей нет.

Выходные данные

В выходной файл выведите одно число — минимально возможную длину забора с тремя значащими цифрами после точки.

Примеры

Входные данные

2 2
1 0
0 1

Выходные данные

6.828

Входные данные

Выходные данные

18.000

#1757

Дракон Лун-Ян

Темы: [Сортировка слиянием] [Многоугольники. Выпуклые оболочки]

Источники: [ Командные олимпиады, Командные чемпионаты школьников Санкт-Петербурга по программированию, 2003, Задача F ]

Задан выпуклый многоугольник, составленный из проволоки. Требуется найти количество устойчивых положений многоугольника (когда он опирается на ось X двумя точками и центр масс многоугольника находится между ними)

Петя и его друг Андрейка только что познакомились с китайской мифологией. Особенно им понравились драконы. Поэтому мальчики решили сделать своих драконов из проволоки. Андрейка взял белую проволоку и согнул из неё дракона Лун-Инь: этот дракон спал, свернувшись клубком на столе. Тогда Петя взял чёрную проволоку и согнул дракона Лун-Ян. Этот дракон ничем не походил на Андрейкиного Лун-Иня. Его тело состояло из отрезков прямых, а когда он спал, то сворачивался в виде плоской замкнутой несамопересекающейся ломаной. Более того, Лун-Ян не ложился плашмя на стол для сна, а вставал перпендикулярно поверхности. Удержать равновесие дракон может только тогда, когда существуют две его различные точки, касающиеся стола, такие что центр масс дракона находится строго между ними.

Вам требуется узнать, сколько было устойчивых положений у дракона, в которых он мог сохранять равновесие во время сна, если известно, что форма ломаной в виде которой дракон спит всегда одна и та же.

Входные данные

В первой строке входного файла содержится число \(n\) (3 ≤ \(n\) ≤ 1000) – количество вершин ломаной и два целых числа \(x_c\) и \(y_c\) – координаты центра масс дракона (-1000 ≤ \(x_c\), \(y_c\) ≤ 1000). В следующих \(n\) строках содержится по два целых числа \(x_i\) и \(y_i\) (-1000 ≤ \(x_i\), \(y_i\) ≤ 1000) – координаты вершин ломаной в порядке обхода против часовой стрелки (ось \(O_X\) направлена вправо, а ось \(O_Y\) – вверх).

Выходные данные

В первой строке выходного файла выведите число устойчивых положений дракона.

Примеры

Входные данные

Выходные данные