Темы --> Информатика --> Язык программирования --> Массивы --> Двумерные массивы
---> 2 задач <---
Источники --> Личные олимпиады --> Нижегородская олимпиада школьников
    2009(6 задач)
    2010(6 задач)
    2011(6 задач)
    2012(6 задач)
    2013(6 задач)
    XI Нижегородская городская олимпиада по информатике им. В. Д. Лелюха, 2015г.(6 задач)
    XII Городская олимпиада школьников по информатике им. В. Д. Лелюха, 2016 г.(6 задач)
Страница: 1 Отображать по:
#3890
Шарики
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
256 megabytes

Фирма, в которой работает ваш друг, решила установить на конечной остановке своих маршруток большую абстрактную скульптуру со своим логотипом. Скульптура будет представлять собой прямоугольную сетку из \(N\) строк и \(M\) столбцов, в некоторых узлах которой будут располагаться разноцветные шары. Для обеспечения жёсткости конструкции шары, расположенные в узлах, соседних по вертикали, горизонтали или диагонали, необходимо соединить металлическими стержнями. Более строго, два шара должны быть соединены стержнем, если разность номеров строк, в которых расположены эти шары, не превосходит по модулю единицы, и разность номеров столбцов тоже не превосходит по модулю единицы.

Напишите программу, которая по заданному расположению шаров позволит определить, как будет выглядеть скульптура после установки стержней.

Входные данные

В первой строке входного файла находятся два натуральных числа \(N\) и \(M\) — размеры конструкции (\(1\leq N,M\leq 100\)). Далее следуют \(N\) строк по \(M\) символов в каждой. Каждый символ — это или “#” (решетка), обозначающий, что в соответствующем узле будет находиться шарик, или “.” (точка), обозначающий, что соответствующий узел будет пустой.

Выходные данные

Выведите в выходной файл \(2N-1\) строку по \(2M-1\) символов в каждой, изображающие как сами шары, так и соединяющие их стержни. А именно, в нечётных позициях нечётных строк выведите символ “#” или “.”, в зависимости от того, заполнен этот узел шариком или нет, а в остальных позициях выведите один из символов “ ” (пробел), “-” (минус), “|” (вертикальная палочка, ASCII #124), “/” (дробь, ASCII #47), “\” (обратный слеш, ASCII #92) или “X” (латинская заглавная буква X, ASCII #88), отражающий конфигурацию стержней в соответствующем месте структуры.

Если какая-то строка выходного файла должна заканчиваться на пробелы, их можно не выводить.

Примечание

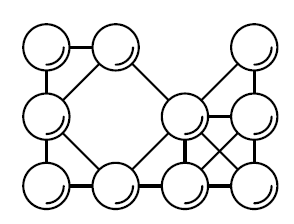
Первый пример соответствует рисунку.

Примеры
Входные данные
3 4
##.#
#.##
####
Выходные данные
#-# . #
|/ \ /|
# . #-#
|\ /|X|
#-#-#-#
Входные данные
3 4
.#..
#.#.
.#..
Выходные данные
. # . .
/ \
# . # .
\ /
. # . .
#3893
Переливание духов
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
256 megabytes

... но нужен ли на самом деле кому-нибудь 6\(1\over7\)-пунктовый шрифт, который на три четверти — шрифт Baskerville, и на четверть — Helvetica?

Дональд Э. Кнут. Идея Мета-фонта1

Маленькая девочка Оля добралась до полки, на которой стоят флаконы с мамиными любимыми духами, и начала заниматься своим любимым занятием — переливанием жидкостей из одного флакона в другой. Когда наконец мама застала её за этим занятием, прекрасная коллекция духов была уже безнадёжно утрачена.

К счастью, Оля — аккуратная девочка, поэтому все свои действия она записывала на бумажку. Помогите ей успокоить маму: определите, каков состав духов в первом (мамином любимом) флаконе, чтобы мама смогла придумать этой смеси новое название и рассказывать всем, какие прекрасные духи она смогла сделать вместе с дочерью.

Считайте, что Оля не пролила ни одной капли, а также что она тщательно встряхивала флаконы после каждого переливания. Учтите, что в маминых флаконах порой не видно, есть ли там жидкость, и потому Оля иногда могла пытаться переливать духи из пустого флакона (в результате, естественно, ничего не переливалось). Вы можете также считать, что после каждого переливания в каждом флаконе каждый тип духов либо полностью отсутствует, либо содержится в объеме не меньшем чем \(10^{-10}\).

Входные данные

На первой строке входного файла находятся два числа \(N\) и \(M\) — количество флаконов и число типов маминых любимых духов соответственно (\(2 \leq N \leq 100\); \(1 \leq M \leq 100\)). Далее следуют \(N\) строк, на \(i\)-ой из которых находятся два числа — тип \(L_i\) и объем \(V_i\) духов, находившихся изначально в \(i\)-ом флаконе (\(1\leq L_i \leq M\); \(0 \leq V_i \leq 1000\)). Возможно, что в нескольких флаконах находились духи одного и того же типа; возможно, что какого-то типа вообще не было на полке.

Далее во входном файле следует строка с числом \(K\) — количеством совершённых переливаний (\(1 \leq K \leq 1000\)). За ней следуют \(K\) строк, на \(k\)-ой из которых находятся три числа \(S_k\), \(T_k\) и \(A_k\) — номера флаконов, откуда и куда переливала Оля при \(k\)-ом переливании, и количество перелитой жидкости (в процентах от количества жидкости в \(S_k\)-ом флаконе перед переливанием). Гарантируется, что \(1\leq S_k,T_k\leq N\), что \(S_k\neq T_k\), и что \(0\leq A_k\leq 100\). Все числа во входном файле целые.

Выходные данные

В выходной файл выведите \(M\) чисел — процентное содержание всех видов духов (от первого до \(M\)-ого) в первом флаконе после последнего переливания. Выводите результат с точностью не меньше двух знаков после запятой. Гарантируется, что после последнего переливания первый флакон оказался непустым.

Примечание

1... but does anybody really need a 6\(1\over7\)-point font that is one fourth of the way between Baskerville and Helvetica? — Donald E. Knuth, The Concept of a Meta-Font

Примеры
Входные данные
3 2
1 100
2 200
1 500
2
3 2 20
2 1 50
Выходные данные
60.00 40.00
Страница: 1 Отображать по:
Выбрано
:
Отменить
|
Добавить в контест