Окружная олимпиада(18 задач)
Региональный этап(109 задач)
Заключительный этап(97 задач)
Известный математик Соломон В. Голомб предложил название полимино для связной фигуры, вырезанной из клетчатой бумаги по линиям сетки. Фигура называется связной, если из любой ее клетки можно добраться в любую другую, переходя из клетки в клетку через их общую сторону. Шахматист, добавил Голомб, сказал бы, что из любой клетки полимино можно дойти ладьей в любую другую. На рис. 1 приведены примеры восьми полимино.
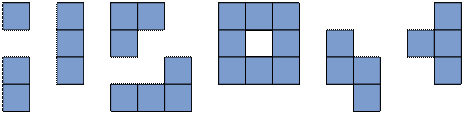
Рис. 1
Саша увлекается полимино. Для своих экспериментов она вырезает новое полимино из бумаги в клеточку или из старых полимино, оставшихся после предыдущих попыток. Далеко не всегда из старого полимино (рис. 2а, слева) можно вырезать новое (рис. 2а, справа). Поэтому Саша может перед вырезанием нового полимино разделить каждую клетку старого полимино на K2 одинаковых квадратных клеток меньшего размера (см. рис. 2б, здесь K = 2).
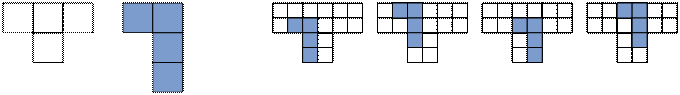
Рис. 2а Рис. 2б
Сашу заинтересовало, сколько существует различных способов вырезать новое полимино из старого при заданном значении K, если повороты, отражения и переворачивания как нового полимино, так и старого, недопустимы.
Например, на рис. 2б приведены все возможные способы вырезания полимино, приведенного на рис. 2а, при K = 2.
Напишите программу, которая ответит на интересующий Сашу вопрос.
Первая строка входных данных содержит число K (1 ≤ K ≤ 10 000).
Далее следуют описания двух полимино, сначала нового, затем старого. Каждое полимино задается следующим образом — в первой строке описания задаются размеры H (высота) и W (ширина) минимально возможного прямоугольника, в котором можно разместить данное полимино. Следующие Н строк содержат по W символов описания клеток. При этом клетка, входящая в полимино, обозначается символом « X» (прописная латинская буква «икс»), а не входящая — символом «.» (точка). Количество клеток в каждом полимино не превышает 300.
Выведите одно число — количество различных способов вырезать заданное новое полимино из старого, каждая клетка которого разбита на K2 клеток.
2 6 6 XXXXXX X....X X....X X....X X....X XXXXXX 5 5 XXXXX XXXXX XX.XX XXXXX XXXXX
9
Для проведения олимпиады школьников по информатике требуется соединить компьютеры в сеть. Организаторы олимпиады разработали схему соединения компьютеров. В соответствии с этой схемой некоторые пары компьютеров должны быть соединены кабелем, и сигнал сможет дойти по кабелям от любого компьютера до любого другого, возможно, через другие компьютеры.
Некоторые компьютеры могут быть соединены циклически. Цикл называется простым, если каждый компьютер из этого цикла соединён ровно с двумя другими компьютерами этого цикла, и в этот цикл никакой кабель не входит более одного раза. Некоторые кабели могут не входить ни в какой цикл.
Известно, что в разработанной схеме никакой кабель не принадлежит двум простым циклам одновременно.
Организаторам олимпиады поручено разместить компьютеры в зале соревнований. При размещении должны выполняться следующие условия:
1.Компьютеры размещаются на плоскости в точках с целочисленными координатами.
2.Координаты компьютеров x и y лежат в диапазоне 0 ≤ x, y ≤ 106.
3.Никакие два компьютера не располагаются в одной точке.
4.Кабели являются отрезками прямых.
5.Кабели не пересекаются между собой и не проходят через точки размещения компьютеров, к которым они не подключены.
Требуется написать программу, выполняющую размещение компьютеров по заданному описанию схемы.
В первой строке входного файла содержатся числа N и M — количество компьютеров и количество кабелей в схеме (1 ≤ N ≤ 100 000, 0 ≤ M ≤ 200 000). В последующих M строках содержатся пары чисел, разделенных пробелами. Каждая такая пара описывает один кабель, числа представляют собой номера соединенных компьютеров. Компьютеры пронумерованы от 1 до N. Никакая пара не встречается дважды, и никакой кабель не соединяет компьютер с самим собой.
Выходной файл должен содержать N строк. Строка с номером i должна содержать координаты i-го компьютера, разделенные пробелом. Сначала выводится координата x, затем y. Разрешается вывести любой вариант размещения компьютеров, при котором выполняются условия 1–5.
Примечания
Пример входных и выходных данных
|
Ввод |
Вывод |
|
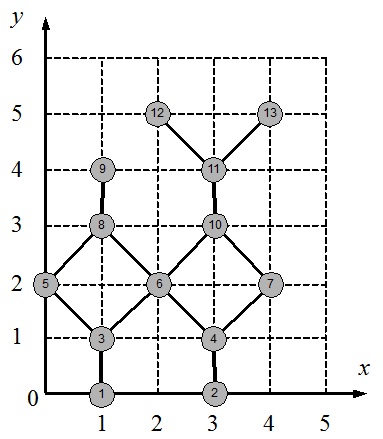
13 14 11 12 11 13 1 3 3 5 5 8 8 9 8 6 6 3 4 6 4 2 6 10 10 11 10 7 7 4 |
1 0 3 0 1 1 3 1 0 2 2 2 4 2 1 3 1 4 3 3 3 4 2 5 4 5 |
Недавно на уроке информатики ученики одного из классов изучили булевы функции. Напомним, что булева функция \(f\) сопоставляет значениям двух булевых аргументов, каждый из которых может быть равен 0 или 1, третье булево значение, называемое результатом. Для учеников, которые выразили желание более подробно изучать эту тему, учительница информатики на дополнительном уроке ввела в рассмотрение понятие цепного вычисления булевой функции \(f\).
Если задана булева функция \(f\) и набор из \(N\) булевых значений \(a_1,a_2,\ldots,a_N\), то результат цепного вычисления этой булевой функции определяется следующим образом:
* если \(N=1\), то он равен \(a_1\);
* если \(N>1\), то он равен результату цепного вычисления булевой функции \(f\) для набора из \((N-1)\) булевого значения \(f(a_1,a_2),a_3,\ldots,a_N\), который получается путём замены первых двух булевых значений в наборе из \(N\) булевых значений на единственное булево значение — результат вычисления функции \(f\) от \(a_1\) и \(a_2\).
Например, если изначально задано три булевых значения: \(a_1=0\), \(a_2=1\), \(a_3=0\), а функция \(f\) — ИЛИ (OR), то после первого шага получается два булевых значения — (0 OR 1) и 0, то есть 1 и 0. После второго (и последнего) шага получается результат цепного вычисления, равный 1, так как 1 OR 0 = 1.
В конце дополнительного урока учительница информатики написала на доске булеву функцию \(f\) и попросила одного из учеников выбрать такие \(N\) булевых значений \(a_i\), чтобы результат цепного вычисления этой функции был равен единице. Более того, она попросила найти такой набор булевых значений, в котором число единиц было бы как можно бо́льшим.
Требуется написать программу, которая решала бы поставленную учительницей задачу.
Первая строка входного файла содержит одно натуральное число \(N\) (\(2\le N\le100\,000\)).
Вторая строка входного файла содержит описание булевой функции в виде четырёх чисел, каждое из которых — ноль или единица. Первое из них есть результат вычисления функции в случае, если оба аргумента — нули, второе — результат в случае, если первый аргумент — ноль, второй — единица, третье — результат в случае, если первый аргумент — единица, второй — ноль, а четвёртый — в случае, если оба аргумента — единицы.
В выходной файл необходимо вывести строку из \(N\) символов, определяющих искомый набор булевых \(a_i\) с максимально возможным числом единиц. Если ответов несколько, требуется вывести любой из них. Если такого набора не существует, выведите в выходной файл фразу «No solution».
В первом примере процесс вычисления цепного значения булевой функции \(f\) происходит следующим образом: \(1011\to111\to01\to1\)
Во втором примере вычисление цепного значения булевой функции \(f\) происходит следующим образом: \(11111\to0111\to111\to01\to1\)
В третьем примере получить цепное значение булевой функции \(f\), равное 1, невозможно.
4 0110
1011
5 0100
11111
6 0000
No solution