Темы
    Информатика(2656 задач)
---> 304 задач <---
Источники --> Личные олимпиады --> Всероссийская олимпиада школьников
    Муниципальный этап(80 задач)
    Окружная олимпиада(18 задач)
    Региональный этап(109 задач)
    Заключительный этап(97 задач)
Страница: << 29 30 31 32 33 34 35 >> Отображать по:
#3817
Поле для игры
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

Петя создает поле для своей новой игры. Поле разделено на клетки и представляет собой прямоугольник размером N на M клеток. Пусть клетки имеют координаты от 1 до N слева направо по горизонтали и от 1 до M снизу вверх по вертикали.

На этом поле Петя уже разместил супермаркет, который представляет собой прямоугольник размером C на D клеток (C –– размер по горизонтали, D –– по вертикали), и нижняя левая клетка супермаркета имеет координаты A, B на игровом поле (см. примеры и рисунки). Теперь Пете нужно разместить на том же игровом поле здание биржи. Здание биржи представляет собой прямоугольник размером E на F клеток (E –– по горизонтали, F –– по вертикали). Естественно, что здание биржи должно полностью располагаться на игровом поле и не должно иметь общих клеток с супермаркетом (но может касаться его).

Сколькими способами Петя сможет разместить здание биржи?

Входные данные

Вводятся числа N, M, A, B, C, D, E, F, каждое в отдельной строке. Числа удовлетворяют следующим условиям: 1 ≤ N ≤ 100, 1 ≤ M ≤ 100, 1 ≤ A ≤ N, 1 ≤ B ≤ M, 1 ≤ A + C - 1 ≤ N, 1 ≤ B + D - 1 ≤ M, 1 ≤ E ≤ N, 1 ≤ F ≤ M.

Выходные данные

Выведите количество способов разместить здание биржи.

Примеры тестов

Входные данные
6
5
2
3
3
2
1
2
Выходные данные
15
Входные данные
4
4
2
2
3
2
2
2
Выходные данные
0
Входные данные
6
5
1
1
3
3
3
3
Выходные данные
3

Примечание

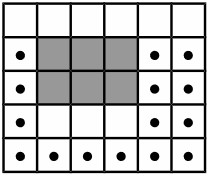
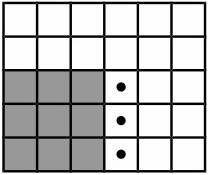
Рисунки ниже соответствуют приведенным примерам. На рисунках серым показано здание супермаркета. Точками отмечены варианты размещения нижнего левого угла здания биржи.

#3818
Дома и магазины
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

На Новом проспекте построили подряд 10 зданий. Каждое здание может быть либо жилым домом, либо магазином, либо офисным зданием.

Но оказалось, что жителям некоторых домов на Новом проспекте слишком далеко приходится идти до ближайшего магазина. Для разработки плана развития общественного транспорта на Новом проспекте мэр города попросил вас выяснить, какое же наибольшее расстояние приходится преодолевать жителям Нового проспекта, чтобы дойти от своего дома до ближайшего магазина.

Входные данные

Программа получает на вход десять чисел, разделенных пробелами. Каждое число задает тип здания на Новом проспекте: число 1 обозначает жилой дом, число 2 обозначает магазин, число 0 обозначает офисное здание. Гарантируется, что на Новом проспекте есть хотя бы один жилой дом и хотя бы один магазин.

Выходные данные

Выведите одно целое число: наибольшее расстояние от дома до ближайшего к нему магазина. Расстояние между двумя соседними домами считается равным 1 (то есть если два дома стоят рядом, то между ними расстояние 1, если между двумя домами есть еще один дом, то расстояние между ними равно 2 и т.д.)

Примеры тестов

Входные данные
2 0 1 1 0 1 0 2 1 2
Выходные данные
3

Примечание

В примере из условия дальше всего идти до ближайшего магазина жителям четвертого дома: ближайший к их дому магазин находится в первом доме, и им нужно пройти три дома до него. Жителям других домов придется пройти меньшее расстояние до ближайшего магазина, поэтому ответ 3.

#3819
Маска файла
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

Миша готовится к ЕГЭ по информатике. Сейчас он изучает задачу A4, в которой описывается работа с масками файлов:

Для групповых операций с файлами используются маски имён файлов. Маска представляет собой последовательность букв, цифр и прочих допустимых в именах файлов символов, в которой также могут встречаться следующие символы.

Символ «?» (вопросительный знак) означает ровно один произвольный символ.

Символ «*» (звёздочка) означает любую последовательность символов произвольной длины, в том числе «*» может задавать и пустую последовательность.

Поскольку открытого банка задач для ЕГЭ по информатике не существует, Мише приходится тренироваться самостоятельно. Напишите программу, которая для каждого имени файла определит, подходит ли оно под заданную маску, чтобы Миша мог сверить свои ответы. Гарантируется, что в маске файла присутствует не более одного символа «*».

Входные данные

В первой строке содержится маска файла. В следующих 5 строках содержатся имена файлов по одному в строке. Имена файлов состоят из маленьких латинских букв, цифр и символа «.» (точка), в маске также могут содержаться символы «?» и «*» (символ «*» — не более одного раза). Длина каждой строки не превосходит 20 символов.

Выходные данные

Для каждого имени файла выведите слово «YES» если оно удовлетворяет маске и «NO» иначе. Выводить слова следует большими латинскими буквами без кавычек, каждое в новой строке.

Примеры тестов

Входные данные
?or*.d??
fort.doc
ford.doc
lord2.doc
orsk.dat
port
Выходные данные
YES
YES
YES
NO
NO

#3820
Распечатка условий
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

Популярность окружной олимпиады по информатике растет год от года. При этом организаторы должны заранее распечатать как условия задач, так и другие материалы олимпиады (анкеты, памятки и т.п). В этом году они оценили объем печатной продукции в N листов.

Фирма, готовая размножить печатные материалы, предлагает следующие финансовые условия. Один лист она печатает за A1 рублей, 10 листов — за A2 рублей, 100 листов — за A3 рублей, 1000 листов — за A4 рублей, 10 000 листов — за A5 рублей, 100 000 листов — за A6 рублей и 1 000 000 листов — за A7 рублей. При этом не гарантируется, что один лист в более крупном заказе обойдется дешевле, чем в более мелком. И даже может оказаться, что для любой партии будет выгодно воспользоваться тарифом для одного листа.

Печать конкретного заказа производится или путем комбинации нескольких тарифов, или путем заказа более крупной партии. Например, 980 листов можно распечатать, заказав печать 9 партий по 100 листов плюс 8 партий по 10 листов, сделав 98 заказов по 10 листов, 980 заказов по 1 листу или заказав печать 1000 (или даже 10 000 и более) листов, если это окажется выгоднее.

Требуется по заданному объему заказа в листах N определить минимальную сумму денег в рублях, которой будет достаточно для выполнения заказа.

Входные данные

На вход программе сначала подается число N (1 ≤ N ≤ 2 × 109) — количество листов в заказе. В следующих 7 строках ввода находятся натуральные числа A1, A2, A3, A4, A5, A6, A7 соответственно (1 ≤ Ai ≤ 106).

Выходные данные

Выведите одно число — минимальную сумму денег в рублях, которая нужна для выполнения заказа. Гарантируется, что правильный ответ не будет превышать 2 × 109.

Примеры тестов

Входные данные
980
1
9
90
900
1000
10000
10000
Выходные данные
882
Входные данные
980
1
10
100
1000
900
10000
10000
Выходные данные
900

#3854
Fruit Slice
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

Правила игры Fruit Slice для сенсорных мобильных телефонов очень просты. В течение некоторого времени на экране появляются фрукты, а игрок должен провести пальцем по экрану так, чтобы линии, проведенные им, пересекли как можно больше фруктов. В случае, если линия пересекает фрукт, он разрезается на две половинки, а игрок получает очки следующим образом:

  • за разрезание большого фрукта игрок получает два очка, за разрезание маленького — три;
  • если одной линией игрок разрезал три фрукта, то помимо очков, полученных за каждый фрукт по отдельности, он получает еще 5 бонусных очков;
  • если одной линией игрок разрезал 4 и более фруктов, то помимо очков, полученных за каждый фрукт по отдельности, он получает еще 10 бонусных очков.

Вася поиграл в игру и набрал суммарно P очков, при этом N раз получив 5 бонусных очков и M раз получив 10 бонусных очков. Теперь ему интересно, какое минимальное количество фруктов можно разрезать согласно правилам этой игры, чтобы добиться такого же результата.

Входные данные

В единственной строке вводятся три числа P, N и M (0 ≤ P ≤ 109, 0 ≤ N, M ≤ 106).

Выходные данные

Выведите одно число — минимальное количество фруктов, которое нужно разрезать, чтобы добиться указанного результата. Гарантируется, что входные данные корректны, то есть существует такой набор фруктов, что возможно набрать суммарно P очков, при этом N раз получив 5 бонусных очков и M раз получив 10 бонусных очков.

Примечание

В первом примере добиться указанного результата можно, разрезав 5 маленьких фруктов и 1 большой. При этом у игрока есть возможность получить 5 бонусных очков, разрезав какие-то три фрукта одной линией.

Во втором примере добиться указанного результата можно, разрезав одной линией 3 больших фрукта и 1 маленький. Обратите внимание, что поскольку Вася один раз получил 10 бонусных очков, он не может добиться указанного результата, разрезав менее 4-х фруктов.

Система оценки

Тесты в этой задаче разбиты на группы. Баллы начисляются только за группу целиком в том случае, когда пройдены все тесты группы, а также все тесты предыдущих групп.

  1. Тесты 1–2. Тесты из условия, оцениваются в 0 баллов.
  2. Тесты 3–5. \(P \le 30\), \(N, M \le 1\), оцениваются в 30 баллов.
  3. Тесты 6–9. \(P \le 10^7\), оцениваются в 30 баллов.
  4. Тесты 10–12. Дополнительных ограничений нет, оцениваются в 40 баллов.

Примеры
Входные данные
22 1 0
Выходные данные
6
Входные данные
19 0 1
Выходные данные
4
Страница: << 29 30 31 32 33 34 35 >> Отображать по:
Выбрано
:
Отменить
|
Добавить в контест