#601

Забор

Темы: [Формула]

Источники: [ Личные олимпиады, Всероссийская олимпиада школьников, Окружная олимпиада, 2007, 2 тур, Задача A ]

Том Сойер получил важное задание по покраске забора. Забор состоит из n досок. Он когда-то был покрашен, однако с некоторых участков забора краска облупилась. Эти доски Тому и необходимо покрасить. Так как забор большой, пришлось подвезти к забору целую цистерну с краской. Цистерна была помещена у края забора и не может перемещаться. У Тома есть ведерко, набрав краски в которое, Том может покрасить \(k\) досок забора. При этом Том может в любой момент вернуться за краской к цистерне.

Изначально Том находится у цистерны. Соседние доски находятся на расстоянии 1 фута друг от друга, цистерна находится на расстоянии 1 фута от первой доски. По окончании работы Том должен положить кисточку и ведерко на свою исходную позицию рядом с цистерной.

Требуется выяснить, какое минимальное расстояние Тому необходимо пройти, чтобы покрасить забор.

Входные данные

Первая строка входного файла содержит количество досок в заборе \(n\) (1 ≤ \(n\) ≤ \(10^9\)) и вместимость ведерка \(k\) (1 ≤ \(k\) ≤ 100). Во второй строке содержится количество неокрашенных отрезков забора \(m\) (1 ≤ \(m\) ≤ 50). Далее следуют \(m\) строк, в каждой из которых описан один неокрашенный отрезок. Отрезок описывается своей левой границей \(l_i\) и правой границей \(r_i\) (1 ≤ \(l_i\) ≤ \(r_i\) ≤ \(n\)). Такое описание означает, что не покрашены \(l_i\)-я, (\(l_i\)+1)-я, …, (\(r_i\)–1)-я, \(r_i\)-я доски забора (доски нумеруются от 1 до \(n\)). Гарантируется, что неокрашенные отрезки, заданные во входном файле, не пересекаются.

Выходные данные

Выведите одно число — минимальное расстояние в футах, которое необходимо пройти Тому для выполнения своего ответственного задания.

Примеры

Входные данные

Выходные данные

#720

Минимальное число

Темы: [Сортировка выбором (максимума)]

Источники: [ Личные олимпиады, Всероссийская олимпиада школьников, Муниципальный этап, Москва, 2007, Задача D ]

Дано натуральное четырехзначное число. Найдите минимальное натуральное четырехзначное число, состоящее из тех же цифр, что и заданное. Заметим, что четырехзначные числа не могут начинаться с нуля.

Входные данные

Вводится натуральное четырехзначное число.

Выходные данные

Выведите минимальное натуральное четырехзначное число, состоящее из тех же цифр.

Примеры

Входные данные

Выходные данные

#721

Шнурки

Темы: [Целые числа]

Источники: [ Личные олимпиады, Всероссийская олимпиада школьников, Муниципальный этап, Москва, 2007, Задача A ]

Обувная фабрика собирается начать выпуск элитной модели ботинок. Дырочки для шнуровки будут расположены в два ряда, расстояние между рядами равно a, а расстояние между дырочками в ряду b. Количество дырочек в каждом ряду равно N.

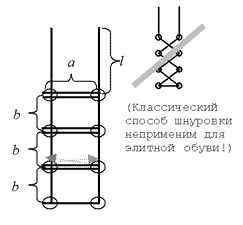Рис. 1 Шнуровка должна происходить элитным способом «наверх, по горизонтали в другой ряд, наверх, по горизонтали и т.д.» (см. рисунок). Кроме того, чтобы шнурки можно было завязать элитным бантиком, длина свободного конца шнурка должна быть l.

Какова должна быть длина шнурка для этих ботинок?

Входные данные

Вводятся четыре натуральных числа a, b, l и N.

Выходные данные

Ваша программа должна выводить одно число – искомую длину шнурка.

Примеры

Входные данные

2 1 3 4

Выходные данные

#722

Пересадки

Темы: [Пересечение множеств]

Источники: [ Личные олимпиады, Всероссийская олимпиада школьников, Муниципальный этап, Москва, 2007, Задача B ]

На Новом проспекте для разгрузки было решено пустить два новых автобусных маршрута на разных участках проспекта. Известны конечные остановки каждого из автобусов. Определите количество остановок, на которых можно пересесть с одного автобуса на другой.

Входные данные

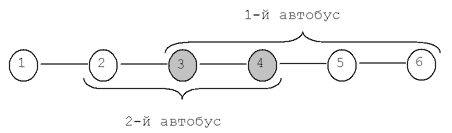
Вводятся четыре числа, не превосходящие 100, задающие номера конечных остановок. Сначала для первого, потом второго автобуса (см. примеры и рисунок).

Выходные данные

Ваша программа должна выводить одно число – искомое количество остановок.

Задача В, рис. 2

Пояснения

Первый пример (см. рисунок): первый автобус ходит с 3-й остановки по 6-ю и обратно, а второй с 2-й по 4-ю и обратно. Пересесть с одного автобуса на другой можно на 3-й и 4-й остановках. Их две.

Второй пример: автобусы не имеют общих остановок.

Примеры

Входные данные

3 6 4 2

Выходные данные

Входные данные

3 1 5 10

Выходные данные

#723

Метод бутерброда

Темы: [Строки]

Источники: [ Личные олимпиады, Всероссийская олимпиада школьников, Муниципальный этап, Москва, 2007, Задача C ]

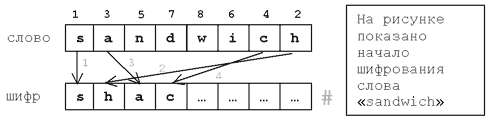
Секретное агентство «Super-Secret-no» решило для шифрования переписки своих сотрудников использовать «метод бутерброда». Сначала буквы слова нумеруются в таком порядке: первая буква получает номер 1, последняя буква - номер 2, вторая – номер 3, предпоследняя – номер 4, потом третья … и так для всех букв (см. рисунок). Затем все буквы записываются в шифр в порядке своих номеров. В конец зашифрованного слова добавляется знак «диез» (#), который нельзя использовать в сообщениях.

Например, слово «sandwich» зашифруется в «shacnidw#».

Задача С, рис. 3

К сожалению, программист «Super-Secret-no», написал только программу шифрования и уволился. И теперь агенты не могут понять, что же они написали друг другу. Помогите им.

Входные данные

Вводится слово, зашифрованное методом бутерброда. Длина слова не превышает 20 букв.

Выходные данные

Выведите расшифрованное слово.

Примеры

Входные данные

Aabrrbaacda#

Выходные данные

Abracadabra