Алгоритмы(1657 задач)
Структуры данных(279 задач)
Интерактивные задачи(17 задач)
Другое(54 задач)
Окружная олимпиада(18 задач)
Региональный этап(109 задач)
Заключительный этап(97 задач)
В непроходимом лесу имеется N полянок и M тропинок между ними. Каждая тропинка соединяет две различные полянки. Две полянки могут быть соединены несколькими тропинками.
На двух разных полянках живут Красная Шапочка и ее бабушка. Домик Красной Шапочки находится на полянке с номером 1, а домик бабушки - на полянке с номером N. Красная Шапочка хорошо ориентируется в лесу и знает, какое минимальное время ей потребуется для прохождения каждой тропинки. Когда Красная Шапочка идет по лесу, она переходит с тропинки на тропинку только на полянках. На каждой полянке есть укрытие, в котором Красная Шапочка может спрятаться на некоторое время.
В этом же лесу живет Волк. Время, за которое Волк пробегает какую-либо тропинку, может отличаться от времени, за которое по ней проходит Красная Шапочка. Кроме того, если Волк пробегает по одной и той же тропинке несколько раз, то каждый раз он может тратить на это разное время.
С края полянки, где живет Красная Шапочка, Волк увидел, что она собирается нести пирожки бабушке и побежал по тропинкам привычного ему пути от дома Красной Шапочки к дому бабушки. Волк начинает бежать от домика Красной Шапочки в тот момент, когда она решила выйти из дома, его путь заканчивается как только он окажется на полянке с домиком бабушки. Ни на одной полянке Волк не задерживается.
Чтобы застать бабушку в целости и сохранности, Красной Шапочке необходимо обогнать Волка. При этом ей нельзя оказаться с Волком на одной тропинке, даже если Волк уже покидает ее, а она только появляется на ней, или наоборот. Чтобы избежать встречи с Волком на полянке, Красная Шапочка использует имеющееся там укрытие. Красной Шапочке нельзя появляться на полянке одновременно с Волком или покидать укрытие на полянке в тот момент, когда на ней появляется Волк. При необходимости Красная Шапочка может идти по тропинке дольше минимально возможного времени, а также выйти из дома позже, чем она исходно решила.
Необходимо написать программу, которая поможет Красной Шапочке добраться к бабушке раньше Волка, если известна последовательность тропинок, по которым побежал Волк.
Первая строка входного файла содержит числа N, M и K (2 ≤ N ≤ 2000, 1 ≤ M ≤ 100000, 1 ≤ K ≤ 100000). Следующие M строк содержат по три числа: Bi, Ei - номера полянок, которые соединяет i-я тропинка, и Ti - минимальное время, за которое Красная Шапочка может по ней пройти (1 ≤ Ti ≤ 10000). В следующих K строках находится последовательное описание пути Волка, по два числа в строке: Pi - номер тропинки, по которой он побежит, и Vi - время, которое он на это затратит (1 ≤ Vi ≤ 10000). Путь волка всегда начинается на полянке 1 и заканчивается на полянке N. Все числа во входном файле целые и в пределах одной строки разделены пробелами.
В том случае, если Красная Шапочка не может добраться до домика бабушки быстрее Волка, выходной файл должен содержать слово 'NO'.
Если Красная Шапочка сможет добраться до домика бабушки быстрее волка, в первой строке выходного файла должно быть слово 'YES'. Во второй строке в этом случае должно содержаться число тропинок в пути Красной Шапочки. В третью строку следует вывести номера тропинок в том порядке, в котором Красная Шапочка должна по ним пройти. Числа должны быть разделены пробелами.
Информацию о времени прохождения по тропинкам и остановках на полянках в выходной файл выводить не нужно.
\(2 \leq N \leq 200\) Решение оценивается в \(30\) баллов.
\(NK \leq 6 \cdot 10^6\) Решение оценивается в \(40\) баллов.
Дополнительные ограничения отсутствуют. Решение оценивается в \(30\) баллов.
3 2 3 1 2 13 1 3 9 1 5 1 5 2 5
YES 1 2
Рассмотрим прямоугольную таблицу размером n m. Занумеруем строки таблицы числами от 1 до n, а столбцы – числами от 1 до m. Будем такую таблицу последовательно заполнять числами следующим образом.
Обозначим через aij число, стоящее на пересечении i-ой строки и j-ого столбца. Первая строка таблицы заполняется заданными числами – a11, a12, …, a1m. Затем заполняются строки с номерами от 2 до n. Число aij вычисляется как сумма всех чисел таблицы, находящихся в «треугольнике» над элементом aij. Все вычисления при этом выполняются по модулю r.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ai,j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Более точно, значение aij вычисляется по следующей формуле:
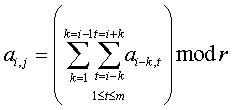
Например, если таблица состоит из трех строк и четырех столбцов, и первая строка состоит из чисел 2,3,4,5, а r = 40 то для этих исходных данных таблица будет выглядеть следующим образом (взятие по модулю показано только там, где оно приводит к изменению числа):
| 2 | 3 | 4 | 5 |
| 5 = 2 + 3 | 9 = 2 + 3 + 4 | 12 = 3 + 4 + 5 | 9 = 4 + 5 |
| 23 = 2 + 3 + 4 + 5 + 9 | 0 = (2 + 3 + 4 + 5 + 5 + 9 + 12) mod 40 = 40 mod 40 | 4 = (2 + 3 + 4 + 5 + 9 + 12 + 9) mod 40 = 44 mod 40 | 33 = 3 + 4 + 5 + 12 + 9 |
Требуется написать программу, которая по заданной первой строке таблицы (a11, a12, …, a1m), вычисляет последнюю строку, как описано выше.
Первая строка входного файла содержит числа n, m и r (2 ≤ n, m ≤ 2000, 2 ≤ r ≤ 109) – число строк и столбцов таблицы соответственно, а так же число, по модулю которого надо посчитать ответ. Следующая строка содержит m целых чисел – первую строку таблицы: a11, a12, …, a1m. Все a1i неотрицательны и не превосходят 109.
В первой строке выходного файла необходимо вывести m чисел – последнюю строку таблицы: an1, an2, …, anm.
2 3 10 1 2 3
3 6 5
3 3 10 1 1 1
8 0 8
3 4 40 2 3 4 5
23 0 4 33
Гомотетией с центром O и коэффициентом k 0 называют преобразование плоскости, при котором точка O переходит сама в себя, а любая точка X O – в такую точку Y, что:
Требуется написать программу, которая по координатам вершин двух различных простых N-угольников определяет, существует ли гомотетия, переводящая первый многоугольник во второй и, если существует, вычисляет ее центр и коэффициент.
В первой строке входного файла содержится целое число n (3 ≤ n ≤ 1000) – количество вершин в каждом многоугольнике
В следующих n строках – по два целых числа x и y (-106 ≤ x,y ≤ 106) – координаты вершин первого многоугольника в порядке обхода против часовой стрелки.
В следующих n строках – по два целых числа x и y (-106 ≤ x,y ≤ 106) – координаты вершин второго многоугольника в порядке обхода против часовой стрелки.
Если существует гомотетия, которая переводит первый многоугольник во второй, то необходимо вывести в первой строке выходного файла слово «YES», а во второй строке – три вещественных числа – координаты центра гомотетии и ее коэффициент, которые вычисляются с точностью не менее 10-5. Если искомой гомотетии не существует, необходимо вывести в выходной файл слово «NO».
3 -1 1 1 1 1 5 1 9 -3 1 1 1
YES 1.0 1.0 2.0
3 -1 1 1 1 1 5 1 1 0 0 1 0
NO