Темы
    Информатика(2656 задач)
---> 109 задач <---
Источники --> Личные олимпиады --> Всероссийская олимпиада школьников --> Региональный этап
    2009(8 задач)
    2010(8 задач)
    2011(8 задач)
    2012(8 задач)
    2013(8 задач)
    2014(8 задач)
    2015(8 задач)
    2016(8 задач)
    2017(8 задач)
    Московская областная олимпиада(13 задач)
    Кировская открытая областная олимпиада(21 задач)
    Санкт-Петербург(3 задач)
Страница: << 7 8 9 10 11 12 13 >> Отображать по:
#3140
Феодальные отношения
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

Во Флатландии с некоторых пор процветают феодальные отношения – у каждого порядочного феодала есть ровно два вассала, у непорядочных – вассалов нет совсем. Каждый феодал строит свой замок в городе на прямой, при этом:

  • высота замка (всегда целое положительное число) должна быть строго больше высот замков его вассалов (для соблюдения субординации).
  • замки первого из двух вассалов и всех вассалов этого вассала должны быть построены слева, второго вассала и его вассалов – справа (для пресечения междоусобиц). Это правило должно выполняться для всех
  • высота замка должна быть минимально возможной (для экономии ресурсов)
  • число всех подчиненных (непосредственно или через промежуточных) у правого и левого вассалов одинаково (для баланса сил).

Для удобства замки феодалов занумерованы натуральными числами по порядку слева направо, начиная с единицы, и разбиты на улицы. Улица (i, j) представляет собой последовательность подряд идущих замков, начиная с замка под номером i и заканчивая замком с номером j (i ≤ j)

Однажды в город приехал новый феодал и пожелал выкупить там замок у одного из жителей. Также ему стало интересно узнать социальный статус соседей по улице, однако, город к тому времени так разросся, что феодал уже не мог сделать этого самостоятельно. Напишите программу, которая поможет ему!

Входные данные

Первая строка входного файла содержит число N (1 ≤ N ≤ 30000) — высота замка единственного главного феодала в городе, который никому не подчиняется. Далее, в следующих двух строках идут числа i и j (\(0 \leq i, j < 10^{10000}\)), задающие улицу (i, j), на которой хочет приобрести замок новый феодал (гарантируется, что замки с номерами i и j находятся в черте города, i ≤ j, j – i ≤ 105).

В выходной файл требуется вывести высоты всех замков на указанной улице слева направо через пробел.

Примечание

Будут оцениваться и частичные решения задачи при малых N. Частичные решения для N<20 набирают до 40 баллов, а для N<50 набирают не более 70 баллов.

Ввод
Вывод
2
1
3
1 2 1
3
3
7
1 3 1 2 1
50
128873293
128873293
1
#3141
iCopter
  

В двухмерной игре для современных мобильных телефонов «iCopter» между Васей и Петей идет Bluetooth-сражение. Идет третий раунд. Он проходит с применением вертолётной техники в горном массиве.

Горный профиль в игре «iCopter» задается ломаной (x1, y1), (x2, y2), …, (xN, yN), координаты вершин которой удовлетворяют неравенствам x1 < x2 < … < xN. Начальные и конечные точки профиля расположены на уровне моря (y1 = yN = 0).

Над горами летают вертолет Васи и вертолет Пети. Вертолёт Васи находится в точке A с координатами (XA, YA), Пети — в точке B с координатами (XB, YB). Вертолет Васи производит выстрел снарядом с начальной скоростью, которая задается вектором с компонентами (VX , VY).

Полёт снаряда проходит по следующим законам движения (они определяют координаты снаряда в каждый момент времени до столкновения с горой t ≥ 0):

X = XA + VX * t

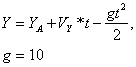
В данной версии компьютерной игры снаряд взрывается только от удара в гору. При взрыве снаряд поражает все цели на расстоянии не больше R от эпицентра взрыва. Вертолёт противника считается уничтоженным, если он находится в радиусе поражения.

Требуется написать программу, которая по заданному рельефу, скорости снаряда и координатам вертолётов определяет точку попадания снаряда в гору и уничтожен ли при этом вертолёт Пети.

Входные данные

В первой строке входного файла задается семь целых чисел – радиус поражения R (0 ≤ R≤ 10 000, координаты точки A, координаты точки B, компоненты вектора скорости снаряда VX, VY ( -104 ≤ VX≤ 104, VX ≠ 0, 0 < VY≤ 104). Точки Aи B различны.

Во второй строке находится натуральное число N – количество вершин ломаной (2 ≤ N≤ 100 000), которая задает горный профиль. Последующие N строк содержат координаты вершин ломаной (x1, y1), (x2, y2), …, (xN, yN).

Координаты вершин ломаной, а также точек A и B, задаются парой целых чисел, не превосходящих по абсолютному значению 106. Гарантируется, что x1 < x2 < … < xN и y1 = yN = 0, а также то, что снаряд всегда попадает в заданный горный профиль и координата точки попадания xП по оси X лежит в пределах
x1 ≤ xП ≤ xN­­.

Выходные данные

В первой строке выведите координаты точки взрыва с точностью не менее 3 знаков после запятой. Во второй строке выведите «YES», если вертолёт Пети будет поражен взрывом, и «NO» в противном случае.

Ввод
Вывод
4 6 6 0 6 -4 4
3
0 0
3 11
6 0
4.150749 6.780586
NO
4 6 6 1 6 -4 4
3
0 0
3 11
6 0
4.150749 6.780586
YES
#3142
Автозаправки
  

Фирма «АйОйЛ» построила на скоростном шоссе Москва-Тверь N автозаправок. Каждая автозаправка имеет свой номер, который присваивался ей при строительстве, начиная с единицы. Кроме того, каждая автозаправка располагается на определенном километре шоссе. Километры на шоссе нумеруются от 0, начиная от Москвы.

Экономические расчеты показали нецелесообразность наличия на данном шоссе такого количества автозаправок, поэтому требуется сократить одну из них. Для максимального удобства автомобилистов необходимо закрыть такую автозаправку, которая  имеет минимальное расстояние вдоль шоссе до ближайшей к ней другой автозаправки.

Требуется написать программу, которая находит автозаправку, которую можно сократить.

Входные данные

Первая строка входного файла содержит количество автозаправок N (2 ≤ N ≤ 105). Вторая строка входного файла содержит N различных целых чисел xi – километр, на котором расположена автозаправка с номером i (1 ≤ i ≤ N). Числа в строке разделены пробелом. Значения всех xi не меньше ноля и не  превосходят 109 по абсолютной величине.

Выходные данные

В первой строке выходного файла необходимо вывести номер автозаправки, которую можно сократить. Если ответов несколько, выведите любой из них.

Ввод
Вывод
5
10 3 7 2 5
4
#3143
Перевес багажа
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

Впервые в жизни Петя летит на международную олимпиаду по программированию. Петя так волновался, что взял с собой множество вещей и теперь во время регистрации на рейс его чемодан не принимают, так как у него превышение разрешенной массы багажа.

У Пети в чемодане лежат N предметов, каждый предмет имеет свой вес Wi килограмм и ценность Ai рублей, причем оказалось так, что для любого предмета выполняется следующее неравенство:

W1 + W2 + … + Wi-1 ≤ Wi

Пете сообщили, что у него перевес чемодана в M килограмм, поэтому ему придется оставить в аэропорту какие-то предметы с суммарной массой не меньше M. При этом Петя хочет понести минимальный урон, а поэтому оставленные предметы должны иметь наименьшую возможную стоимость.

Требуется написать программу, которая подсчитает минимальную возможную стоимость оставленных предметов.

Входные данные

В первой строке задаётся количество предметов в багаже у Пети N (1 ≤ N ≤ 50) и какой у Пети перевес чемодана в килограммах M (1 ≤ M ≤ 1018). Во второй строке задаются N целых неотрицательных чисел – вес всех вещей Wi, сумма чисел не превышает 1018. В третьей строке заданы N целых неотрицательных чисел – ценность всех вещей Ai , все числа не превышают 109.

Выходные данные

В выходной файл требуется вывести минимальную суммарную стоимость предметов, которые Петя будет вынужден оставить в аэропорту.

Ввод
Вывод
4 15
5 10 15 30
1 5 3 6
3
3 2
1 2 4
7 6 5
5
#3144
ASCII-art
  
ASCII art (от англ. ASCII artwork) — форма изобразительного искусства, использующая символы ASCII на моноширинном экране компьютерного терминала (или принтера) для представления изображений. При создании такого изображения используется палитра, состоящая из буквенных, цифровых символов и символов знаков пунктуации.

Википедия

Флатландия – необычная страна, и искусство у флатландцев тоже необычное. Особый интерес представляют их картины. Во-первых, флатландские художники используют для написания картин только ASCII символы, во-вторых, все картины исключительно квадратные.

Пете захотелось приобщиться к искусству Флатландии, однако, он столкнулся с очень серьёзной проблемой. Дело в том, что все картины защищены законом об авторских правах и кодируются следующим образом: над картиной последовательно выполняются K операций. Каждая операция – одно из четырёх зеркальных отражений:

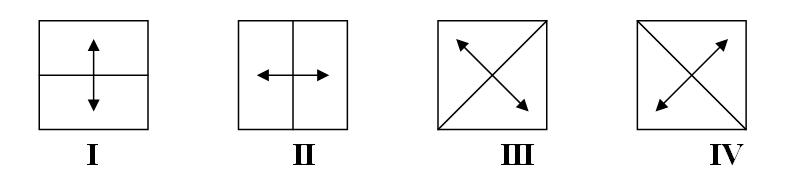
Operations with image
  • Ось отражения – горизонтальная прямая, делящая изображение пополам. При отражении первая строка меняется местами с последней, вторая – с предпоследней и т.д.
  • Ось отражения – вертикальная прямая, делящая изображение пополам. При отражении первый столбец меняется местами с последним, второй – с предпоследним и т.д.
  • Ось отражения – побочная диагональ (диагональ, соединяющая правый верхний и левый нижний угол изображения). При отражении левый верхний угол меняется с правым нижним и т. д.
  • Ось отражения – главная диагональ (диагональ, соединяющая левый верхний и правый нижний угол изображения). При отражении правый верхний угол меняется с левым нижним и т. д.

Из надёжных источников Пете удалось узнать, какие отражения применялись к картине. Требуется написать программу, которая поможет ему раскодировать изображение.

Входные данные

В первой строке входного файла находятся два натуральных числа N и K (1 ≤ N ≤ 1000, 1 ≤ K ≤ 1000000), где N – размер картины, K – число отражений, применяемых для кодирования. Во второй строке содержатся K натуральных чисел, обозначающих номера отражений (числа могут принимать только значения 1, 2, 3 или 4).

В следующих N строках описывается само закодированное изображение. В (i+2)-й строке записана i-я строка закодированной картины. В изображении используются символы с ASCII-кодами от 32 до 126 включительно.

Выходные данные

В выходной файл требуется вывести раскодированное изображение.

Ввод
Вывод
5 1 
1
UVWXY
PQRST
KLMNO
FGHIJ
ABCDE
ABCDE
FGHIJ
KLMNO
PQRST
UVWXY
7 8 
1 3 1 2 4 1 2 3
RQZQQWD
MFSUWDS
YODIIKO
KNECWHT
YRQZQQW
NMFSUWD
SYODIIK
DSOTWDK
WDKHQWI
QWIWQUI
QUICZSD
ZSDEQFO
QFONRMY
RMYKYNS
11 2
1 4 
[/|  ||   .
_=~||_ _   
]\ |||||   
_ \_   _/  
[/__  =_ _ 
_=_*OO=_(_ 
]\__  =_)_ 
_ /_   _\  
[/ |||||   
_=~||_ _   
]\|  ||   .
.         .
    ___    
   / ()\   
 _|_____|_ 
| | === | |
|_|  O  |_|
 ||  O  || 
 ||__*__|| 
|~ \___/ ~|
/=\ /=\ /=\
[_]_[_]_[_]
36 7
1 3 4 2 4 2 1 
 |||||||||||||||||||||||||||||||||| 
-                                  -
-                                  -
-                                  -
-                                  -
-                                  -
-                 &  &,   &        -
-             &   7&~BM   M#6      -
-             M    4M_M    MM&g    -
-         !#8&@     M M    M_MM    -
-         *]44Q     M #    M8Mj    -
-             M   MMMMM   !Mj      -
-             *           *        -
-                                  -
-                                  -
-                                  -
-                                  -
-                                  -
-                                  -
-               r   g         6    -
-     ^        ^    ^  FMg`X  M&   -
-^&#&\(# ~    f ~    ~  _7M "  B00c -
-~MMMMN ~MMMMM ^    ~    M_ _  "#M&-
-~    " ~]]]]M ~g   #  , M& _  ^ Mj-
-               M&8#g  N "0#   ^!  -
-               "0M0          Ej   -
-                 ]           _    -
-                                  -
-                                  -
-                                  -
-                                  -
-                                  -
-                                  -
-                                  -
-                                  -
 ||||||||||||||||||||||||||||||||||
----------------------------------
|           j&                     |
|           MMc                    |
|          ! #0                    |
|         j^^"0&                   |
|        _E   BM6        jMg       |
|                        MM&       |
|           __          j8_M6      |
|          #  "X        MMMM#      |
|          0&_ `       *!   M&     |
|          "MMMg                   |
|             7M                   |
|          N, _F                   |
|                       M#MMM,     |
|                       M  _B&     |
|          g#~~^g       MMMM~      |
|         0#            M  4&      |
|        ]M8            M   7&     |
|         0&                       |
|         "Mg   r                  |
|           ~^~^                   |
|                      *MQ@M&      |
|           MMf          4&        |
|           ]M           48        |
|           ]M           ]#        |
|           ]M           *!        |
|           ]M                     |
|           ~~~                    |
|                                  |
|           "N#^                   |
|            M\)                    |
|            M&                    |
|            M#                    |
|            M&                    |
|           ~~^                    |
 ----------------------------------
Страница: << 7 8 9 10 11 12 13 >> Отображать по:
Выбрано
:
Отменить
|
Добавить в контест