Миша уже научился хорошо фотографировать и недавно увлекся программированием. Первая программа, которую он написал, позволяет формировать негатив чёрно-белого изображения.

Бинарное чёрно-белое изображение — это прямоугольник, состоящий из пикселей, каждый из которых может быть либо чёрным, либо белым. Негатив такого изображения получается путём замены каждого чёрного пикселя на белый, а каждого белого пикселя — на чёрный.

Миша, как начинающий программист, написал свою программу с ошибкой, поэтому в результате её исполнения мог получаться некорректный негатив. Для того чтобы оценить уровень несоответствия получаемого негатива исходному изображению, Миша начал тестировать свою программу.

В качестве входных данных он использовал исходные изображения. Сформированные программой негативы он начал тщательно анализировать, каждый раз определяя число пикселей негатива, которые получены с ошибкой.

Требуется написать программу, которая в качестве входных данных использует исходное бинарное чёрно-белое изображение и полученный Мишиной программой негатив, и на основе этого определяет количество пикселей, в которых допущена ошибка.

С детства Максим был неплохим музыкантом и мастером на все руки. Недавно он самостоятельно сделал несложный перкуссионный музыкальный инструмент — треугольник. Ему нужно узнать, какова частота звука, издаваемого его инструментом.

У Максима есть профессиональный музыкальный тюнер, с помощью которого можно проигрывать ноту с заданной частотой. Максим действует следующим образом: он включает на тюнере ноты с разными частотами и для каждой ноты на слух определяет, ближе или дальше она к издаваемому треугольником звуку, чем предыдущая нота. Поскольку слух у Максима абсолютный, он определяет это всегда абсолютно верно.

Вам Максим показал запись, в которой приведена последовательность частот, выставляемых им на тюнере, и про каждую ноту, начиная со второй, записано — ближе или дальше она к звуку треугольника, чем предыдущая нота. Заранее известно, что частота звучания треугольника Максима составляет не менее 30 герц и не более 4000 герц.

Требуется написать программу, которая определяет, в каком интервале может находиться частота звучания треугольника.

Предприятие «Авто-2010» выпускает двигатели для известных во всём мире автомобилей. Двигатель состоит ровно из \(n\) деталей, пронумерованных от 1 до \(n\), при этом деталь с номером \(i\) изготавливается за \(p_i\) секунд. Специфика предприятия «Авто-2010» заключается в том, что там одновременно может изготавливаться лишь одна деталь двигателя. Для производства некоторых деталей необходимо иметь предварительно изготовленный набор других деталей.

Генеральный директор «Авто-2010» поставил перед предприятием амбициозную задачу — за наименьшее время изготовить деталь с номером 1, чтобы представить её на выставке.

Требуется написать программу, которая по заданным зависимостям порядка производства между деталями найдёт наименьшее время, за которое можно произвести деталь с номером 1.

В наши дни предоставление поверхностей заборов и стен промышленных зданий рекламодателям — уже не оригинальный способ получить дополнительный заработок, а нечто само собой разумеющееся.

Небольшая компания «Домострой» также решила выйти на этот рынок и стала предлагать место для рекламы на своих блоках заборов. Блок представляет собой параллелепипед размером \(1\times1\times L\), на одной из сторон которого есть место для рекламы — пространство размера \(1\times L\), в которое можно вписать ровно \(L\) букв латинского алфавита.

К сожалению, иногда сделки у компании срывались, и заранее подготовленные блоки с рекламой отправлялись на склад. Со временем там скопилось приличное количество блоков различных типов (блоки разных типов отличаются друг от друга только надписью), поэтому было решено использовать их вторично.

Была предложена следующая идея: если поставить несколько блоков друг на друга и закрасить ненужные буквы, то, читая сверху вниз и слева направо, можно будет прочитать какой-нибудь другой текст, как показано на рисунке.

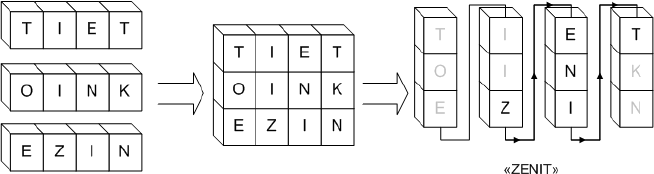
После того, как некоторое число \(K\) блоков, каждый из которых имеет длину \(L\), поставили друг на друга, получилась прямоугольная таблица размером \(K\times L\), в каждой клетке которой находится буква латинского алфавита. Каждый рекламный блок соответствует строке этой таблицы. Теперь содержимое этой таблицы выписывается по столбцам, начиная с самого левого. При этом в каждом столбце буквы выписываются сверху вниз. В случае, изображённом на рисунке, в результате этого процесса получилась бы строка «TOEIIZENITKN». Необходимо, чтобы рекламная надпись, требуемая заказчику, входила в получившуюся строку как подстрока «TOEIIZENITKN».

Требуется написать программу, которая будет определять, какое минимальное количество блоков надо использовать, чтобы получить рекламную надпись, необходимую заказчику. При этом можно считать, что на складе блоков каждого типа неограниченно много.