Победитель школьного этапа олимпиады по информатике нашел дома в старых бумагах результаты чемпионата страны по стрельбе из лука, в котором участвовал его папа. К сожалению, листок с результатами сильно пострадал от времени, и разобрать фамилии участников было невозможно. Остались только набранные каждым участником очки, причем расположились они в том порядке, в котором участники чемпионата выполняли стрельбу.
Расспросив папу, школьник выяснил, что количество очков, которое набрал папа, заканчивается на 5, один из победителей чемпионата стрелял раньше, а папин друг, который стрелял сразу после папы, набрал меньше очков. Теперь он заинтересовался, какое самое высокое место мог занять его папа на том чемпионате.
Будем считать, что участник соревнования занял \(k\)-е место, если ровно \((k - 1)\) участников чемпионата набрали строго больше очков, чем он. При этом победителями считались все участники чемпионата, занявшие первое место.
Требуется написать программу, которая по заданным результатам чемпионата определяет, какое самое высокое место на чемпионате мог занять папа победителя школьного этапа олимпиады по информатике.
Выходные данные
В выходном файле должно содержаться одно целое число — самое высокое место, которое мог занять папа школьника. Если не существует ни одного участника чемпионата, который удовлетворяет, описанным выше условиям, выведите в выходной файл число 0.
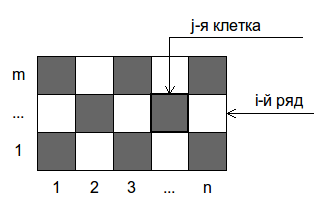 Аня разделила доску размера \(m \times n\) на клетки размера \(1 \times 1\) и раскрасила их в черный и белый цвет в шахматном порядке. Васю заинтересовал вопрос: клеток какого цвета получилось больше — черного или белого.
Аня разделила доску размера \(m \times n\) на клетки размера \(1 \times 1\) и раскрасила их в черный и белый цвет в шахматном порядке. Васю заинтересовал вопрос: клеток какого цвета получилось больше — черного или белого.